2024年高考数学第一轮复习精品导学案第65讲 双曲线的标准方程与性质（学生版）+教师版

这是一份2024年高考数学第一轮复习精品导学案第65讲 双曲线的标准方程与性质（学生版）+教师版，共2页。学案主要包含了 双曲线的定义等内容，欢迎下载使用。
一、 双曲线的定义
平面内与两个定点F1，F2的 (小于eq \b\lc\|\rc\|(\a\vs4\al\c1(F1F2)))的点的轨迹叫做双曲线．这两个定点叫做双曲线的 ，两焦点间的距离叫做双曲线的 ．
集合P＝{Meq \b\lc\|\rc\|(\a\vs4\al\c1(\b\lc\|\rc\ (\a\vs4\al\c1(\b\lc\|\rc\|(\a\vs4\al\c1(MF1))))－\b\lc\|\rc\|(\a\vs4\al\c1(MF2))))＝2a}，eq \b\lc\|\rc\|(\a\vs4\al\c1(F1F2))＝2c，其中a，c为常数，且a>0，c>0.
(1)当a＜c时，点P的轨迹是 ；
(2)当a＝c时，点P的轨迹是 ；
(3)当a＞c时，点P ．
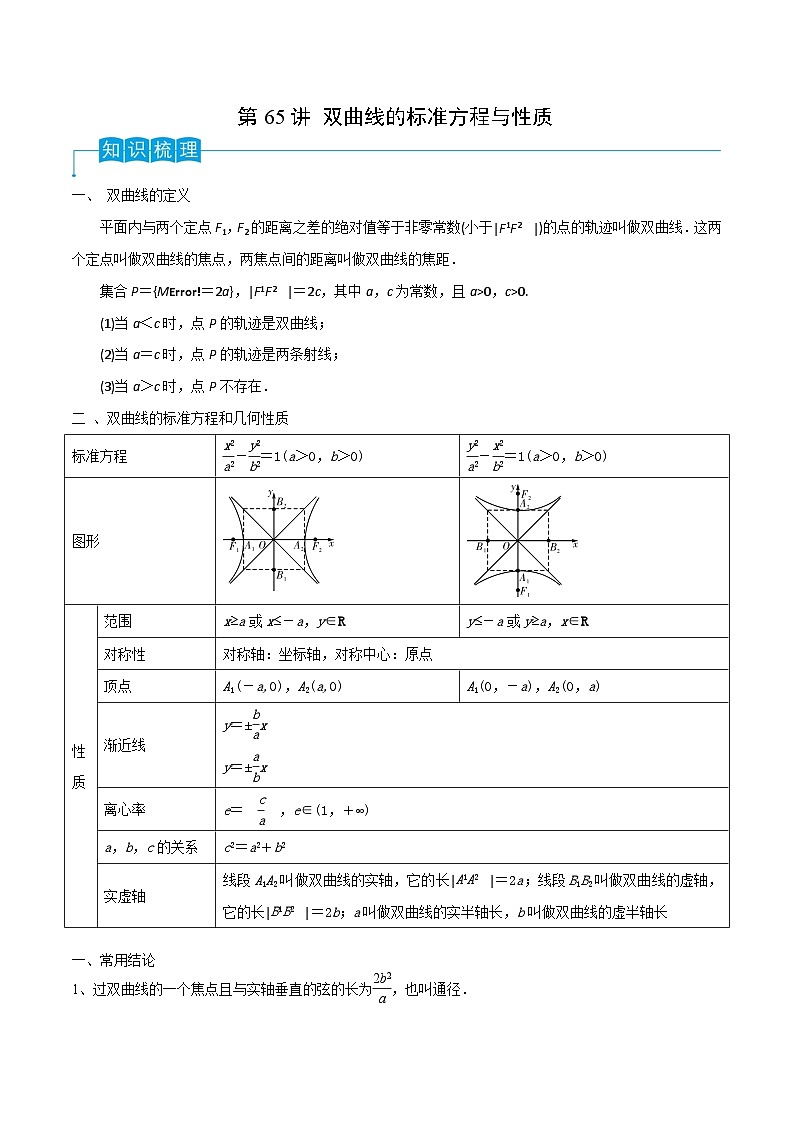
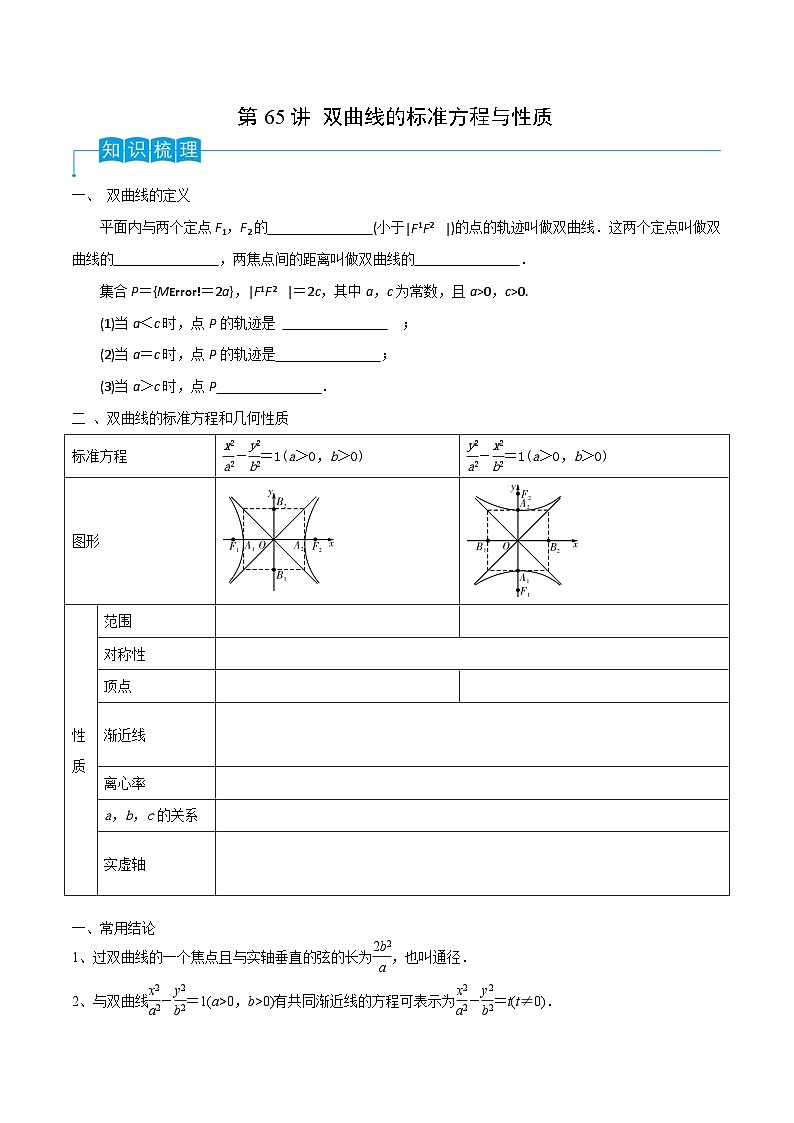
二 、双曲线的标准方程和几何性质
常用结论
1、过双曲线的一个焦点且与实轴垂直的弦的长为eq \f(2b2,a)，也叫通径．
2、与双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)有共同渐近线的方程可表示为eq \f(x2,a2)－eq \f(y2,b2)＝t(t≠0)．
3、双曲线的焦点到其渐近线的距离为b.
4、若P是双曲线右支上一点，F1，F2分别为双曲线的左、右焦点，则|PF1|min＝a＋c，|PF2|min＝c－a.
1、（2023•乙卷（文））设，为双曲线上两点，下列四个点中，可为线段中点的是
A．B．C．D．
2、（2021•甲卷（文））点到双曲线的一条渐近线的距离为
A．B．C．D．
3、（2023•天津）双曲线的左、右焦点分别为，．过作其中一条渐近线的垂线，垂足为．已知，直线的斜率为，则双曲线的方程为
A．B．C．D．
4、（2023•北京）已知双曲线的焦点为和，离心率为，则的方程为 ．
5、（2021•新高考Ⅱ）已知双曲线的离心率，则该双曲线的渐近线方程为 ．
6、（2021•乙卷（理））已知双曲线的一条渐近线为，则的焦距为 ．
7、（2021•乙卷（文））双曲线的右焦点到直线的距离为 ．
8、【2020年新课标1卷文科】设是双曲线的两个焦点，为坐标原点，点在上且，则的面积为（ ）
A．B．3C．D．2
9、【2020年新课标3卷理科】设双曲线C：（a>0，b>0）的左、右焦点分别为F1，F2，离心率为．P是C上一点，且F1P⊥F2P．若△PF1F2的面积为4，则a=（ ）
A．1B．2C．4D．8
1、双曲线 eq \f(x2,3)－ eq \f(y2,2)＝1的焦距为( )
A. 5 B. eq \r(5)
C. 2 eq \r(5) D. 1
2、已知双曲线C： eq \f(x2,a2)－ eq \f(y2,b2)＝1(a>0，b>0)的焦距为 2 eq \r(5)，点P(2，1)在双曲线C的一条渐近线上，则双曲线C的方程为( )
A. x2－ eq \f(y2,4)＝1 B. eq \f(x2,4)－y2＝1
C. eq \f(3x2,20)－ eq \f(3y2,5)＝1 D. eq \f(x2,16)－ eq \f(y2,4)＝1
3、设P是双曲线eq \f(x2,16)－eq \f(y2,20)＝1上一点，F1，F2分别是双曲线的左、右焦点，若|PF1|＝9，则|PF2|等于( )
A．1 B．17
C．1或17 D．以上均不对
4、已知方程eq \f(x2,1＋k)－eq \f(y2,1－k)＝1表示双曲线，则k的取值范围是（ ）
A． B． C． D．
5、 中心在坐标原点，离心率为eq \f(5,3)的双曲线的焦点在y轴上，则它的渐近线方程为（ ）
A． B． C． D．
6、在平面直角坐标系xOy中，已知椭圆C1与双曲线C2共焦点，双曲线C2实轴的两顶点将椭圆C1的长轴三等分，两曲线的交点与两焦点共圆，则双曲线C2的离心率为________．
考向一 双曲线的定义
例1 (1)已知定点F1(－2,0)，F2(2,0)，N是圆O：x2＋y2＝1上任意一点，点F1关于点N的对称点为M，线段F1M的中垂线与直线F2M相交于点P，则点P的轨迹是( )
A．椭圆 B．双曲线
C．抛物线 D．圆
(2)(2022·滨州质检)eq \r(x2＋（y－3）2)－eq \r(x2＋（y＋3）2)＝4表示的曲线方程为( )
A.eq \f(x2,4)－eq \f(y2,5)＝1(x≤－2)
B.eq \f(x2,4)－eq \f(y2,5)＝1(x≥2)
C.eq \f(y2,4)－eq \f(x2,5)＝1(y≤－2)
D.eq \f(y2,4)－eq \f(x2,5)＝1(y≥2)
变式、已知圆C1：(x＋3)2＋y2＝1和圆C2：(x－3)2＋y2＝9，动圆M同时与圆C1及圆C2相外切，则动圆圆心M的轨迹方程为________________.
方法总结：(1)利用双曲线的定义判定平面内动点与两定点的轨迹是否为双曲线，进而根据要求可求出双曲线方程．
(2)在“焦点三角形”中，常利用正弦定理、余弦定理，经常结合||PF1|－|PF2||＝2a，运用平方的方法，建立为|PF1|·|PF2|的关系．
(3)在运用双曲线的定义解题时，应特别注意定义中的条件“差的绝对值”，弄清楚是指整条双曲线还是双曲线的一支．
考向二 双曲线的标准方程
例2、根据下列条件，求双曲线的标准方程：
(1) 虚轴长为12，离心率为 eq \f(5,4)；
(2) 焦距为26，且经过点M(0，12)；
(3) 经过点P(－3，2 eq \r(7))和点Q(－6 eq \r(2)，－7)；
(4) 焦点在x轴上，焦距为10，与双曲线 eq \f(y2,4)－x2＝1有相同的渐近线．
变式、(1)已知双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的左焦点为F，离心率为eq \r(2).若经过F和P(0，4)两点的直线平行于双曲线的一条渐近线，则双曲线的方程为____．
(2)与双曲线eq \f(x2,9)－eq \f(y2,16)＝1有共同的渐近线，且经过点(－3，2eq \r(3))的双曲线的标准方程为___．
方法总结:求双曲线标准方程的一般方法
(1)待定系数法：设出双曲线方程的标准形式，根据已知条件，列出参数a，b，c的方程并求出a，b，c的值．与双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1有相同渐近线时，可设所求双曲线方程为eq \f(x2,a2)－eq \f(y2,b2)＝λ(λ≠0)．
(2)定义法：依定义得出距离之差的等量关系式，求出a的值，由定点位置确定c的值．
考向三 双曲线的性质
例3、已知双曲线的中心在原点，焦点在x轴上，一条渐近线方程是y＝ eq \f(2,3)x，两准线间的距离为18，求双曲线的方程．
变式1、（1）(2022·江苏第一次百校联考)双曲线(a＞0，b＞0)的左顶点为A，右焦点为F，动点B在双曲线C上．当BF⊥AF时，|AF|＝|BF|，则双曲线C的渐近线方程为 ▲ ．
（2）(2022·江苏海安中学期初)从某个角度观察篮球(如图1)，可以得到一个对称的平面图形，如图2所示，篮球的外轮形为圆O，将篮球表面的粘合线看成坐标轴和双曲线，若坐标轴和双曲线与圆O的交点将圆O的周长八等分，AB＝BC＝CD，则该双曲线的离心率为
A．eq \r(,2) B．eq \f(\r(,6),2) C．eq \f(3\r(,5),5) D．eq \f(4\r(,7),7)
A
D
C
O
B
图1 图2
变式2、（1）已知F1，F2是双曲线 eq \f(x2,a2)－ eq \f(y2,b2)＝1(a>0，b>0)的两个焦点，以线段F1F2为边作正三角形MF1F2，若边MF1的中点P在双曲线上，则双曲线的离心率是________．
（2）(2022·苏州期初考试)已知点P为双曲线C：EQ \F(x\S(2),a\S(2))－\F(y\S(2),b\S(2))＝1(a＞0，b＞0)右支上一点，F1，F2分别为C的左，右焦点，直线PF1与C的一条渐近线垂直，垂足为H，若PF1＝4HF1，则该双曲线的离心率为
A．EQ \F(\R(,15),3) B．EQ \F(\R(,21),3) C．eq \f(5,3) D．eq \f(7,3)
（3）若双曲线eq \f(y2,a2)－eq \f(x2,b2)＝1(a>0，b>0)的渐近线的斜率大于eq \f(2\r(3),3)，则双曲线离心率的取值范围是( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(21),3)，＋∞)) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(\r(21),3)))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(\r(7),2)，＋∞)) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(1，\f(\r(7),2)))
（4）已知双曲线eq \f(x2,a2)－eq \f(y2,b2)＝1(a>0，b>0)的左、右焦点分别为F1，F2，点P在双曲线的右支上，且PF1＝4PF2，则双曲线的离心率e的最大值为________．
方法总结：求双曲线离心率或其取值范围的方法：
(1)直接求出a，c的值，利用离心率公式直接求解.
(2)列出含有a，b，c的齐次方程(或不等式)，借助于b2＝a2－c2消去b，转化为含有e的方程(或不等式)求解.
1、(2022·江苏如皋期初考试)双曲线的两个焦点为，，双曲线上一点P到的距离为11，则点P到的距离为（ ）
A．1B．21C．1或21D．2或21
2、(2022·江苏如皋期初考试)已知双曲线的中心为坐标原点，一条渐近线方程为，点在上，则的方程为( )
A．B．
C．D．
3、(2022·武汉部分学校9月起点质量检测)设双曲线eq E：x\s\up6(2)－\f(y\s\up6(2),3)＝1的左右焦点为F1，F2，左顶点为A，点M是双曲线E在第一象限内的一点，直线MF1交双曲线E的左支于点N，若NA∥MF2，则|MF2|＝
A．eq \f(7,4) B．eq \f(5,2) C．eq \f(8,3) D．eq \f(11,4)
4、(2022·湖南省雅礼中学开学考试)已知eq F\s\d(1)，F\s\d(2)是双曲线C的两个焦点，P为C上一点，且eq ∠F\s\d(1)PF\s\d(2)＝60°，eq |PF\s\d(1)|＝3|PF\s\d(2)|，则C的离心率为
A．eq \f(\r(,7),2) B．eq \f(\r(,13),2) C．eq \r(,7) D．eq \r(,13)
5、(2022·南京9月学情【零模】)在平面直角坐标系xOy中，双曲线C：eq \f(x\s\up6(2),a\s\up6(2))－\f(y\s\up6(2),b\s\up6(2))＝1(a＞0，b＞0)的左、右焦点分别为F1，F2，过F2且垂直于x轴的直线与C交于P，Q两点，F1Q与y轴的交点为R，F1Q⊥PR，则C的离心率为
A．eq \r(,2) B．eq \r(,3) C．2 D．eq \r(,5)
6、(2022·江苏如皋期初考试)已知双曲线右支上存在点P使得到左焦点的距离等于到右准线的距离的6倍，则双曲线的离心率的取值范围是 . 标准方程
eq \f(x2,a2)－eq \f(y2,b2)＝1(a＞0，b＞0)
eq \f(y2,a2)－eq \f(x2,b2)＝1(a＞0，b＞0)
图形
性质
范围
对称性
顶点
渐近线
离心率
a，b，c的关系
实虚轴