2024年高考数学第一轮复习精品导学案第83讲 变量间的相关关系、统计案例（教师版）+教师版

这是一份2024年高考数学第一轮复习精品导学案第83讲 变量间的相关关系、统计案例（教师版）+教师版，共2页。学案主要包含了2020年山东卷19，2020年海南卷19，小问1详解，小问2详解等内容，欢迎下载使用。
1. 变量间的相关关系
(1)常见的两变量之间的关系有两类：一类是函数关系，另一类是相关关系；与函数关系不同，相关关系是一种非确定性关系．eq \x(体现的不一定是因果关系.)
(2)从散点图上看，点散布在从左下角到右上角的区域内，两个变量的这种相关关系称为正相关；点散布在左上角到右下角的区域内，两个变量的这种相关关系为负相关．
2. 两个变量的线性相关
(1)从散点图上看，如果这些点从整体上看大致分布在通过散点图中心的一条直线附近，称两个变量之间具有线性相关关系，这条直线叫做回归直线．
(2)回归方程为y^＝b^x＋a^_，其中其中a^，b^是待定参数
(3)相关系数：
当r＞0时，表明两个变量正相关；
当r＜0时，表明两个变量负相关．
r的绝对值越接近于1，表明两个变量的线性相关性越强．r的绝对值越接近于0，表明两个变量之间几乎不存在线性相关关系．通常|r|大于0.75时，认为两个变量有很强的线性相关性．
3. 独立性检验
(1)2×2列联表
设X，Y为两个变量，它们的取值分别为{x1，x2}和{y1，y2}，其样本频数列联表(2×2列联表)如下：
(2)独立性检验
利用随机变量K2(也可表示为χ2)的观测值k＝eq \f(n（ad－bc）2,（a＋b）（c＋d）（a＋c）（b＋d）)(其中n＝a＋b＋
c＋d为样本容量)来判断“两个变量有关系”的方法称为独立性检验．
常用结论
(1)求解回归方程的关键是确定回归系数a^，b^，应充分利用回归直线过样本中心点 (x－，y－)．
(2)根据K2的值可以判断两个分类变量有关的可信程度，若K2越大，则两分类变量有关的把握越大．
(3)根据回归方程计算的b^值，仅是一个预报值，不是真实发生的值．
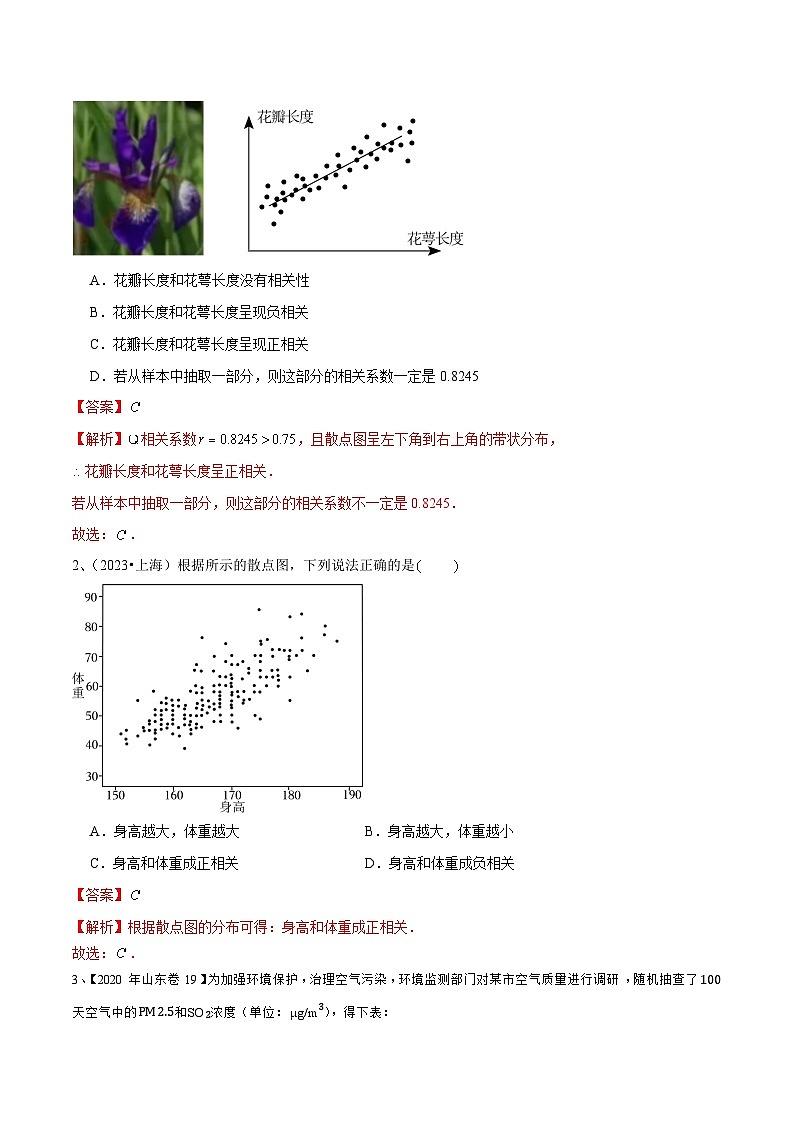
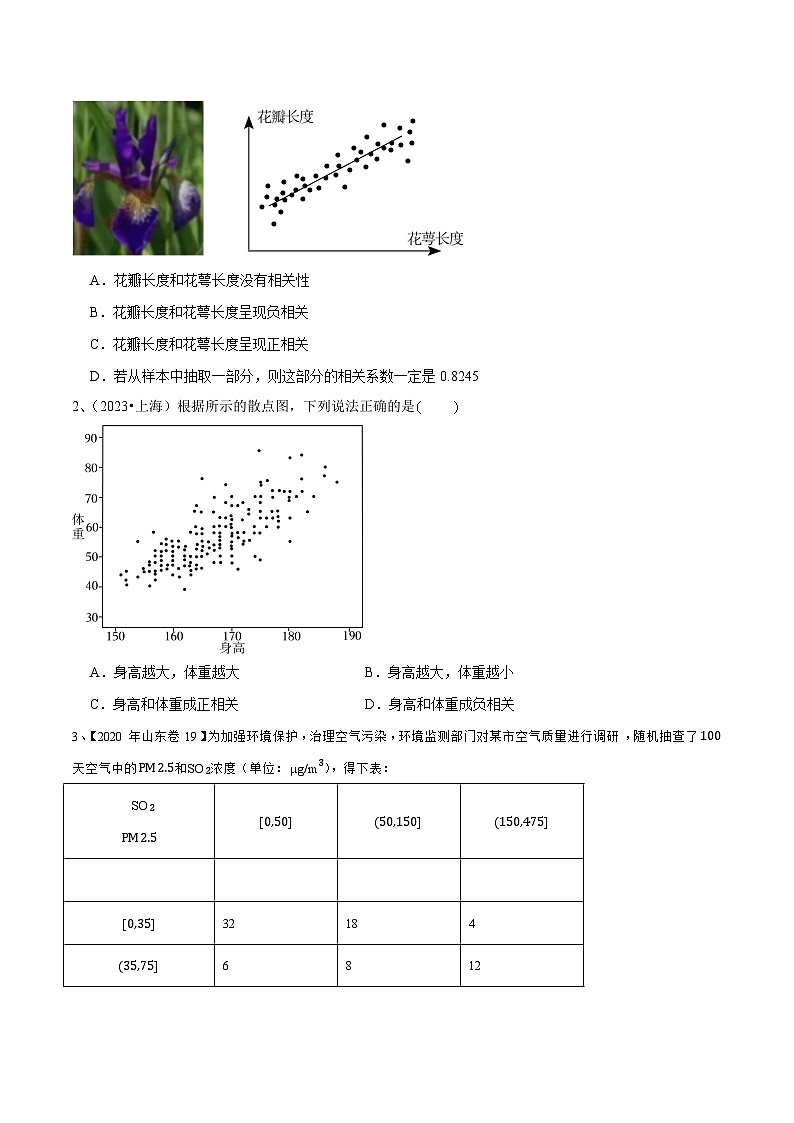
1、（2023•天津）调查某种花萼长度和花瓣长度，所得数据如图所示，其中相关系数，下列说法正确的是
A．花瓣长度和花萼长度没有相关性
B．花瓣长度和花萼长度呈现负相关
C．花瓣长度和花萼长度呈现正相关
D．若从样本中抽取一部分，则这部分的相关系数一定是0.8245
【答案】
【解析】相关系数，且散点图呈左下角到右上角的带状分布，
花瓣长度和花萼长度呈正相关．
若从样本中抽取一部分，则这部分的相关系数不一定是0.8245．
故选：．
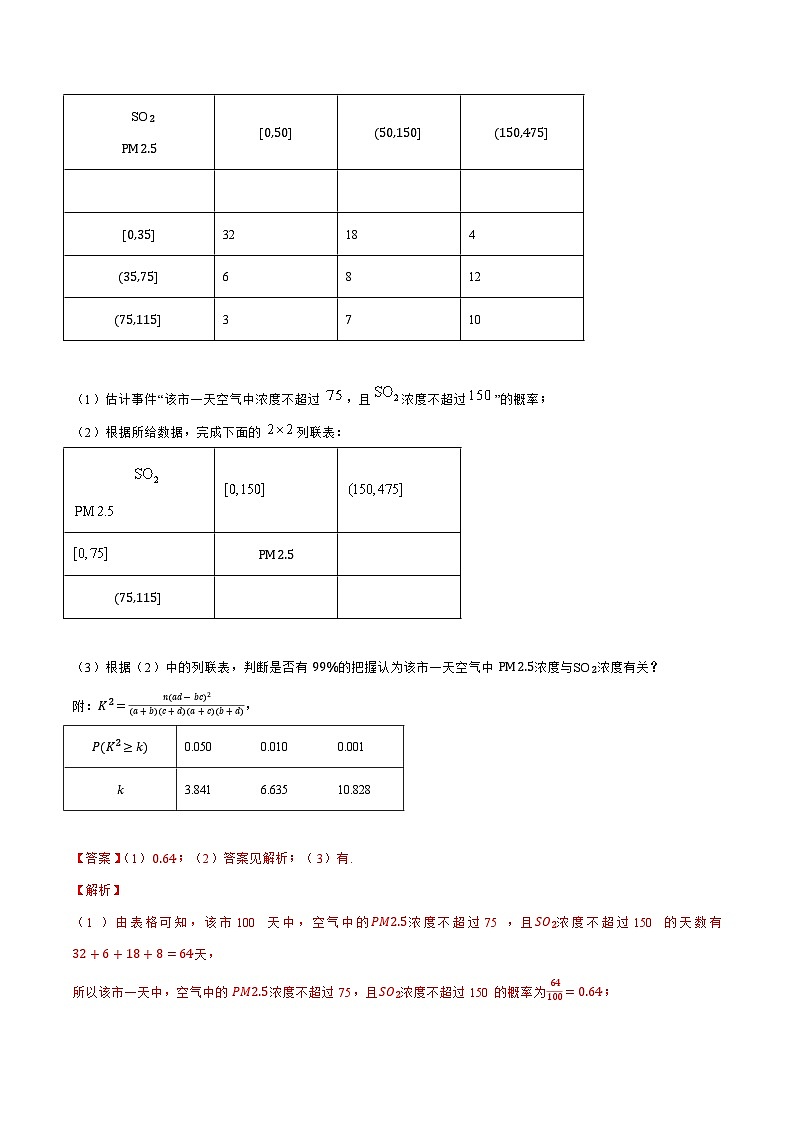
2、（2023•上海）根据所示的散点图，下列说法正确的是
A．身高越大，体重越大B．身高越大，体重越小
C．身高和体重成正相关D．身高和体重成负相关
【答案】
【解析】根据散点图的分布可得：身高和体重成正相关．
故选：．
3、【2020年山东卷19】为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的PM2.5和SO2浓度（单位：μg/m3），得下表：
（1）估计事件“该市一天空气中浓度不超过，且浓度不超过”的概率；
（2）根据所给数据，完成下面的列联表：
（3）根据（2）中的列联表，判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关？
附：K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)，
【答案】（1）0.64；（2）答案见解析；（3）有.
【解析】
（1）由表格可知，该市100天中，空气中的PM2.5浓度不超过75，且SO2浓度不超过150的天数有32+6+18+8=64天，
所以该市一天中，空气中的PM2.5浓度不超过75，且SO2浓度不超过150的概率为64100=0.64；
（2）由所给数据，可得2×2列联表为：
（3）根据2×2列联表中的数据可得
K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)=100×(64×10-16×10)280×20×74×26=3600481≈7.4844>6.635，
因为根据临界值表可知，有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
4、【2020年海南卷19】为加强环境保护，治理空气污染，环境监测部门对某市空气质量进行调研，随机抽查了100天空气中的PM2.5和SO2浓度（单位：μg/m3），得下表：
（1）估计事件“该市一天空气中PM2.5浓度不超过75，且SO2浓度不超过150”的概率；
（2）根据所给数据，完成下面的2×2列联表：
（3）根据（2）中的列联表，判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关？
附：K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)，
【答案】（1）0.64；（2）答案见解析；（3）有.
【解析】
（1）由表格可知，该市100天中，空气中的PM2.5浓度不超过75，且SO2浓度不超过150的天数有32+6+18+8=64天，
所以该市一天中，空气中的PM2.5浓度不超过75，且SO2浓度不超过150的概率为64100=0.64；
（2）由所给数据，可得2×2列联表为：
（3）根据2×2列联表中的数据可得
K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)=100×(64×10-16×10)280×20×74×26=3600481≈7.4844>6.635，
因为根据临界值表可知，有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关.
1、(2022·济宁二模)为研究变量x，y的相关关系，收集得到下面五个样本点(x，y)：
若由最小二乘法求得y关于x的回归直线方程为＝－1.8x＋，则据此计算残差为0的样本点是( )
A. (5，9) B. (6.5，8)
C. (7，6) D. (8，4)
【答案】 C
【解析】 由题意可知， eq \x\t(x)＝ eq \f(5＋6.5＋7＋8＋8.5,5)＝7， eq \x\t(y)＝ eq \f(9＋8＋6＋4＋3,5)＝6，所以回归方程的样本中心点为(7，6)，所以6＝－1.8×7＋，解得＝18.6，所以＝－1.8x＋18.6，在收集的5个样本点中，(7，6)一点在＝－1.8x＋18.6上，故计算残差为0的样本点是(7，6).
2、(2022·聊城一模)根据分类变量x与y的成对样本数据，计算得到χ2＝6.147.依据α＝0.01的独立性检验(P(χ2)≥6.635＝0.01)，结论为( )
A. 变量x与y不独立
B. 变量x与y不独立，这个结论犯错误的概率不超过0.01
C. 变量x与y独立
D. 变量x与y独立，这个结论犯错误的概率不超过0.01
【答案】 C
【解析】 按照独立性检验的知识及比对的参数值，当χ2＝6.147，我们可以下结论变量x与y独立．故排除选项A，B；因为6.147