2024年新高考数学一轮复习题型归纳与达标检测第28讲平面向量的概念及线性运算（讲）（Word版附解析）

这是一份2024年新高考数学一轮复习题型归纳与达标检测第28讲平面向量的概念及线性运算（讲）（Word版附解析），共6页。试卷主要包含了向量的有关概念，几种特殊向量，向量的线性运算，共线向量定理等内容，欢迎下载使用。

知识梳理
1．向量的有关概念
(1)向量的定义及表示：既有大小又有方向的量叫做向量．以A为起点、B为终点的向量记作eq \(AB,\s\up7(―→))，也可用黑体的单个小写字母a，b，c，…来表示向量．
(2)向量的长度(模)：向量eq \(AB,\s\up7(―→))的大小即向量eq \(AB,\s\up7(―→))的长度(模)，记为eq \(|AB|,\s\up7(―→)).
2．几种特殊向量
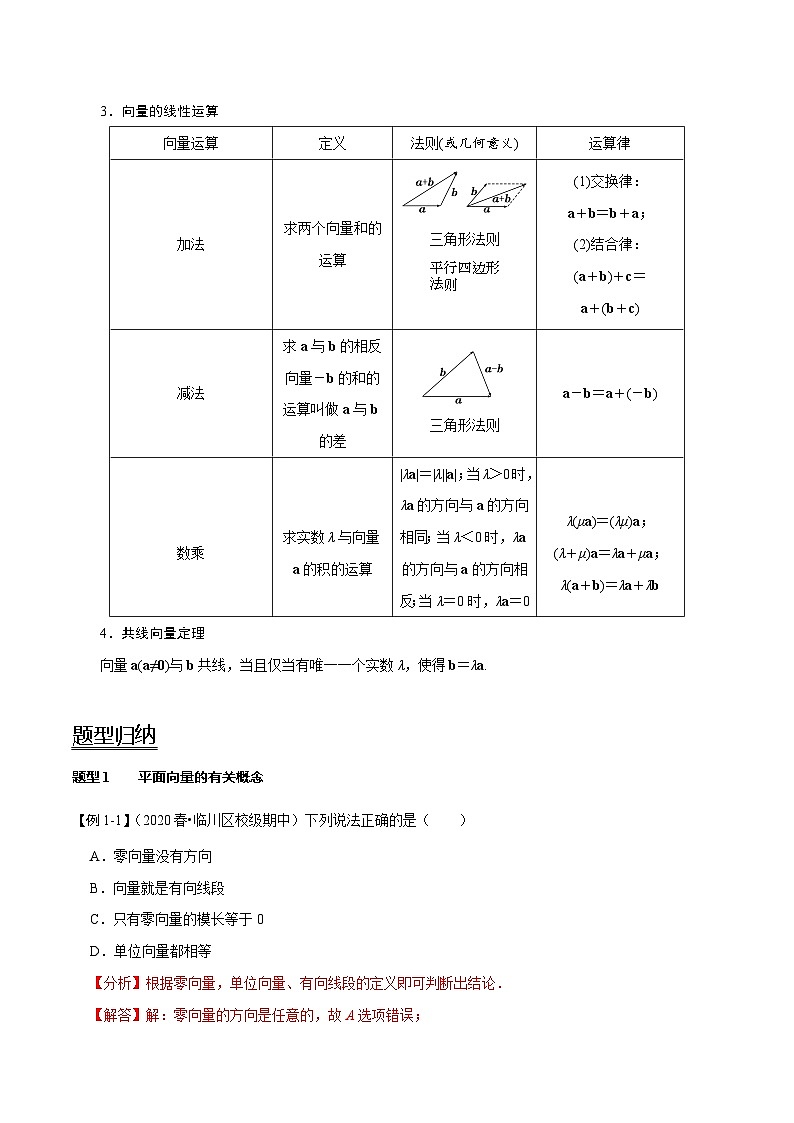
3．向量的线性运算
4．共线向量定理
向量a(a≠0)与b共线，当且仅当有唯一一个实数λ，使得b＝λa.
题型归纳
题型1 平面向量的有关概念
【例1-1】（2020春•临川区校级期中）下列说法正确的是（ ）
A．零向量没有方向
B．向量就是有向线段
C．只有零向量的模长等于0
D．单位向量都相等
【分析】根据零向量，单位向量、有向线段的定义即可判断出结论．
【解答】解：零向量的方向是任意的，故A选项错误；
有向线段只是向量的一种表示形式，两者不等同，故B选项错误；
只有零向量的模长等0，故C选项正确；
单位向量模长相等，单位向量若方向不同，则不是相等向量，故D选项错误．
故选：C．
【例1-2】（2020春•芮城县月考）有下列命题：
①两个相等向量，若它们的起点相同，终点也相同；
②若|a→|=|b→|，则a→=b→；
③若|AB→|=|DC→|，则四边形ABCD是平行四边形；
④若m→=n→，n→=k→，则m→=k→；
⑤若a→∥b→，b→∥c→，则a→∥c→；
⑥有向线段就是向量，向量就是有向线段．
其中，假命题的个数是（ ）
A．2B．3C．4D．5
【分析】根据平面向量的基本概念，对选项中的命题判断真假性即可．
【解答】解：对于①，两个相等向量时，它们的起点相同，则终点也相同，①正确；
对于②，若|a→|=|b→|，则a→、b→不一定相同，∴②错误；
对于③，若|AB→|=|DC→|，AB→、DC→不一定相等，
∴四边形ABCD不一定是平行四边形，③错误；
对于④，若m→=n→，n→=k→，则m→=k→，④正确；
对于⑤，若a→∥b→，b→∥c→，
当b→=0→时，a→∥c→不一定成立，∴⑤错误；
对于⑥，有向线段不是向量，向量可以用有向线段表示，∴⑥错误；
综上，假命题是②③⑤⑥，共4个．
故选：C．
【跟踪训练1-1】（2019春•城关区校级月考）给出下列命题：①零向量的长度为零，方向是任意的：②若a→，b→都是单位向量，则a→=b→；③向量AB→与BA→相等，则所有正确命题的序号是（ ）
A．①B．③C．①③D．①②
【分析】根据零向量和单位向量的定义，易知①正确②错误，由向量的表示方法可知③错误．
【解答】解：根据零向量的定义可知①正确；
根据单位向量的定义，单位向量的模相等，但方向可不同，故两个单位向量不一定相等，故②错误；
AB→与向量BA→互为相反向量，故③错误．
故选：A．
【跟踪训练1-2】（2019春•北碚区期末）下列命题中，正确的个数是（ ）
①单位向量都相等；
②模相等的两个平行向量是相等向量；
③若a→，b→满足|a→|＞|b→|且a→与b→同向，则a→＞b→；
④若两个向量相等，则它们的起点和终点分别重合；
⑤若a→∥b→，b→∥c→，则a→∥c→．
A．0个B．1个C．2个D．3个
【分析】根据平面向量的基本概念，对选项中的命题进行分析、判断正误即可．
【解答】解：对于①，单位向量的大小相等相等，但方向不一定相同，故①错误；
对于②，模相等的两个平行向量是相等向量或相反向量，故②错误；
对于③，向量是有方向的量，不能比较大小，故③错误；
对于④，向量是可以平移的矢量，当两个向量相等时，
它们的起点和终点不一定相同，故④错误；
对于⑤，b→=0→时，a→∥b→，b→∥c→，则a→与c→不一定平行．
综上，以上正确的命题个数是0．
故选：A．
【跟踪训练1-3】（2019•西湖区校级模拟）下列关于向量的叙述不正确的是（ ）
A．向量AB→的相反向量是BA→
B．模为1的向量是单位向量，其方向是任意的
C．若A，B，C，D四点在同一条直线上，且AB＝CD，则AB→=CD→
D．若向量a→与b→满足关系a→+b→=0→，则a→与b→共线
【分析】根据相反向量、单位向量的定义即可判断出选项A，B的叙述是正确的，根据共线向量基本定理即可判断选项D的叙述是正确的，从而叙述不正确的只能选C．
【解答】解：根据相反向量的定义即可判断选项A的叙述正确；根据单位向量的定义即可判断选项B的叙述正确；
AB→与CD→的方向不一定相同，从而得出AB→=CD→是错误的；a→+b→=0→，得出a→=-b→，得出a→与b→共线是正确的．
故选：C．
【跟踪训练1-4】（2019春•民乐县校级月考）下列关于向量的结论：
（1）若|a→|＝|b→|，则a→=b→或a→=-b→；
（2）向量a→与b→平行，则a→与b→的方向相同或相反；
（3）起点不同，但方向相同且模相等的向量是相等向量；
（4）若向量a→与b→同向，且|a→|＞|b→|，则a→＞b→．
其中正确的序号为（ ）
A．（1）（2）B．（2）（3）C．（4）D．（3）
【分析】根据向量的定义，平行向量和相等向量的定义判断即可．
【解答】解：根据向量的定义可判断（1）（4）错误，向量a→，b→都是零向量时，由向量a→，b→平行得不出方向相同或相反，从而判断（2）错误，根据相等向量的定义可判断（3）正确．
故选：D．
【名师指导】
向量有关概念的关键点
(1)向量定义的关键是方向和长度．
(2)非零共线向量的关键是方向相同或相反，长度没有限制．
(3)相等向量的关键是方向相同且长度相等．
(4)单位向量的关键是长度都是一个单位长度．
(5)零向量的关键是长度是0，规定零向量与任意向量共线．
题型2 向量的线性运算
【例2-1】（2020•海南）在△ABC中，D是AB边上的中点，则CB→=（ ）
A．2CD→+CA→B．CD→-2CA→C．2CD→-CA→D．CD→+2CA→
【分析】利用向量加法法则直接求解．
【解答】解：在△ABC中，D是AB边上的中点，
则CB→=CD→+DB→=CD→+AD→
=CD→+(AC→+CD→)
＝2CD→-CA→．
故选：C．
【例2-2】（2020•绥化模拟）已知点D在△ABC的边AC上，CD＝2DA，点E是BD中点，则EC→=（ ）
A．13AB→+23AC→B．12AB→+23AC→C．-13AB→+56AC→D．-12AB→+56AC→
【分析】根据条件可画出图形，可得出EC→=-12(CD→+CB→)，然后带人CD→=-23AC→，CB→=AB→-AC→，进行向量数乘运算即可得出答案．
【解答】解：如图，根据题意，
EC→=-12(CD→+CB→)=-12⋅(23CA→+AB→-AC→)=-12⋅(-23AC→-AC→+AB→)=-12AB→+56AC→．
故选：D．
【例2-3】（2020春•焦作期末）在正方形ABCD中，点M，N分别满足DM→=MC→，CN→=λNB→，且AD→-AB→=2NM→，则λ＝（ ）
A．2B．1C．12D．13
【分析】可画出图形，根据条件即可得出M为CD的中点，而根据AD→-AB→=2NM→可得出BD→=2NM→，从而得出N为BC的中点，从而得出CN→=NB→，从而得出λ的值．
【解答】解：如图，
∵DM→=MC→，∴M为CD的中点，
∵AD→-AB→=BD→=2NM→，
∴N为BC的中点，
∴CN→=NB→，
∴λ＝1．
故选：B．
【跟踪训练2-1】（2020春•凉山州期末）如图，△ABC中，已知CD→=2DB→，则AD→=（ ）
A．13AB→+23AC→B．34AB→+14AC→C．14AB→+34AC→D．23AB→+13AC→
【分析】根据条件可得出AD→-AC→=2(AB→-AD→)，然后根据向量的数乘运算解出向量AD→即可．
【解答】解：∵CD→=2DB→，
∴AD→-AC→=2(AB→-AD→)，
∴AD→=23AB→+13AC→．
故选：D．
【跟踪训练2-2】（2020•东莞市二模）已知A，B，C三点不共线，且点O满足16OA→-12OB→-3OC→=0→，则（ ）
A．OA→=12AB→+3AC→B．OA→=-12AB→+3AC→
C．OA→=12AB→-3AC→D．OA→=-12AB→-3AC→
【分析】把已知条件整理即可求解结论．
【解答】解：因为点O满足16OA→-12OB→-3OC→=0→，
故OA→+12OA→-12OB→+3OA→-3OC→=0→；
即：OA→+12BA→+3CA→=0→⇒OA→=12AB→+3AC→；
故选：A．
【跟踪训练2-3】（2020•湖北模拟）△ABC中，点D为BC的中点，AB→=3AE→，M为AD与CE的交点，若AM→=λAD→，则实数λ＝（ ）
A．14B．13C．25D．12
【分析】根据D为BC的中点可得出AD→=12AB→+12AC→，再根据AB→=3AE→即可得出AM→=3λ2AE→+λ2AC→，而根据E，M，C三点共线即可得出3λ2+λ2=1，解出λ即可．
【解答】解：如图，D为BC的中点，
∴AD→=12AB→+12AC→，
又∵AM→=λAD→，且AB→=3AE→，
∴AM→=λ2AB→+λ2AC→=3λ2AE→+λ2AC→，且E，M，C三点共线，
∴3λ2+λ2=1，解得λ=12．
故选：D．
【名师指导】
平面向量线性运算问题的常见类型及解题策略
(1)向量加法或减法的几何意义：向量加法和减法均适合三角形法则．
(2)求已知向量的和：一般共起点的向量求和用平行四边形法则；求差用三角形法则；求首尾相连向量的和用三角形法则．
题型3 共线向量定理的应用
【例3-1】（2020春•新余期末）已知两个非零向量e1→，e2→不共线，若AB→=λe1→+3e2→，BC→=6e1→+23e2→，CD→=4e1→-8e2→，且A、B、D三点共线，则λ等于 ．
【分析】可求出BD→=10e1→+15e2→，根据A，B，D三点共线即可得出λe1→+3e2→=10ke1→+15ke2→，然后根据平面向量基本定理即可求出λ的值．
【解答】解：BD→=BC→+CD→=10e1→+15e2→，
∵A，B，D三点共线，
∴设AB→=kBD→，即λe1→+3e2→=10ke1→+15ke2→，
∴λ=10k15k=3，解得λ＝2．
故答案为：2．
【例3-2】（2019春•西城区校级期中）向量OA→=（k，12），OB→=（4，5），OC→=（10，k），当k为何值时，A、B、C三点共线．
【分析】由条件和向量的坐标运算求出AB→、BC→的坐标，再代入向量共线的坐标条件求出k的值．
【解答】解：由题意得，AB→=（4﹣k，﹣7），BC→=（6，k﹣5），
∵A、B、C三点共线，∴AB→∥BC→，
∴（4﹣k）（k﹣5）+42＝0，即k2﹣9k﹣22＝0，
解得k＝﹣2或k＝11．
综上知，当k＝﹣2或k＝11时，A、B、C三点共线
【跟踪训练3-1】（2020•江都区校级模拟）在△ABC中，点D，E分别在边AB，BC上，且AD＝DB，BE＝2EC，记AB→=a→，AC→=b→，若DE→=xa→+yb→，则x+y的值为 ．
【分析】可画出图形，根据AD＝DB，BE＝2EC即可得出DB→=12AB→，BE→=23(AC→-AB→)，再根据AB→=a→，AC→=b→便可得出DE→=-16a→+23b→，又知DE→=xa→+yb→，这样根据平面向量基本定理即可求出x，y的值．
【解答】解：如图，
∵AD＝DB，BE＝2EC；
∴DB→=12AB→，BE→=23BC→=23(AC→-AB→)，且AB→=a→，AC→=b→；
∴DE→=DB→+BE→=12a→+23(b→-a→)=-16a→+23b→；
又DE→=xa→+yb→；
∴根据平面向量基本定理得，x=-16，y=23；
∴x+y=12．
故答案为：12．
【跟踪训练3-2】（2020•茂名二模）设a→，b→是不共线的两个平面向量，已知AB→=a→-2b→，BC→=3a→+kb→(k∈R)，若A，B，C三点共线，则k＝（ ）
A．2B．﹣2C．6D．﹣6
【分析】根据题意，分析可得AB→∥BC→，进而可得k-2=31，解可得k的值，即可得答案．
【解答】解：根据题意，若A，B，C三点共线，则AB→∥BC→，
又由AB→=a→-2b→，BC→=3a→+kb→(k∈R)，则有k-2=31，
解可得k＝﹣6；
故选：D．
【跟踪训练3-3】（2020春•临川区校级期中）设a→，b→不共线，AB→=a→+3b→，BC→=a→+2b→，CD→=3a→+mb→，若A，C，D三点共线，则实数m的值是（ ）
A．23B．15C．72D．152
【分析】根据A，C，D三点共线，得到AC→=λCD→，即可求解结论．
【解答】解：∵AB→=a→+3b→，BC→=a→+2b→，∴AC→=AB→+BC→=2a→+5b→，
∵A，C，D三点共线，∴AC→=λCD→，即2a+5b＝λ（3a+mb），
∴2=3λ5=λm，解得λ=23m=152．
故选：D．
【名师指导】
利用向量共线定理证明三点共线
若存在实数λ，使eq \(AB,\s\up7(―→))＝λeq \(AC,\s\up7(―→))，则A，B，C三点共线．
[提醒] (1)使用向量共线基本定理的大前提是至少有一个向量是非零向量．
(2)证明三点共线时，需说明共线的两向量有公共点．名称
定义
备注
零向量
长度为0的向量
零向量记作0，其方向是任意的
单位
向量
长度等于1个单位的向量
单位向量记作a0，a0＝eq \f(a,|a|)
平行
向量
方向相同或相反的非零向量(也叫共线向量)
0与任意向量共线
相等
向量
长度相等且方向相同的向量
相等向量一定是平行向量，平行向量不一定是相等向量
相反
向量
长度相等且方向相反的两个向量
若a，b为相反向量，则a＝－b
向量运算
定义
法则(或几何意义)
运算律
加法
求两个向量和的运算

三角形法则 eq \a\vs4\al(平行四边形,法则)
(1)交换律：
a＋b＝b＋a；
(2)结合律：
(a＋b)＋c＝
a＋(b＋c)
减法
求a与b的相反向量－b的和的运算叫做a与b的差
三角形法则
a－b＝a＋(－b)
数乘
求实数λ与向量a的积的运算
|λa|＝|λ||a|；当λ＞0时，λa的方向与a的方向相同；当λ＜0时，λa的方向与a的方向相反；当λ＝0时，λa＝0
λ(μa)＝(λμ)a；
(λ＋μ)a＝λa＋μa；
λ(a＋b)＝λa＋λb