




高中数学人教A版 (2019)必修 第二册10.3 频率与概率备课ppt课件
展开10.3.1 频率的稳定性
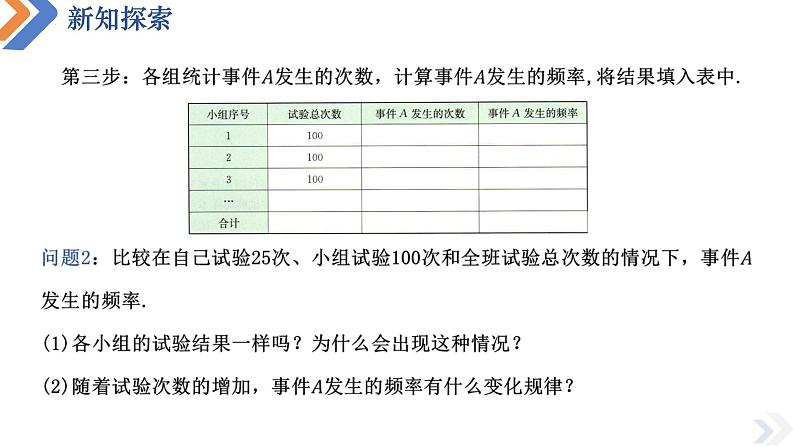
对于样本点等可能的实验,我们可以用古典概型公式计算有关事件的概率.但在现实中,很多试验的样本点往往是等可能的或者是否等可能不容易判断.例如,抛掷一枚质地不均匀的骰子,或者投掷一枚图钉,此时无法通过古典概型公式计算有关事件的概率,我们需要寻求新的求概率的方法.
我们知道,事件的概率越大,意味着事件发生的可能性越大,在重复试验中,相应的频率一般也越大;事件的概率越小,则事件发生的可能性越小,在重复试验中,相应的频率一般也越小.在初中,我们利用频率与概率的这种关系,通过大量重复试验,用频率去估计概率.那么,在重复试验中,频率的大小是否就决定了概率的大小呢?频率与概率之间到底是一种怎样的关系呢?
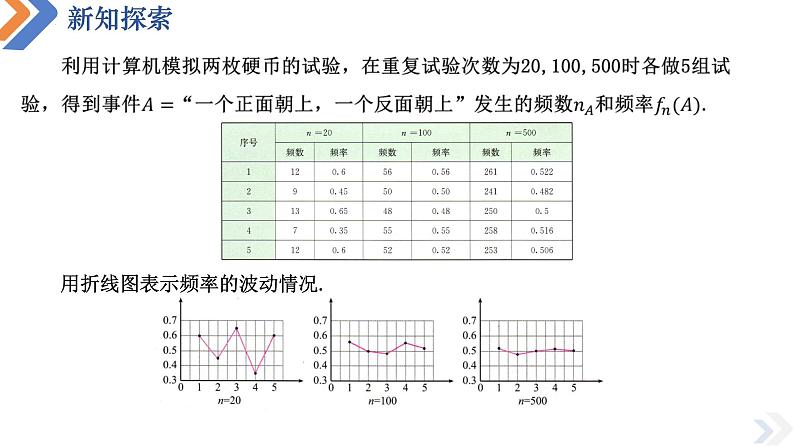
用折线图表示频率的波动情况.
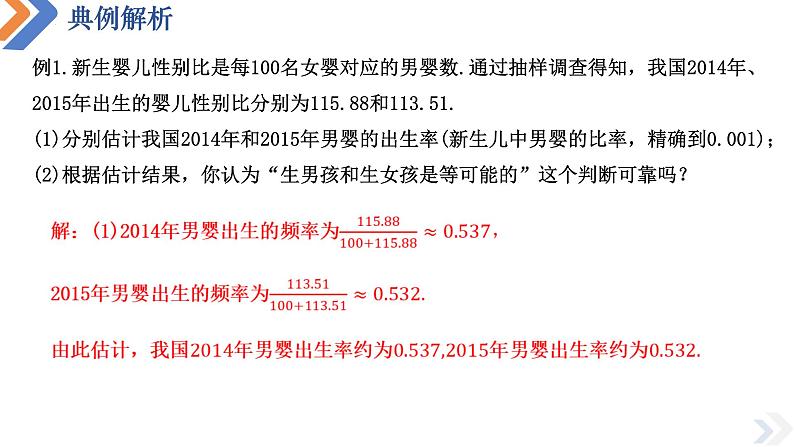
例1.新生婴儿性别比是每100名女婴对应的男婴数.通过抽样调查得知,我国2014年、2015年出生的婴儿性别比分别为115.88和113.51.(1)分别估计我国2014年和2015年男婴的出生率(新生儿中男婴的比率,精确到0.001);(2)根据估计结果,你认为“生男孩和生女孩是等可能的”这个判断可靠吗?
解:(2)由于调查新生儿人数的样本非常大,根据频率的稳定性,上述对男婴出生率的估计有较高的可信度.因此,我们有理由怀疑“生男孩和生女孩是等可能的”的结论.
解:当游戏玩了10次时,甲、乙获胜的频率都是0.5;当游戏玩了1000次时,甲获胜的频率为0.3,乙获胜的频率为0.7.根据频率的稳定性,随着试验次数的增加,频率偏离概率很大的可能性会越来越小.相对10次游戏,1000次游戏时的频率接近概率的可能性更大,因此我们更愿意相信1000次时的频率离概率更近.而游戏玩到1000次时,甲、乙获胜的频率分别是0.3和0.7,存在很大差距,所以有理由认为游戏是不公平的.因此,应该支持甲对游戏公平性的判断.
问题3:气象工作者有时用概率预报天气,如某气象台预报“明天的降水概率是90%.如果您明天要出门,最好携带雨具”.如果第二天没有下雨,我们或许会抱怨气象台预报得不准确.那么如何理解“降水概率是90%”?又该如何评价预报的结果是否准确呢?
降水的概率是气象专家根据气象条件和经验,经分析推断得到的.对“降水的概率为90%”比较合理的解释是:大量观察发现,在类似的气象条件下,大约有90%的天数要下雨. 只有根据气象预报的长期记录,才能评价预报的准确性.如果在类似气象条件下预报要下雨的那些天(天数较多)里,大约有90%确实要下雨了,那么应该认为预报是准确的;如果真实下雨的天数所占的比例与90%差别较大,那么就可以认为预报不太准确.
10.3.2 随机模拟
画出频率折线图,从图中可以看出:随着试验次数的增加,摸到红球的频率稳定于概率0.4.
我们称利用随机模拟解决问题的方法为蒙特卡洛方法.
解:方法1 根据假设,每个人的出生月份在12个月中是等可能的,而且相互之间没有影响,所以观察6个人的出生月份可以看成可重复试验. 因此,可以构建如下有放回摸球试验进行模拟:在袋子中装入编号为1,2,…,12的12个球,这些球除编号外没有什么差别.有放回地随机从袋中摸6次球,得到6个数代表6个人的出生月份,这就完成了一次模拟试验.如果这6个数中至少有2个相同,表示事件发生了.重复以上模拟试验20次,就可以统计出事件发生的频率.
例4.在一次奥运会男子羽毛球单打比赛中,运动员甲和乙进入了决赛.假设每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4.利用计算机模拟试验,估计甲获得冠军的概率.
答案:D.解:①错,次品率是大量产品的估计值,并不是针对200件产品来说的.②③混淆了频率与概率的区别.④正确.
例2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:(1)若每辆车的投保金额为2800元,估计赔付金额大于投保金额的概率;
例2.某保险公司利用简单随机抽样的方法,对投保的车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
变2.某公司在过去几年内使用了某种型号的灯管1000支,该公司对这些灯管的使用寿命(单位:时)进行了统计,统计结果如下表所示:(1)将各组的频率填入表中;(2)根据上述统计结果,估计灯管使用寿命不足1500小时的概率.
例3.有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子中摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
例3.有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.(2)摸球方法与(1)相同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由.
方法技巧: 游戏公平性的标准及判断方法 (1)标准:游戏规则是否公平,要看对游戏的双方来说,获胜的可能性或概率是否相同.若相同,则规则公平,否则就是不公平.(2)判断方法:具体判断时,可以求出按所给规则双方的获胜概率,再进行比较.
变3.转盘被平均分成10等份(如图所示),转动转盘,当转盘停止后,指针指向的数字即为转出的数字.游戏规则如下:两个人参加,先确定猜数方案,甲转动转盘,乙猜,若猜出的结果与转盘转出的数字所表示的特征相符,则乙获胜,否则甲获胜.猜数方案从以下两种方案中选一种:A.猜“是奇数”或“是偶数”;B.猜“是4的整数倍”或“不是4的整数倍”.请回答下列问题:(1)为了尽可能获胜,乙应怎么选?(2)为了保证游戏的公平性,乙应选哪种猜数方案?
人教A版 (2019)必修 第二册10.3 频率与概率教学ppt课件: 这是一份人教A版 (2019)必修 第二册<a href="/sx/tb_c4000316_t3/?tag_id=26" target="_blank">10.3 频率与概率教学ppt课件</a>,共60页。PPT课件主要包含了知识梳理,题型探究,随堂演练,课时对点练等内容,欢迎下载使用。
人教A版 (2019)必修 第二册10.3 频率与概率教课内容课件ppt: 这是一份人教A版 (2019)必修 第二册10.3 频率与概率教课内容课件ppt,共28页。PPT课件主要包含了导入新课,精彩课堂,典型例题,课堂练习,课堂总结等内容,欢迎下载使用。
数学必修 第二册10.3 频率与概率教学ppt课件: 这是一份数学必修 第二册10.3 频率与概率教学ppt课件,文件包含专题一近代中国人民的反侵略斗争同步练习教师版2023-2024部编版历史八年级上册docx、专题一近代中国人民的反侵略斗争同步练习学生版2023-2024部编版历史八年级上册docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。













