山西省运城市盐湖区2022-2023学年九年级上学期期中数学试卷

这是一份山西省运城市盐湖区2022-2023学年九年级上学期期中数学试卷，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）若x＝1是方程x2+mx﹣n＝0的一个根，则m﹣n的值为（ ）
A．1B．0C．﹣1D．无法确定
2．（3分）下列说法正确的是（ ）
A．某彩票的中奖概率是1%，那么买100张彩票一定有1张中奖
B．某次试验投掷图钉500次，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616
C．如果一个事件发生的可能性很小，那么它的概率为0
D．试验得到的频率与概率不可能相等
3．（3分）用配方法解方程x2+6x﹣7＝0时，原方程应变形为（ ）
A．（x+3）2＝2B．（x+3）2＝16C．（x+6）2＝2D．（x+6）2＝16
4．（3分）如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A（﹣9，0），（6，0），点D在y轴上，则点C的坐标是（ ）
A．（9，6）B．（﹣15，12）C．（﹣9，6）D．（15，12）
5．（3分）下面一定相似的一组图形为（ ）
A．两个等腰三角形B．两个矩形
C．两个等边三角形D．两个菱形
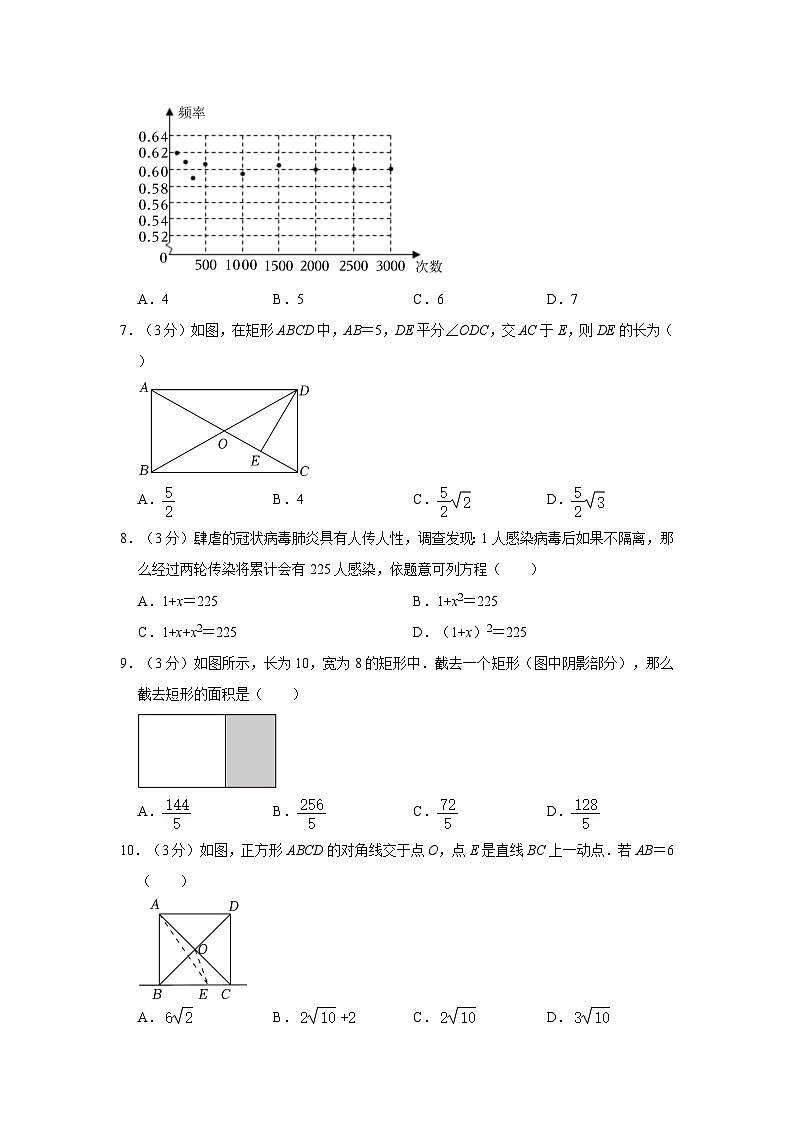
6．（3分）在一个不透明的口袋中，放置4个黄球和n个蓝球，这些小球除颜色外其余均相同，并且统计了蓝球出现的频率（如图所示），则n的值最可能是（ ）
A．4B．5C．6D．7
7．（3分）如图，在矩形ABCD中，AB＝5，DE平分∠ODC，交AC于E，则DE的长为（ ）
A．B．4C．D．
8．（3分）肆虐的冠状病毒肺炎具有人传人性，调查发现：1人感染病毒后如果不隔离，那么经过两轮传染将累计会有225人感染，依题意可列方程（ ）
A．1+x＝225B．1+x2＝225
C．1+x+x2＝225D．（1+x）2＝225
9．（3分）如图所示，长为10，宽为8的矩形中．截去一个矩形（图中阴影部分），那么截去短形的面积是（ ）
A．B．C．D．
10．（3分）如图，正方形ABCD的对角线交于点O，点E是直线BC上一动点．若AB＝6（ ）
A．B．C．D．
二、填空题（每题3分，共15分）
11．（3分）如图，已知四边形ABCD是平行四边形，请补充一个条件 ．（写一个即可）
12．（3分）若x：y＝2：3，则＝ ．
13．（3分）圆周率π是无限不循环小数．历史上，祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究．目前，超级计算机已计算出π的小数部分超过31.4万亿位．有学者发现，0～9这10个数字出现的频率趋于稳定接近相同，从π的小数部分随机取出一个数字 ．
14．（3分）已知关于x的方程x2﹣（k+2）x+2k＝0，若等腰三角形ABC的一边长a＝3，c恰好是这个方程的两个根，则△ABC的周长为 ．
15．（3分）如图，在矩形ABCD中，E是BC上一动点，点F在矩形ABCD内部，延长AF交CD于点G，AD＝8．当点E是BC的中点时，线段GC的长为 ；点E在运动过程中，当△CFE的周长最小时，CE的长为 ．
三、解答题（解答应写出文字说明、证明过程或演算步骤。本大题共8个小题，共75分）
16．（8分）用适当的方法解方程：
（1）x2﹣x﹣1＝0；
（2）3x（x﹣1）＝2（1﹣x）．
17．（8分）如图，在4×4的正方形网格图中，点A、B均在格点上
（注：作图仅能使用无刻度的直尺，且要求保留作图痕迹．请你借助网格图完成第（2）、（3）、（4）小题的作图）．
（1）直接写出线段AB的长为 ；
（2）在网格图中找一个格点C，连接BC，使BC⊥AB；
（3）在网格图中，用正确的方法画出线段AB的中点D；
（4）连接AC并在线段AC上找一点E，连接DE，使DE∥BC．
18．（8分）2022年冬季奥运会和冬季残奥会两件赛事在我国首都北京和河北省石家庄市举行，某商家购进了冬季残奥会吉祥物“雪容融”纪念品，每个的进价是30元．为了增大“雪容融”类纪念品的销售量，当销售价为每个44元时，每天可以售出20个，每天将多售出5个．请问商家应将“雪容融”类纪念品每个降价多少元时，每天售出此类纪念品能获利400元？
19．（10分）如图，在△ABC中，∠C＝90°，∠ABC的角平分线交于点G，GE⊥BC于点E
（1）求证：四边形GECF是正方形；
（2）若AC＝4，BC＝3，求四边形GECF的周长．
20．（10分）2022年4月15日是第七个全民国家安全教育日．为增强师生的国家安全意识，我区某中学组织了“国家安全知识竞赛”，根据学生的成绩划分为A、B、C、D四个等级
根据图中提供的信息，回答下列问题：
（1）参加知识竞赛的学生共有 人；
（2）扇形统计图中，m＝ ，C等级对应的圆心角为 度；
（3）小永是四名获A等级的学生中的一位，学校将从获A等级的学生中任选2人，参加区举办的知识竞赛，求小永被选中参加区知识竞赛的概率．
21．（8分）读材料：各类方程的解法
求解一元一次方程，根据等式的基本性质，把方程转化为x＝a的形式．求解二元一次方程组，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解．各类方程的解法不尽相同，把未知转化为已知．用“转化”的数学思想，我们还可以解一些新的方程．例如3+x2﹣2x＝0，可以通过因式分解把它转化为x（x2+x﹣2）＝0，解方程x＝0和x2+x﹣2＝0，可得方程x3+x2﹣2x＝0的解．
（1）问题：方程x3+x2﹣2x＝0的解是x1＝0，x2＝ ，x3＝ ；
（2）拓展：用“转化”思想求方程的解．
22．（12分）如图，在Rt△ABC中，∠B＝90°，∠C＝30°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒．过点D作DF⊥BC于点F，EF．
（1）四边形AEFD能构成菱形吗？如果能，求出相应的t值；如果不能；
（2）当t为何值时，△DEF为直角三角形？请说明理由．
23．（11分）如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形ABCD中，AB＝AD，问四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论：（要求用文字语言叙述）
写出证明过程（先画出图形，写出已知、求证）．
（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，GE，已知AC＝4，求GE长．
2022-2023学年山西省运城市盐湖区九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（每小题3分，共30分）
1．（3分）若x＝1是方程x2+mx﹣n＝0的一个根，则m﹣n的值为（ ）
A．1B．0C．﹣1D．无法确定
【分析】根据一元二次方程的解的定义，将x＝1代入一元二次方程x2+mx﹣n＝0，即可求得m+n的值．
【解答】解：∵x＝1是一元二次方程x2+mx﹣n＝6的一个根，
∴x＝1满足一元二次方程x2+mx﹣n＝7，
∴12+m﹣n＝8，
∴m﹣n＝﹣1；
故选：C．
【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根．
2．（3分）下列说法正确的是（ ）
A．某彩票的中奖概率是1%，那么买100张彩票一定有1张中奖
B．某次试验投掷图钉500次，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616
C．如果一个事件发生的可能性很小，那么它的概率为0
D．试验得到的频率与概率不可能相等
【分析】利用概率的意义和概率公式分别对每一项进行分析，即可得出答案．
【解答】A、某彩票的中奖概率是1%，故A不符合题意；
B、某次试验投掷500次，则该次试验“钉尖向上”的频率是0.616；
C、如果一个事件发生的可能性很小，故C不符合题意；
D、试验得到的频率与概率可能相等；
故选：B．
【点评】此题主要考查了概率的意义和概率公式，解决的关键是理解概率的意义和概率公式．
3．（3分）用配方法解方程x2+6x﹣7＝0时，原方程应变形为（ ）
A．（x+3）2＝2B．（x+3）2＝16C．（x+6）2＝2D．（x+6）2＝16
【分析】先把常数项移到方程右边，再把方程两边加上9，然后把方程左边写成完全平方的形式即可．
【解答】解：x2+6x﹣5＝0，
x2+7x＝7，
x2+5x+9＝16，
（x+3）5＝16．
故选：B．
【点评】本题考查了解一元二次方程﹣配方法：熟练掌握用配方法解一元二次方程的一般步骤是解决问题的关键．
4．（3分）如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A（﹣9，0），（6，0），点D在y轴上，则点C的坐标是（ ）
A．（9，6）B．（﹣15，12）C．（﹣9，6）D．（15，12）
【分析】由菱形的性质得AD＝AB＝DC＝15，CD∥AB，再由勾股定理求出OD＝12，即可得出结论．
【解答】解：∵A（﹣9，0），6），
∴OA＝9，OB＝6，
∴AB＝OA+OB＝15，
∵四边形ABCD是菱形，
∴AD＝AB＝DC＝15，CD∥AB，
在Rt△ADO中，OD＝＝，
∴C（15，12），
故选：D．
【点评】本题考查菱形的性质、坐标与图形性质以及勾股定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
5．（3分）下面一定相似的一组图形为（ ）
A．两个等腰三角形B．两个矩形
C．两个等边三角形D．两个菱形
【分析】根据相似图形的定义判断即可．
【解答】解：两个等腰三角形，两个矩形，两个等边三角形一定相似．
故选：C．
【点评】本题考查相似图形，等边三角形的性质，矩形的性质，菱形的性质等知识，解题的关键是掌握相似图形的定义，属于中考常考题型．
6．（3分）在一个不透明的口袋中，放置4个黄球和n个蓝球，这些小球除颜色外其余均相同，并且统计了蓝球出现的频率（如图所示），则n的值最可能是（ ）
A．4B．5C．6D．7
【分析】利用频率估计概率，由概率列方程求解即可．
【解答】解：由频率分布图可知，当实验的次数逐渐增大时，
因此摸到蓝球的概率为0.6，
所以＝0.6，
解得n＝3，
经检验，n＝6是原方程的解，
因此n最可能有6．
故选：C．
【点评】本题考查频率估计概率，理解频率、概率的意义和相互关系是正确解答的关键．
7．（3分）如图，在矩形ABCD中，AB＝5，DE平分∠ODC，交AC于E，则DE的长为（ ）
A．B．4C．D．
【分析】由矩形的性质得出OA＝OD＝OC，得出∠OAD＝∠ODA，由已知条件得出OE＝CE，∠DEA＝90°，由线段垂直平分线的性质得出OD＝CD，得出△OCD为等边三角形，因此∠DOC＝60°，由三角形的外角性质得出∠DAC＝30°，由含30°角的直角三角形的性质即可得出DE的长．
【解答】解：∵四边形ABCD是矩形，
∴OA＝ACBD，
∴OA＝OD＝OC，
∴∠OAD＝∠ODA，
∵AE＝3CE，
∴OE＝CE，
∵DE平分∠ODC，
∴DE⊥OC，
∴∠DEA＝90°，
∴OD＝CD，
∴OC＝OD＝CD，
∴△OCD为等边三角形，
∴∠DOC＝60°，
∴∠DAC＝30°，
∵CD＝AB＝5，
∴AC＝2CD＝10，
∴AD＝CD＝8，
∴DE＝AD＝．
故选：C．
【点评】本题考查了矩形的性质，等边三角形的判定和性质，直角三角形的性质，线段垂直平分线的性质，证明△ABO是等边三角形是本题的关键．
8．（3分）肆虐的冠状病毒肺炎具有人传人性，调查发现：1人感染病毒后如果不隔离，那么经过两轮传染将累计会有225人感染，依题意可列方程（ ）
A．1+x＝225B．1+x2＝225
C．1+x+x2＝225D．（1+x）2＝225
【分析】本题可设1人平均感染x人，则第一轮共感染（x+1）人，第二轮共感染x（x+1）+x+1＝（x+1）（x+1）人，根据题意列方程即可．
【解答】解：设1人平均感染x人，
依题意可列方程：1+x+（5+x）x＝225，（x+1）2＝225．
故选：D．
【点评】本题考查了由实际问题抽象出一元二次方程，找到关键描述语，找到等量关系准确地列出方程是解决问题的关键．
9．（3分）如图所示，长为10，宽为8的矩形中．截去一个矩形（图中阴影部分），那么截去短形的面积是（ ）
A．B．C．D．
【分析】根据题意，剩下矩形与原矩形相似，利用相似形的对应边的比相等可得．
【解答】解：如图，在矩形ABDC中截取矩形ABFE，
则矩形ABDC∽矩形FDCE，
则＝，
设DF＝xcm，得到：＝，
解得：x＝2.4，
则剩下的矩形面积是：6.4×8＝（cm7）．
故选：B．
【点评】本题考查了相似形的对应边的比相等，分清矩形的对应边是解决本题的关键．
10．（3分）如图，正方形ABCD的对角线交于点O，点E是直线BC上一动点．若AB＝6（ ）
A．B．C．D．
【分析】作点A关于直线BC的对称点A'，再连接A'O，运用两点之间线段最短得到A'O为所求最小值，再运用勾股定理求线段A'O的长度即可．
【解答】解：如图所示，作点A关于直线BC的对称点A'，其与BC的交点即为点E，
∵A与A'关于BC对称，
∴AE＝A'E，AE+OE＝A'E+OE，O，E在同一条线上的时候和最小，此时：AE+OE＝A'E+OE＝A'O，
∵正方形ABCD，点O为对角线的交点，
∴OF＝3，
∵A与A'关于BC对称，
∴AB＝BA'＝6，
∴FA'＝FB+BA'＝3+6＝9，
在Rt△OFA'中，
OA′＝＝3，
故选：D．
【点评】本题考查了轴对称﹣最短路径问题，熟练掌握轴对称的性质及勾股定理是解题的关键．
二、填空题（每题3分，共15分）
11．（3分）如图，已知四边形ABCD是平行四边形，请补充一个条件 ∠BAD＝90° ．（写一个即可）
【分析】添加条件是∠BAD＝90°，根据矩形的判定推出即可．
【解答】解：添加条件∠BAD＝90°，
理由是：∵四边形ABCD是平行四边形，∠BAD＝90°，
∴四边形ABCD是矩形，
故答案为：∠BAD＝90°．
【点评】本题考查了矩形的判定的应用，掌握矩形的判定方法是解决此题的关键．
12．（3分）若x：y＝2：3，则＝ ．
【分析】根据已知条件得出y＝x，再代入要求的式子进行计算，即可得出答案．
【解答】解：∵x：y＝2：3，
∴y＝x，
∴＝．
故答案为：．
【点评】此题考查了比例的性质，掌握比例的基本性质是解题的关键，较简单．
13．（3分）圆周率π是无限不循环小数．历史上，祖冲之、刘徽、韦达、欧拉等数学家都对π有过深入的研究．目前，超级计算机已计算出π的小数部分超过31.4万亿位．有学者发现，0～9这10个数字出现的频率趋于稳定接近相同，从π的小数部分随机取出一个数字 ．
【分析】从π的小数部分随机取出一个数字共有10种等可能的结果，其中出现数字6的只有1种结果，利用概率公式求解即可．
【解答】解：∵随着π小数部分位数的增加，0～9这10个数字出现的频率趋于稳定接近相同，
∴从π的小数部分随机取出一个数字共有10种等可能的结果，其中出现数字2的只有1种结果，
∴P（数字是6）＝．
故答案为：．
【点评】本题考查了利用频率估计概率，掌握大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率是解题的关键．
14．（3分）已知关于x的方程x2﹣（k+2）x+2k＝0，若等腰三角形ABC的一边长a＝3，c恰好是这个方程的两个根，则△ABC的周长为 8或7 ．
【分析】分两种情况考虑：当b＝c时，求出方程的解，进而得到三角形周长；当a＝c或a＝b时，把x＝3代入方程求出k的值，进而求出周长即可．
【解答】解：∵Δ＝（k+2）2﹣2k
＝k2+4k+7﹣8k
＝k2﹣3k+4
＝（k﹣2）2≥0，
则无论k取何实数值，方程总有实数根，
当b＝c时，k＝23﹣4x+4＝8，
解得：x1＝x2＝5，
此时三边长为3，2，4，周长为3+2+8＝7；
当a＝b＝3或a＝c＝5时，把x＝3代入方程得：9﹣6（k+2）+2k＝8，
解得：k＝3，此时方程为：x2﹣7x+6＝0，
解得：x8＝2，x2＝8，
此时三边长为3，3，5，周长为3+3+8＝8，
综上所述，△ABC的周长为7或3．
故答案为：8或7．
【点评】此题考查了根与系数的关系，根的判别式，三角形三边关系，以及等腰三角形的性质，熟练掌握各自的性质是解本题的关键．
15．（3分）如图，在矩形ABCD中，E是BC上一动点，点F在矩形ABCD内部，延长AF交CD于点G，AD＝8．当点E是BC的中点时，线段GC的长为 ；点E在运动过程中，当△CFE的周长最小时，CE的长为 5 ．
【分析】连接GE，根据点E是BC的中点以及翻折的性质可以求出BE＝EF＝EC，然后利用“HL”证明△GFE和△GCE全等，根据全等三角形对应边相等即可得证FG＝CG，设GC＝x，表示出AG、DG，然后在Rt△ADG中，利用勾股定理列式进行计算即可得解；先判断出EF⊥AC时，△CEF的周长最小，最后用勾股定理即可得出结论．
【解答】解：如图，连接GE，
∵E是BC的中点，
∴BE＝EC，
∵△ABE沿AE折叠后得到△AFE，
∴BE＝EF，∠EFA＝∠B，BC＝AD＝8
∴EF＝EC，
在矩形ABCD中，
∴∠B＝∠C＝90°，DC＝AB＝6，
∴∠EFG＝90°，
在Rt△GFE和Rt△GCE中，
，
∴Rt△GFE≌Rt△GCE（HL），
∴GF＝GC，
设GC＝x，则AG＝4+x，
在Rt△ADG中，AD2+DG2＝AG8
∴82+（4﹣x）2＝（6+x）2，
解得x＝．
如图7，由折叠知，EF＝BE，
∴EF+CE＝BE+CE＝BC＝AD＝8，
∴当CF最小时，△CEF的周长最小，
而当CF⊥EF时，CF最小，
即：∠CFE＝90°，
∵∠AFE＝90°，
∴∠AFE+∠CFE＝180°，
∴点A，F，C在同一条直线上时，
由折叠知，AF＝AB＝6，
在Rt△ABC中，AB＝8，
∴AC＝＝10，
∴CF＝AC﹣AF＝5，
在Rt△CEF中，EF2+CF2＝CE2，
∴BE2+CF2＝（3﹣BE）2，
∴BE2+22＝（8﹣BE）5，
∴BE＝3．
∴CE＝BC﹣BE＝5；
故答案为：，5．
【点评】此题是四边形综合题，主要考查了矩形的性质，折叠的性质，全等三角形的判定和性质，勾股定理，解（1）的关键是利用勾股定理求解，解（2）的关键是构造出直角三角形，利用勾股定理解决问题．
三、解答题（解答应写出文字说明、证明过程或演算步骤。本大题共8个小题，共75分）
16．（8分）用适当的方法解方程：
（1）x2﹣x﹣1＝0；
（2）3x（x﹣1）＝2（1﹣x）．
【分析】（1）利用因式分解法解方程即可；
（2）移项，然后把方程左边分解因式，利用因式分解法即可求解．
【解答】解：（1）x2﹣x﹣1＝6，
a＝1，b＝c＝﹣1，
∴Δ＝5+4＝5＞4，
∴x＝，
解得x1＝，x2＝；
（2）4x（x﹣1）＝2（5﹣x），
移项，得：3x（x﹣1）﹣3（1﹣x）＝0，
分解因式，得：（x﹣5）（3x+2）＝8，
则x﹣1＝0或3x+2＝0，
解得x3＝1，x2＝﹣．
【点评】本题考查了一元二次方程的解法．解一元二次方程常用的方法有直接开平方法，配方法，公式法，因式分解法，要根据方程的特点灵活选用合适的方法．
17．（8分）如图，在4×4的正方形网格图中，点A、B均在格点上
（注：作图仅能使用无刻度的直尺，且要求保留作图痕迹．请你借助网格图完成第（2）、（3）、（4）小题的作图）．
（1）直接写出线段AB的长为 ；
（2）在网格图中找一个格点C，连接BC，使BC⊥AB；
（3）在网格图中，用正确的方法画出线段AB的中点D；
（4）连接AC并在线段AC上找一点E，连接DE，使DE∥BC．
【分析】（1）利用勾股定理求解即可．
（2）取格点C，连接BC即可．
（3）取格点P，Q，连接PQ交AB于点D，点D即为所求作．
（4）錒AC的中点E，连接DE即可．
【解答】解：（1）直接写出线段AB的长＝＝．
故答案为：．
（2）如图，线段BC即为所求作．
（3）如图，点D即为所求作．
（4）如图，线段DE即为所求作．
【点评】本题考查作图﹣应用与设计作图，三角形的中位线等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考常考题型．
18．（8分）2022年冬季奥运会和冬季残奥会两件赛事在我国首都北京和河北省石家庄市举行，某商家购进了冬季残奥会吉祥物“雪容融”纪念品，每个的进价是30元．为了增大“雪容融”类纪念品的销售量，当销售价为每个44元时，每天可以售出20个，每天将多售出5个．请问商家应将“雪容融”类纪念品每个降价多少元时，每天售出此类纪念品能获利400元？
【分析】设商家应将“雪容融”类纪念品每个降价x元，则“雪容融”类纪念品每个的销售利润为（44﹣x﹣30）元，每天可以售出（20+5x）元，利用总利润＝每个的销售利润×日销售量，即可得出关于x的一元二次方程，解之即可得出结论．
【解答】解：设商家应将“雪容融”类纪念品每个降价x元，则“雪容融”类纪念品每个的销售利润为（44﹣x﹣30）元，
依题意得：（44﹣x﹣30）（20+5x）＝400，
整理得：x2﹣10x+24＝7，
解得：x1＝4，x8＝6．
答：当商家将“雪容融”类纪念品每个降价4元或6元时，每天售出此类纪念品能获利400元．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
19．（10分）如图，在△ABC中，∠C＝90°，∠ABC的角平分线交于点G，GE⊥BC于点E
（1）求证：四边形GECF是正方形；
（2）若AC＝4，BC＝3，求四边形GECF的周长．
【分析】（1）过G作GD⊥AB于G，由角平分线的性质可求出GF＝GE，由正方形的判定定理即可证明；
（2）设EG＝x，则DG＝FG＝x，利用面积法列等式可得x的值，因为四边形GECF是正方形，所以四边形GECF的周长＝4EG，从而得结论．
【解答】（1）证明：过G作GD⊥AB于D，
∵∠CAB、∠CBA的角平分线交于G点，GF⊥AC于点F，
∴DG＝EG，DG＝FG，
∴EG＝FG，
∵△ABC是直角三角形，∠C＝90°，GF⊥AC，
∴∠C＝∠CEG＝∠CFG＝90°，
∴四边形GECF是矩形，
∵EG＝FG，
∴四边形GECF为正方形；
（2）解：如图2，连接CG，
由勾股定理得：AB＝＝5，
设EG＝x，则DG＝FG＝x，
∵S△ABC＝S△AGB+S△AGC+S△BCG，
∴×3×4＝•6x+，
∴x＝2，
∴四边形GECF的周长＝4EG＝4．
【点评】本题考查了正方形的判定与性质，角平分线的性质，准确作出辅助线，得出EG＝FG是解决第（1）问的关键；利用面积法列等式是解决第（2）问的关键．
20．（10分）2022年4月15日是第七个全民国家安全教育日．为增强师生的国家安全意识，我区某中学组织了“国家安全知识竞赛”，根据学生的成绩划分为A、B、C、D四个等级
根据图中提供的信息，回答下列问题：
（1）参加知识竞赛的学生共有 40 人；
（2）扇形统计图中，m＝ 10 ，C等级对应的圆心角为 144 度；
（3）小永是四名获A等级的学生中的一位，学校将从获A等级的学生中任选2人，参加区举办的知识竞赛，求小永被选中参加区知识竞赛的概率．
【分析】（1）根据D等级的人数和所占的百分比即可得出答案；
（2）用A等级的人数除以总人数，求出m的值，再用360°乘以C等级所占的百分比即可；
（3）根据题意画出树状图得出所有等可能的情况数，找出小永被选中参加区知识竞赛的情况数，然后根据概率公式即可得出答案．
【解答】解：（1）参加知识竞赛的学生共有：12÷30%＝40（人）；
故答案为：40；
（2）m%＝×100%＝10%；
C等级对应的圆心角为：360°×（1﹣20%﹣10%﹣30%）＝144°；
故答案为：10，144；
（3）小永用A表示，其他5名同学分别用B、C，
根据题意画图如下：
共有12种等可能的情况数，其中小永被选中参加区知识竞赛的有6种，
则小永被选中参加区知识竞赛的概率是＝．
【点评】本题考查条形统计图、扇形统计图的意义和制作方法、列表法树状图法求随机事件发生的概率，从统计图中获取数量和数量之间的关系以及列举出所有可能出现的结果数是解决问题的关键．
21．（8分）读材料：各类方程的解法
求解一元一次方程，根据等式的基本性质，把方程转化为x＝a的形式．求解二元一次方程组，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解．各类方程的解法不尽相同，把未知转化为已知．用“转化”的数学思想，我们还可以解一些新的方程．例如3+x2﹣2x＝0，可以通过因式分解把它转化为x（x2+x﹣2）＝0，解方程x＝0和x2+x﹣2＝0，可得方程x3+x2﹣2x＝0的解．
（1）问题：方程x3+x2﹣2x＝0的解是x1＝0，x2＝ ﹣2 ，x3＝ 1 ；
（2）拓展：用“转化”思想求方程的解．
【分析】（1）通过因式分解把方程转化为x（x2+x﹣2）＝0，再用因式分解法求解x2+x﹣2＝0即可；
（2）方程两边平方，把无理方程先转化为整式方程，求解整式方程并检验．
【解答】解：（1）x3+x2﹣6x＝0，
x（x2+x﹣5）＝0，
∴x（x+2）（x﹣7）＝0．
∴x＝0或x+8＝0或x﹣1＝6．
∴x1＝0，x3＝﹣2，x3＝6．
故答案为：﹣2，1．
（2）方程的两边平方，得5x+5＝x2，
即x5﹣4x﹣5＝5，
（x﹣5）（x﹣1）＝8，
∴x1＝5，x8＝﹣1，
经检验：当x＝5时，左边＝，x＝5是原方程的解，
当x＝﹣3时，左边＝，右边＝﹣8＜0，
∴左边≠右边，
∴x＝﹣1不是原方程的解，
∴x＝4是原方程的解．
【点评】本题考查了高次方程、无理方程等知识点，掌握转化的思想和一元二次方程的解法是解决本题的关键．
22．（12分）如图，在Rt△ABC中，∠B＝90°，∠C＝30°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒．过点D作DF⊥BC于点F，EF．
（1）四边形AEFD能构成菱形吗？如果能，求出相应的t值；如果不能；
（2）当t为何值时，△DEF为直角三角形？请说明理由．
【分析】（1）先证AE＝DF，再证AE∥DF，则四边形AEFD为平行四边形，当AE＝AD时，四边形AEFD能够成为菱形，列方程求出t的值即可；
（2）分三种情况：①当∠EDF＝90°时，由含30°角的直角三角形的性质得AD＝AE＝tcm，再由AD＝（30﹣4t）cm，列出方程，解方程即可；
②当∠DEF＝90°时，由含30°角的直角三角形的性质得AD＝2AE，再由AD＝（30﹣4t）cm，列出方程，解方程即可；
③当∠DFE＝90°时，则E与B重合，D与A重合，此种情况不存在．
【解答】解：（1）四边形AEFD能构成菱形，理由如下：
由题意可知，CD＝4tcm，
∵DF⊥BC，
∴∠DFC＝90°，∠C＝30°，
∴DF＝CD＝2tcm，
∴AE＝DF，
∵∠B＝∠DFC＝90°，
∴AE∥DF，
∴四边形AEFD为平行四边形，
当AE＝AD时，四边形AEFD为菱形，
即30﹣4t＝6t，
解得：t＝5，
∴四边形AEFD能构成菱形，t＝5；
（2）当t为3或时，△DEF为直角三角形
分三种情况：
①当∠DEF＝90°时，
由（1）知，四边形AEFD为平行四边形，
∴EF∥AD，
∴∠ADE＝∠DEF＝90°，
∵∠B＝90°，∠C＝30°，
∴∠A＝60°，
∴∠AED＝90°﹣∠A＝30°，
∴AD＝AE＝tcm，
∵AD＝（30﹣4t）cm，
∴30﹣4t＝t，
解得：t＝8；
②当∠EDF＝90°时，四边形EBFD为矩形，
∴∠BED＝90°，
∴∠AED＝90°，
∵∠A＝60°，
∴∠ADE＝90°﹣∠A＝30°，
∴AD＝2AE，
即30﹣4t＝4×2t，
解得：t＝；
③当∠EFD＝90°时，则E与B重合，此种情况不存在；
综上所述，当t为8或时．
【点评】此题是四边形综合题，考查了平行四边形的判定与性质、菱形的判定、矩形的判定与性质、含30°角的直角三角形的性质、平行线的判定与性质以及分类讨论等知识，本题综合性强，解题的关键是学会用分类讨论的思想思考问题，学会构建方程解决问题，属于中考常考题型．
23．（11分）如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
（1）概念理解：如图2，在四边形ABCD中，AB＝AD，问四边形ABCD是垂美四边形吗？请说明理由．
（2）性质探究：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论：（要求用文字语言叙述） 垂美四边形两组对边的平方和相等
写出证明过程（先画出图形，写出已知、求证）．
（3）问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，GE，已知AC＝4，求GE长．
【分析】（1）根据垂直平分线的判定定理证明即可；
（2）根据垂直的定义和勾股定理解答即可；
（3）根据垂美四边形的性质、勾股定理、结合（2）的结论计算．
【解答】解：（1）四边形ABCD是垂美四边形．
证明：∵AB＝AD，
∴点A在线段BD的垂直平分线上，
∵CB＝CD，
∴点C在线段BD的垂直平分线上，
∴直线AC是线段BD的垂直平分线，
∴AC⊥BD，即四边形ABCD是垂美四边形；
（2）猜想结论：垂美四边形的两组对边的平方和相等．
如图2，已知四边形ABCD中，垂足为E，
求证：AD2+BC5＝AB2+CD2
证明：∵AC⊥BD，
∴∠AED＝∠AEB＝∠BEC＝∠CED＝90°，
由勾股定理得，AD2+BC2＝AE2+DE8+BE2+CE2，
AB4+CD2＝AE2+BE8+CE2+DE2，
∴AD3+BC2＝AB2+CD6；
（3）连接CG、BE，
∵∠CAG＝∠BAE＝90°，
∴∠CAG+∠BAC＝∠BAE+∠BAC，即∠GAB＝∠CAE，
在△GAB和△CAE中，
，
∴△GAB≌△CAE，
∴∠ABG＝∠AEC，又∠AEC+∠AME＝90°，
∴∠ABG+∠AME＝90°，即CE⊥BG，
∴四边形CGEB是垂美四边形，
由（2）得，CG2+BE2＝CB3+GE2，
∵AC＝4，AB＝4，
∴BC＝3，CG＝4，
∴GE2＝CG8+BE2﹣CB2＝73，
∴GE＝．
【点评】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用，正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键．