山东省济南市章丘区2023-2024学年九年级上学期10月月考数学试题(无答案)

这是一份山东省济南市章丘区2023-2024学年九年级上学期10月月考数学试题(无答案)，共28页。试卷主要包含了方程x，已知关于x的一元二次方程等内容，欢迎下载使用。

本试题分选择题和非选择题两部分，选择题部分共2页，满分为40分；非选择题部分共6页，满分为110分．本试题共8页，满分为150分，考试时间120分钟．本考试不允许使用计算器．
选择题部分共40分
一．选择题（本大题共10小题，每小题4分，共40分．在每个小题给出四个选项中，只有一项符合题目要求）
1．矩形具有而菱形不一定具有的性质是（ ）
A．对角线相等B．对角相等C．对边相等D．对角线互相平分
2．方程x（x－2）=0的解是（ ）
A．x1=x2=－2B．x1=0，x2=2C．x1=0，x2=－2D．无实数根
3．如图，把长方形ABCD沿EF对折，若∠1=50°，则∠AEF的度数等于（ ）
A．65°B．50°C．85°D．115°
4．已知方程2x2－x－1=0的两根分别是x1和x2，则x1+x2的值等于（ ）
A．2B．C．D．－1
5．某公司今年10月的营业额为2500万元，按计划第四季度的总营业额要达到9100万元，求该公司11、12两个月营业额的月均增长率．设该公司11、12两个月营业额的月均增长率为x，则根据题意可列的方程为（ ）
A．2500（1+x）2=9100B．9100（1－x）2=2500
C．2500+2500（1+x）+2500（1+x）2=9100D．9100（1+x）2=2500
6．三角形的两边长分别为3和6，第三边长为方程x2－7x+10=0的一个根，则这个三角形的周长为（ ）
A．11B．11或14C．16D．14
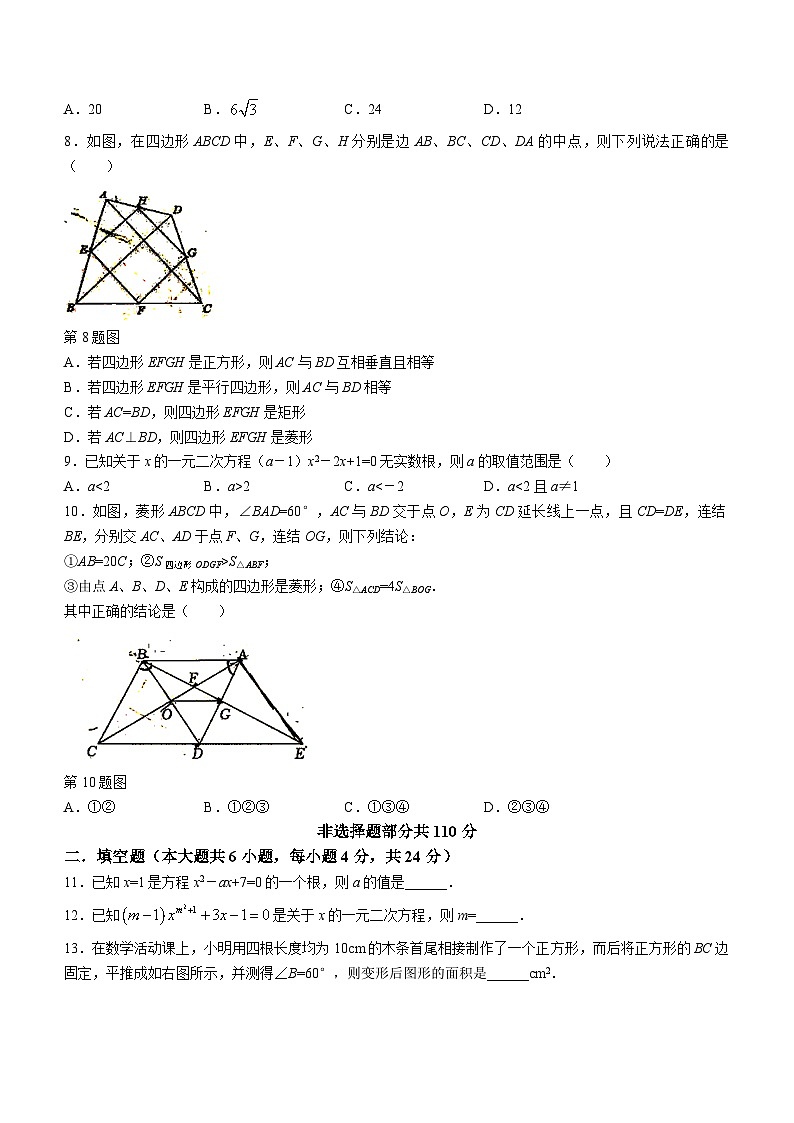
7．如图，在菱形ABCD中，菱形的边长为5，对角线AC的长为8，延长AB至E，BF平分∠CBE，点G是BF上任一点，则△ACG的面积为（ ）
第7题图
A．20B．C．24D．12
8．如图，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA的中点，则下列说法正确的是（ ）
第8题图
A．若四边形EFGH是正方形，则AC与BD互相垂直且相等
B．若四边形EFGH是平行四边形，则AC与BD相等
C．若AC=BD，则四边形EFGH是矩形
D．若AC⊥BD，则四边形EFGH是菱形
9．已知关于x的一元二次方程（a－1）x2－2x+1=0无实数根，则a的取值范围是（ ）
A．a<2B．a>2C．a<－2D．a<2且a≠1
10．如图，菱形ABCD中，∠BAD=60°，AC与BD交于点O，E为CD延长线上一点，且CD=DE，连结BE，分别交AC、AD于点F、G，连结OG，则下列结论：
①AB=20C；②S四边形ODGF>S△ABF；
③由点A、B、D、E构成的四边形是菱形；④S△ACD=4S△BOG．
其中正确的结论是（ ）
第10题图
A．①②B．①②③C．①③④D．②③④
非选择题部分共110分
二．填空题（本大题共6小题，每小题4分，共24分）
11．已知x=1是方程x2－ax+7=0的一个根，则a的值是______．
12．已知是关于x的一元二次方程，则m=______．
13．在数学活动课上，小明用四根长度均为10cm的木条首尾相接制作了一个正方形，而后将正方形的BC边固定，平推成如右图所示，并测得∠B=60°，则变形后图形的面积是______cm2．
第13题图
14．九年级文学小组的同学在举行的图书共享仪式上互赠图书，每名同学都把自己的图书向本组其他成员赠送一本，全组共互赠了132本图书，则全组共有______名同学．
15．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是______．
第15题图
16．如图，Rt△ABC中，∠C=90°，AC=3，BC=4，点P为AB边上任一点，过P分别作PE⊥AC于E，PF⊥BC于F，则线段EF的最小值是______．
第16题图
三．解答题（本大题共10小题，共86分．解答应写出文字说明、证明过程或演算步骤）
17．（本小题满分6分）
解下列方程
（1）x2－6x－5=0（2）（x+3）2=2x+6
18．（本小题满分6分）
已知x=－1是关于x的方程x2－4x+c=0的一个根，求c的值和方程的另一根．
19．（本小题满分6分）
在矩形ABCD中，AB=2cm，BC=8cm，点P从点D出发向点A运动到点A即停止；同时点Q从点B出发向点C运动到点C即停止，点P、Q的速度都是1cm/s，连结PQ、AQ、CP，设点P、Q运动的时间为t秒．
（1）当t为何值时，四边形ABQP是矩形，请说明理由；
（2）当t为何值时，四边形AQCP是菱形，请说明理由．
20．（本小题满分8分）
关于x的一元二次方程x2+2（m－1）x+m2－1=0有两个不相等的实数根x1，x2．
（1）求实数m的取值范围；
（2）是否存在实数m，使得成立？如果存在，求出m的值；如果不存在，请说明理由．
21．（本小题满分8分）
如图，在△ABC中，点D是AB上一点，点E是AC的中点，过点C作．交DE的延长线于点F．
（1）求证：AD=CF；
（2）连接AF，CD．如果点D是AB的中点，那么当△ABC满足______时，四边形ADCF是菱形，请说明理由．
22．（本小题满分8分）
为培养学生正确的劳动价值观和良好的劳动品质，某校为此规划出矩形苗圃ABCD．苗圃的一面靠墙（墙最大可用长度为15米）另三边用木栏围成，中间也用垂直于墙的木栏隔开分成面积相等的两个区域，并在如图所示的两处各留1米宽的门（门不用木栏），修建所用木栏总长28米，设矩形ABCD的一边AB长为x米．
（1）矩形ABCD的另一边BC长为______米（用含x的代数式表示）；
（2）矩形ABCD的面积能否为72m2，若能，请求出AB的长；若不能，请说明理由．
23．（本小题满分10分）
如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作BC的垂线，垂足为点E，延长BC到点F，使CF=BE，连接DF．
（1）求证：四边形AEFD是矩形；
（2）若AB=13，AC=10，求AE的长．
24．（本小题满分10分）
阅读下列材料：利用完全平方公式，将多项式x2+bx+c变形为（x+m）2+n的形式，然后由就可求出多项式x2+bx+c的最小值．
例题：求x2－12x+37的最小值．
解：x2－12x+37=x2－12x+62－62+37=（x－6）2+1．
因为不论x取何值，（x－6）2总是非负数，即．
所以．即当x=6时，x2－12x+37有最小值，最小值是1．
根据上述材料，解答下列问题：
（1）填空：x2－6x+______=（x－_______）2．
（2）将x2+10x－2变形为（x+m）2+n的形式，并求出x2+10x－2的最小值．
（3）如图所示的第一个长方形边长分别是2a+5、3a+2，面积为S1；如图所示的第二个长方形边长分别是5a、a+5，面积为S2．试比较S1与S2的大小，并说明理由．
25．（本小题满分12分）
某商城在2023年端午节期间促销某品牌冰箱，每台进价为2500元，标价为3000元．
（1）商城举行了“新老用户粽是情”摸奖活动，将冰箱连续两次降价，每次降价的百分率相同，最后以每台2430元的价格卖给中奖者，求每次降价的百分率；
（2）经市场调研表明：当每台冰箱的售价为2900元时，平均每天能售出8台，当每台售价每降低50元时，平均每天能多售出4台．若商城要想使该品牌冰箱平均每天的销售利润为5000元，则每台冰箱的售价应定为多少元？
26．（本小题满分12分）
已知四边形ABCD和四边形AEFG均为正方形，连接BE、DG，直线BE与DG交于点H．
图1 图2 备用图
（1）如图1，当点E在AD上时，线段BE和DG的数量关系是_____，∠BHD的度数为_____．
（2）如图2，将正方形AEFG绕点A旋转任意角度．请你判断（1）中的结论是否仍然成立，并说明理由．
（3）若，AE=1，则正方形AEFG绕点A旋转过程中，点F、H是否重合？若能，请直接写出此时线段BG的长；若不能，说明理由．