
初中人教版第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系第1课时教学设计
展开一、教学目标
1.了解直线和圆的位置关系.
2.了解直线与圆的不同位置关系时的有关概念.
3.理解直线和圆的三种位置关系时圆心到直线的距离d和圆的半径r之间的数量关系.
4.会运用直线和圆的三种位置关系的性质与判定进行有关计算.
二、教学重难点
重点:理解直线和圆的三种位置关系时圆心到直线的距离d和圆的半径r之间的数量关系.
难点:直线和圆的三种位置关系的性质与判定的应用.
三、教学过程
【新课导入】
[复习回顾]思考:点和圆的位置关系有几种?(令OP=d )
【新知探究】
直线和圆的三种位置关系
[课件展示]问题1:如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
[归纳总结]
直线和圆有两个公共点,叫做直线和圆相交,这条直线叫圆的割线,这两个点叫交点.
直线和圆有只有一个公共点, 叫做直线和圆相切, 这条直线叫圆的切线,这个点叫切点.
直线和圆没有公共点, 叫做直线和圆相离.
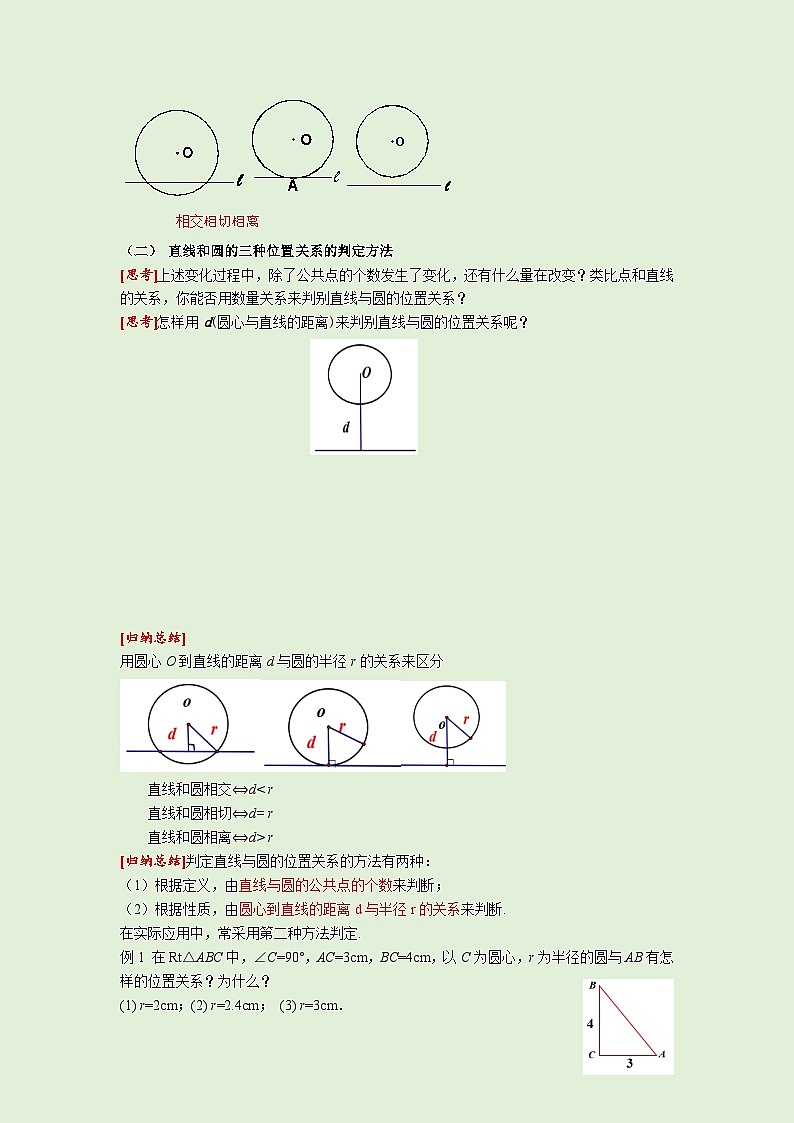
相交相切相离
直线和圆的三种位置关系的判定方法
[思考]上述变化过程中,除了公共点的个数发生了变化,还有什么量在改变?类比点和直线的关系,你能否用数量关系来判别直线与圆的位置关系?
[思考]怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
[归纳总结]
用圆心O到直线的距离d与圆的半径r的关系来区分
直线和圆相交⟺d< r
直线和圆相切⟺d= r
直线和圆相离⟺d> r
[归纳总结]判定直线与圆的位置关系的方法有两种:
(1)根据定义,由直线与圆的公共点的个数来判断;
(2)根据性质,由圆心到直线的距离d与半径r的关系来判断.
在实际应用中,常采用第二种方法判定.
例1 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1) r=2cm;(2) r=2.4cm; (3) r=3cm.
解:过C作CD⊥AB,垂足为D.在△ABC中,
AB=AC2+BC2=32+42=5.
根据三角形的面积公式有12CD×AB=12AC×BC.
∴CD =AC×BCAB=3×45=2.4(cm),即圆心C 到AB 的距离d=2.4cm.
所以 (1)当r=2cm时,有d>r,因此⊙C 和AB 相离.
(2)当r=2.4cm时,有d=r,因此⊙C和AB相切.
(3)当r=3cm时,有d
【课堂训练】
1.看图判断直线l与☉O的位置关系.
(1) (2) (3) (4) (5)
相离相交相交相切相交
2.已知圆的直径为13cm,设直线和圆心的距离为d :
(1)若d=4.5cm ,则直线与圆相交, 直线与圆有2个公共点.
(2)若d=6.5cm ,则直线与圆相切, 直线与圆有1个公共点.
(3)若d= 8 cm ,则直线与圆相离, 直线与圆有0个公共点.
3.已知⊙O的半径为5cm, 圆心O到直线AB的距离为d, 根据条件填写d的范围:
(1)若AB和⊙O相离, 则d > 5cm;
(2)若AB和⊙O相切, 则d = 5cm;
(3)若AB和⊙O相交,则0cm≤d< 5cm.
4.直线l和⊙O有公共点,则直线l与⊙O(D)
A.相离
B.相切
C.相交
D.相切或相交
5. ☉O的半径为5,直线l上的一点到圆心O的距离是5,则直线l与☉O的位置关系是(A)
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
【布置作业】
【教学反思】
教学过程中,强调学生从实际生活中感受,体会直线与圆的几种位置关系,并会用数学语言来描述归纳,经历将实际问题转化为数学问题的过程.
数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆优质教案设计: 这是一份数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆优质教案设计,文件包含2422直线和圆的位置关系第1课时docx、2422直线和圆的位置关系第2课时docx、2422直线和圆的位置关系第3课时docx等3份教案配套教学资源,其中教案共45页, 欢迎下载使用。
人教版九年级上册24.2.2 直线和圆的位置关系公开课第1课时教学设计: 这是一份人教版九年级上册24.2.2 直线和圆的位置关系公开课第1课时教学设计,共6页。教案主要包含了【教材分析】,【教学流程】,【板书设计】,【教后反思】等内容,欢迎下载使用。
人教版九年级上册24.2.2 直线和圆的位置关系第1课时教案: 这是一份人教版九年级上册24.2.2 直线和圆的位置关系第1课时教案,共4页。教案主要包含了教材分析,教学目标,教学重难点,教学过程,板书设计,教学反思等内容,欢迎下载使用。













