初中数学人教版九年级上册24.4 弧长和扇形面积教案

这是一份初中数学人教版九年级上册24.4 弧长和扇形面积教案，共15页。
教学目标
教学目标：
（1）经历探索弧长和扇形面积公式的过程，培养学生的探索能力，会利用弧长和扇形面积计算公式解决问题.
（2）在弧长和扇形面积计算公式的探究过程中，理解局部与整体之间的关系，感受转化、类比的数学思想.
（3）体验数学与人类生活的密切联系，激发学生学习数学的兴趣，提高他们的学习积极性.
教学重难点
教学重点：弧长公式及扇形面积公式的推导和应用
教学难点：弧长公式及扇形面积公式的推导
教学过程
时间
教学环节
主要师生活动
00:00-01:37
情景引入
提出问题
熊大、熊二、吉吉要给光头强过生日，他们4人要平分一块蛋糕，熊二自告奋勇切蛋糕，因为熊二没有分均匀，被惩罚最后选蛋糕，光头强选择了最大的，熊大选择了第二块，吉吉选择了第三块，熊二选择了最小的.
后来，光头强将自己的蛋糕又分了一下，把这一块半圆分给3个伙伴.
切蛋糕时，切出来这的几部分都叫做扇形，像展开的扇子。这块大的虽然不太像扇子，但它也是扇形，同学们熟悉的半圆也是特殊的扇形。在生活中，切西瓜、切大饼也可以产生扇形，校园里的银杏叶也是扇形.
扇形是独特的平面图形，它是由线段和曲线共同围成的图形。围成扇形的曲线，也就是弧，弧的长度引起了人们的兴趣，扇形的面积也是让人着迷的问题.
课前预习
1.扇形的概念：
由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形．半圆是（是/不是）扇形．
2.生活中的扇形十分常见，如扇形蛋糕、银杏叶扇形盘子、扇形西瓜、扇贝壳、孔雀开屏、扇形统计图、扇形置物架等．请试举一例.
设计意图：感受数学与人类生活的密切联系，激发学生学习数学的兴趣，提高他们的学习积极性.
01:37-03:24
问题探究一
要研究扇形的弧长和面积公式，首先请出两个祖师爷公式，圆的周长和圆的面积公式.
学生思考，能容易回答出圆的周长和圆的面积公式.
展示：圆的周长=2πR和圆的面积=πR2
这两个公式都是小学已经学过的，大家都已经比较熟悉了。如何通过这两个公式找到计算弧长和扇形面积的方法呢？
思考：如果让你切蛋糕，平分给4个人，你如何切呢？
将蛋糕切成2个半圆，每个半圆的面积就是圆面积的12，也就有
S=12S圆=12πR2，再把两个半圆，切为圆心角为90°的扇形，每个扇形的面积就是圆面积的14，也就有S=14S圆=14πR2.
细心的同学发现，要求扇形的面积，要知道圆的面积和扇形与圆的比。同样，要计算弧长，就要知道圆的周长和弧与圆周的比。
要知道圆的面积和圆的周长，知道圆的半径R就可以了，那这个比怎么知道呢？想想刚刚的平分到的蛋糕为什么是圆的14？
学生思考，因为圆所对应的圆心角是360°，这个扇形所对的圆心角是90°，，也就是扇形或者弧所对圆心角与360°的比.
设圆心角为n°，比例：
弧长l=圆周长×=2πR×=
扇形面积S扇形=圆面积×==
找到半径R和圆心角n就可以计算弧长和扇形面积
设计意图：从特殊到一般，教师引导学生抓住弧长和圆周长的比例关系来推导公式；教师对弧长公式进行解析，使学生更加清楚公式中涉及到的量.
03:24-04:00
公式的直接应用：练习
学生独立解决以下问题：
练习：
1.半径为2的圆中，120°的圆心角所对的弧长是多少？
弧长l=圆周长×=2πR×=
是准确值，3.14是近似值
除非题中告诉要取近似值，否则最后的答案写.
2.半径为2的圆中，一段弧长为2π的弧，求它所对的圆心角的度数.
∵l=2πR×=2π,R=2
∴2π×2×=2π
∴n=180
设计意图：熟悉弧长公式
04:00-04:34
公式在生活中的应用
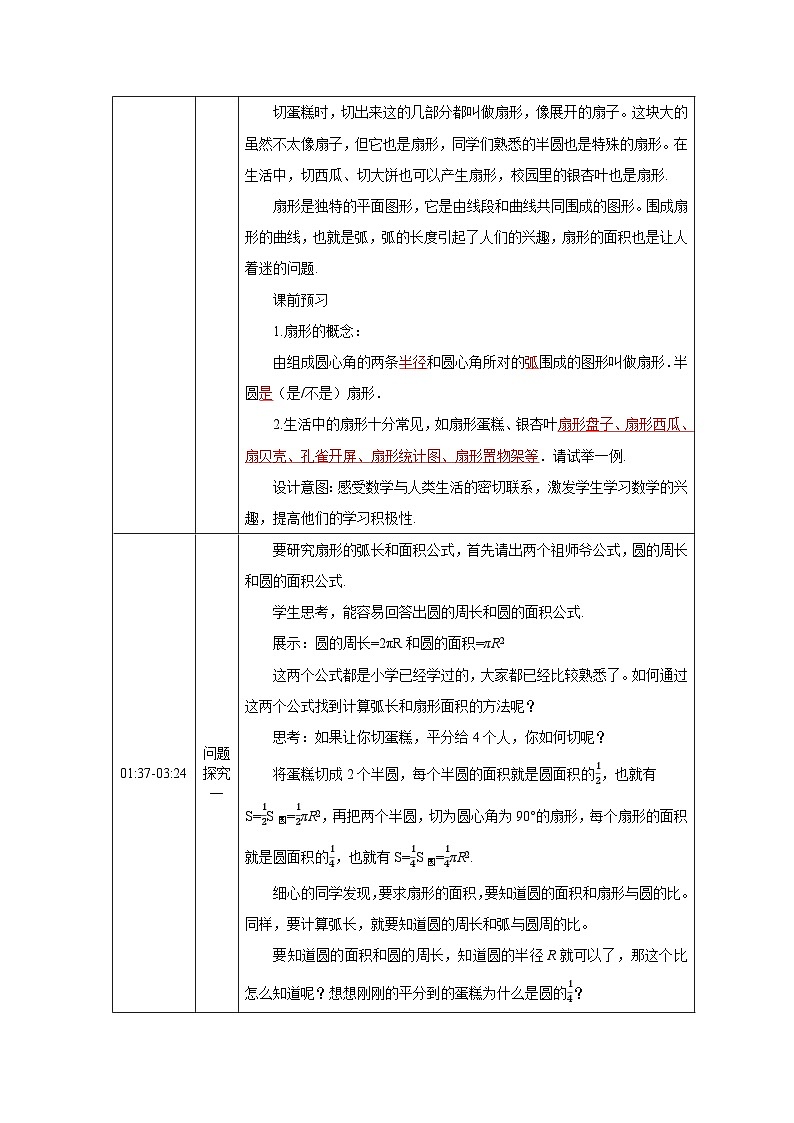
例1.制造弯形管道时，要先按中心线计算“展直长度”，
再下料，试计算图所示管道的展直长度L.(结果取整数)
要这个弯形管道的展直长度包括哪些部分？
分析：管道的展直长度 L=AC的长+BD的长+弧AB的长
解：由弧长公式l=，得弧AB的长
l==500π（mm）
∴所求的展直长度
L=2×700+1570=2970（mm）
答：管道的展直长度约为2970mm.
设计意图：应用弧长公式解决实际生活中的问题
04:34-05:12
问题探究二
我们已经知道：
弧长l=圆周长×=2πR×=
扇形面积S扇形=圆面积×==
S是扇形面积，R是半径，n是扇形圆心角的度数.
思考：观察扇形面积与弧长公式, 能不能用弧长表示扇形面积？
S扇形=====
求扇形面积，已知半径R和圆心角n,用公式一 S扇形=
已知半径R和弧长l,用公式二 S扇形=
设计意图：探索扇形面积与弧长的关系，推导扇形面积公式.
05:12-05:37
公式的直接应用：练习
学生独立解决以下问题：
1. 已知扇形的圆心角为120°，半径为2，则这个扇形的面积等于多少？
S扇形==
2. 已知扇形面积为π，圆心角为60°，则这个扇形的半径R等于多少？
∵S扇形=
∴π=
∴
又∵R＞0
∴R=
3. 已知半径为2的扇形，其弧长为π，则这个扇形的圆心角为多少度？
S扇形===π
设计意图：熟悉扇形面积公式
未讲
公式在生活中的应用
例3. 如图,水平放置的圆柱形排水管道的截面半径是0.6m，其中水面高0.3m，求截面上有水部分的面积.（精确到0.01m2）
把文字语言和图形语言对应起来，排水管道的截面就是图中的圆.把已知条件转化成几何元素标在图上.
分析：所求面积= S扇形OAB－ S△OAB
解：
连接OA，OB，作OC⊥AB，垂足为D，
交弧AB于点C，连接AC
∵ OC=0.6，DC=0.3
∴ OD= OC－DC=0.3
∴ OD= DC=0.3
又 ∵ OC⊥AB即AD⊥OC
∴ AD垂直平分OC
∴ AC=AO=OC=0.6
∴△OAC为等边三角形
∴∠AOD=60°
又∵△OAB中，OA=OB
∴∠AOB=2∠AOD=120°.
在Rt△OAD中，根据勾股定理，得
AD===
∴AB=2AD=
有水部分的面积
S = S扇形OAB－ S△OAB
=
=
=
≈0.22（m2）
05:37-05:46
课堂小结
最后，总结本节课所学.
1.弧长公式和扇形面积公式，求解的关键是半径R和圆心角n.
弧长l=圆周长×=
扇形面积S扇形=圆面积×=
2.扇形面积与弧长的关系：S扇形=
05:46-05:52
布置作业
课后练习
1.已知扇形的圆心角为120°，半径为6，则扇形的弧长是（ ）．
A．3 B．4 C．5 D．6
2．如图所示，把边长为2的正方形ABCD的一边放在定直线L上，按顺时针方向绕点D旋转到如图的位置，则点B运动到点B′所经过的路线长度为_____.
3. 如图，在正方形ABCD中，分别以B，D为圆心，以正方形的边长a为画弧，形成树叶形(阴影部分)图案，则树叶形图案的面积为_________.