江苏省泰州市兴化市2023—-2024学年九年级上学期学生评价数学A卷试题

这是一份江苏省泰州市兴化市2023—-2024学年九年级上学期学生评价数学A卷试题，文件包含湖南师大附中数学附中3次pdf、湖南师大附中数学答案附中3次pdf等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。
一、选择题（本大题共有4题，每小题3分，共12分）
二、填空题（本大题共有8题，每小题3分，共24分）
5． （1，2） 6． 九
7． 90 8． 2
9． 10． 40、70、100
11． 12． 18
三、解答题（本大题共有9题，共78分．解答时应写出必要的步骤）
13．⑴ ， ………………………………4分
注：用配方法解方程，用其他方法不得分！
⑵ ， ………………………………4分


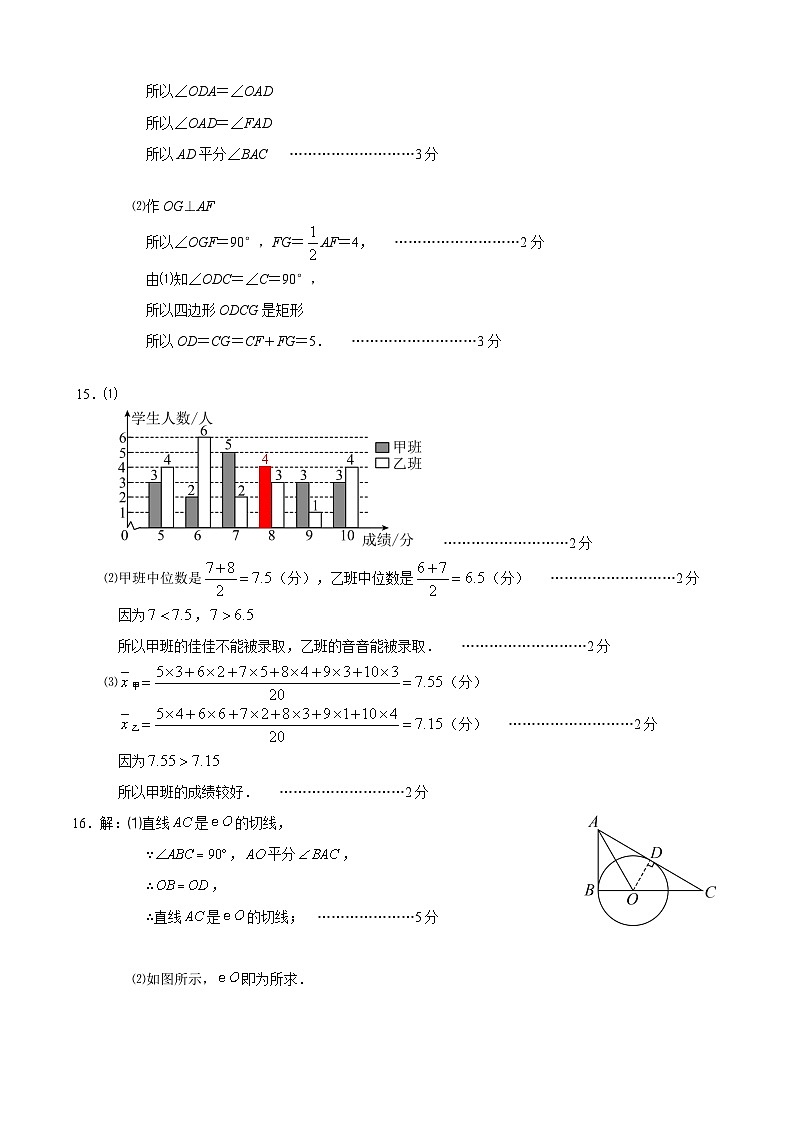
14．解：⑴连接OD
因为BC是⊙O的切线
所以∠ODB＝90°
又因为∠C＝90°
所以∠ODB＝∠C
所以OD∥AC ………………………2分
所以∠ODA＝∠FAD
因为OD＝OA
所以∠ODA＝∠OAD
所以∠OAD＝∠FAD
所以AD平分∠BAC ………………………3分
⑵作OG⊥AF
所以∠OGF＝90°，FG＝AF＝4， ………………………2分
由⑴知∠ODC＝∠C＝90°，
所以四边形ODCG是矩形
所以OD＝CG＝CF＋FG＝5． ………………………3分
15．⑴
4
………………………2分
⑵甲班中位数是（分），乙班中位数是（分） ………………………2分
因为，
所以甲班的佳佳不能被录取，乙班的音音能被录取． ………………………2分
⑶甲（分）
乙（分） ………………………2分
因为
所以甲班的成绩较好． ………………………2分
16．解：⑴直线是的切线，
∵，平分，
∴，
∴直线是的切线； …………………5分
⑵如图所示，即为所求．
……………………5分
17．解：⑴

∵，即
∴方程总有两个实数根 ……………………3分
⑵由⑴知
∴
∴，
∵方程有一个根是负数
∴
∴
又∵m是正整数
∴m＝1或2或3 ……………………3分
⑶由⑵知，
①当4为底边时，
∵
∴等腰三角形不存在，舍去
②当4为腰时，，即
∵
∴等腰三角形存在
综上所述，m的值为8 ……………………4分
18．⑴设年平均增长率为x
则
得，（舍去）
故年平均增长率为50% ………………………4分
⑵设房价定为m元
则
得，
∵让游客享受更低的单价
∴m＝230
故房价定为230元 ………………………6分
Q
B
O
A
P
H
C
Q
B
O
A
P
F
E
B
O
A
P
图2
图3
图1
19．
N
E
M
H
⑴连接OQ
∵ 折叠
∴ AO=AQ
又∵ AO=OQ
∴ AO=OQ=AQ
∴ △AOQ为正三角形
∴ ∠AOQ=60°
∴ ∠BOQ=30°
∴ ………………………3分
（2）过点O作OM⊥AC于点M
由垂径定理可得AC=2AM
根据AAS可得△AOM≌AQH
∴AM=AH
∴AC=16 ………………………4分
(3)点O的对称点N,过N作NH⊥AO于点H,过点P作PE⊥NH于点E
在中由垂径定理可得AF=2AM
可得AM=8 , OM=5
在Rt△AMN中由勾股定理得MN=
设PO= x
在Rt△PEN中由勾股定理得 得
………………………5分
20．
（1）①M(1,4) ………………………4分
②根据二次函数解析式得B(3,0)，C（0，3）
可得直线BC函数表达式y=-x+3
设点E( t,0 )
∵点E在OB上运动
∴0＜t＜3
∵PF=12EF
∴
∴
∴ ………………………4分
（2）平行，理由如下：
设E( t,0 )
顶点
直线PM函数表达式：
∴
直线EQ函数表达式：
点
直线BM函数表达式：
∴EQ∥BM ………………………6分题号
1
2
3
4
答案
A
A
D
C