第六章 反比例函数 单元检测卷（B卷）-2023-2024学年九年级数学上册《同步考点解读•专题训练》（北师大版）

这是一份第六章 反比例函数 单元检测卷（B卷）-2023-2024学年九年级数学上册《同步考点解读•专题训练》（北师大版），文件包含湖南师大附中数学附中3次pdf、湖南师大附中数学答案附中3次pdf等2份试卷配套教学资源，其中试卷共14页， 欢迎下载使用。

选择题（本题共10小题，每小题3分，共30分）。
1．下列函数关系式中不是表示反比例函数的是（ ）
A．xy＝5B．y＝C．y＝﹣3x﹣1D．y＝
【答案】D
【解答】解：A、是反比例函数，错误；
B、是反比例函数，错误；
C、是反比例函数，错误；
D、不是反比例函数，正确．
故选：D．
2．已知点（3，﹣1）是双曲线y＝（k≠0）上的一点，则下列各点不在该双曲线上的是（ ）
A．（，﹣9）B．（6，﹣）C．（﹣1，3）D．（3，1）
【答案】D
【解答】解：因为点（3，﹣1）是双曲线y＝（k≠0）上的一点，将（3，﹣1）代入y＝（k≠0），得k＝﹣3；四个选项中只有D不符合要求：k＝3×1≠﹣3．
故选：D．
3.如果反比例函数的图象经过点P（﹣2，﹣1），那么这个反比例函数的表达式为（ ）
A．B．C．D．
【答案】C
【解答】解：设y＝，将点（﹣2，﹣1）代入解析式可得，k＝2，所以y＝．
故选：C．
4．若一次函数y＝kx+b与反比例函数的图象都经过点（﹣2，1），则b的值是（ ）
A．3B．﹣3C．5D．﹣5
【答案】B
【解答】解：将点（﹣2，1）代入解析式，得k＝﹣2；
再把点（﹣2，1）和k＝﹣2代入一次函数，得
﹣2×（﹣2）+b＝1，
解得b＝﹣3．
故选：B．
5．如果矩形的面积为6cm2，那么它的长ycm与宽xcm之间的函数关系用图象表示大致是（ ）
A．B．
C．D．
【答案】C
【解答】解：由矩形的面积公式可得xy＝6，
∴y＝（x＞0，y＞0）．图象在第一象限．
故选：C
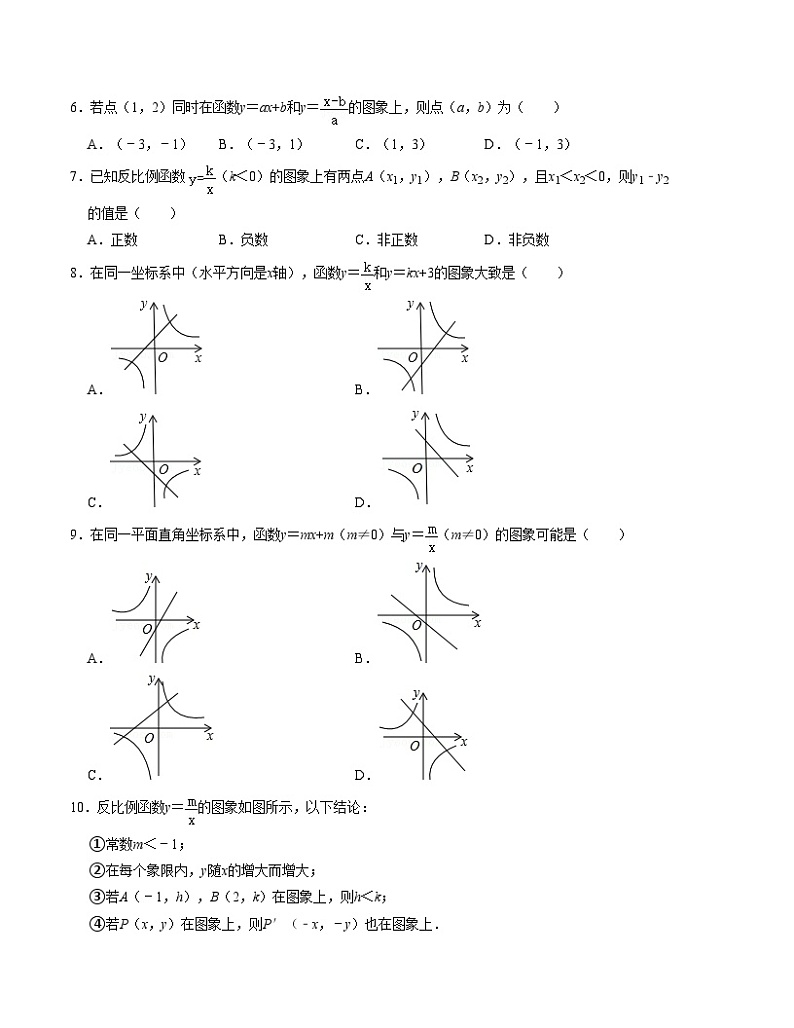
6．若点（1，2）同时在函数y＝ax+b和y＝的图象上，则点（a，b）为（ ）
A．（﹣3，﹣1）B．（﹣3，1）C．（1，3）D．（﹣1，3）
【答案】D
【解答】解：依题意可得，
解得．
故选：D．
7．已知反比例函数（k＜0）的图象上有两点A（x1，y1），B（x2，y2），且x1＜x2＜0，则y1﹣y2的值是（ ）
A．正数B．负数C．非正数D．非负数
【答案】B
【解答】解：∵k＜0，
∴反比例函数的图象在二、四象限，
又∵A（x1，y1），B（x2，y2）中，x1＜x2＜0，
∴A、B两点在第二象限，y1＜y2，
即y1﹣y2＜0．
故选：B．
8．在同一坐标系中（水平方向是x轴），函数y＝和y＝kx+3的图象大致是（ ）
A．B．
C．D．
【答案】A
【解答】解：A、由函数y＝的图象可知k＞0与y＝kx+3的图象k＞0一致，故A选项正确；
B、因为y＝kx+3的图象交y轴于正半轴，故B选项错误；
C、因为y＝kx+3的图象交y轴于正半轴，故C选项错误；
D、由函数y＝的图象可知k＞0与y＝kx+3的图象k＜0矛盾，故D选项错误．
故选：A．
9．在同一平面直角坐标系中，函数y＝mx+m（m≠0）与y＝（m≠0）的图象可能是（ ）
A．B．
C．D．
【答案】C
【解答】解：A、由反比例函数图象得m＜0，则一次函数图象经过第二、三、四象限，所以A选项错误；
B、由反比例函数图象得m＞0，则一次函数图象经过第一、二、三象限，所以B选项错误；
C、由反比例函数图象得m＞0，则一次函数图象经过第一、二、三象限，所以C选项正确；
D、由反比例函数图象得m＜0，则一次函数图象经过第二、三、四象限，所以D选项错误．
故选：C
10．反比例函数y＝的图象如图所示，以下结论：
①常数m＜﹣1；
②在每个象限内，y随x的增大而增大；
③若A（﹣1，h），B（2，k）在图象上，则h＜k；
④若P（x，y）在图象上，则P′（﹣x，﹣y）也在图象上．
其中正确的是（ ）
A．①②B．②③C．③④D．①④
【答案】C
【解答】解：∵反比例函数的图象位于一三象限，
∴m＞0
故①错误；
当反比例函数的图象位于一三象限时，在每一象限内，y随x的增大而减小，故②错误；
将A（﹣1，h），B（2，k）代入y＝得到h＝﹣m，2k＝m，
∵m＞0
∴h＜k
故③正确；
将P（x，y）代入y＝得到m＝xy，将P′（﹣x，﹣y）代入y＝得到m＝xy，
故P（x，y）在图象上，则P′（﹣x，﹣y）也在图象上
故④正确，
故选：C．
二．填空题（本共6小题，每小题3分，共18分）。
11．在某一电路中，保持电压不变，电阻R（欧）与电流I（安）成反比例，其图象如图所示，则这一电路中的电压为 伏．
【答案】12
【解答】解：由题意可知：保持电压不变，电阻R（欧）与电流I（安）成反比例，
设R＝，即U＝IR，
由图象上的一点坐标为（2，6），即I＝2（安），R＝6（欧），
∴U＝2×6＝12（伏）．
故答案为：12
12．反比例函数y＝的图象经过点（1，﹣2），则k的值为 ．
【答案】﹣2
【解答】解：∵反比例函数y＝的图象经过点（1，﹣2），
∴＝﹣2，
解得k＝﹣2．
故答案为：﹣2．
13．已知函数y＝（k+1）（k为整数），当k为 时，y是x的反比例函数．
【答案】0
【解答】解：∵y＝（k+1）是反比例函数，
∴，
解之得k＝0．
14．当 时，函数y＝的图象所在的象限内，y随x的增大而增大．
【答案】m＜1
【解答】解：∵函数y＝的图象所在的象限内，y随x的增大而增大，
∴m﹣1＜0，
即m＜1．
故答案为：m＜1．
15．如图，在Rt△ABC中，∠C＝90°，AC＝BC，BC∥x轴，点A、B都在反比例函数y＝上，点C在反比例函数y＝上，则AB＝ ．
【答案】3
【解答】解：设C（a，），AC＝BC＝m，
∴A（a，+m），B（a+m，），
∵点A、B都在反比例函数y＝上，
∴a（+m）＝（a+m）•＝10，
解得m＝3，
∴AC＝BC＝3，
在Rt△ABC中，AB＝＝3，
故答案为3．
16．如图，在平面直角坐标系中，Rt△ABC的顶点A，C的坐标分别是（0，3），（3，0）．∠ACB＝90°，AC＝2BC，则函数y＝（k＞0，x＞0）的图象经过点B，则k的值为 ．
【答案】
【解答】解：过B点作BD⊥x轴于D，如图，
∵A，C的坐标分别是（0，3），（3，0）．
∴OA＝OC＝3，
∴△OAC为等腰直角三角形，
∴AC＝OC＝3，∠ACO＝45°，
∵∠ACB＝90°，
∴∠BCD＝45°，
∵△BCD为等腰直角三角形，
∴CD＝BD＝BC，
∵AC＝2BC，
∴BC＝，
∴CD＝BD＝×＝，
∴OD＝3+＝，
∴B（，），
∵函数y＝（k＞0，x＞0）的图象经过点B，
∴k＝×＝．
故答案为．
三、解答题（本题共6题，17题6分，18题8分，19题10分，20-21题12分）。
17．反比例函数的图象过点（2，﹣2）．
（1）求反比例函数y与自变量x之间的关系式，它的图象在第几象限内？
（2）y随x的减小如何变化？
（3）试判断点（﹣3，0），（﹣3，﹣3）是否在此函数图象上？
【解答】解：（1）设y＝，
把（2，﹣2）代入得k＝2×（﹣2）＝﹣4，
所以反比例函数y与自变量x之间的关系式为y＝﹣，它的图象在第二、四象限；
（2）在每一象限内，y随x的减小而减小；
（3）因为﹣3×0＝0，﹣3×（﹣3）＝9，
所以点（﹣3，0），（﹣3，﹣3）都不在在此函数图象上．
18．已知如图，一次函数y＝kx+b的图象与反比例函数的图象相交于A、B两点．
（1）利用图中条件，求反比例函数和一次函数的解析式；
（2）根据图象写出使一次函数的值大于反比例函数的值的x的取值范围．
【解答】解：（1）据题意，反比例函数的图象经过点A（﹣2，1），
∴有m＝xy＝﹣2
∴反比例函数解析式为y＝﹣，
又反比例函数的图象经过点B（1，n）
∴n＝﹣2，
∴B（1，﹣2）
将A、B两点代入y＝kx+b，有，
解得，
∴一次函数的解析式为y＝﹣x﹣1，
（2）一次函数的值大于反比例函数的值时，
x取相同值，一次函数图象在反比例函数上方即一次函数大于反比例函数，
∴x＜﹣2或0＜x＜1，
19．如图，一次函数y＝﹣x+4的图象与反比例函数y＝（k为常数，且k≠0）的图象交于A（1，a），B两点．
（1）求反比例函数的表达式及点B的坐标；
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．
【解答】解：（1）把点A（1，a）代入一次函数y＝﹣x+4，
得：a＝﹣1+4，解得：a＝3，
∴点A的坐标为（1，3）．
把点A（1，3）代入反比例函数y＝，
得：3＝k，
∴反比例函数的表达式y＝，
联立两个函数关系式成方程组得：，
解得：，或，
∴点B的坐标为（3，1）．
（2）作点B作关于x轴的对称点D，交x轴于点C，连接AD，交x轴于点P，此时PA+PB的值最小，连接PB，如图所示．
∵点B、D关于x轴对称，点B的坐标为（3，1），
∴点D的坐标为（3，﹣1）．
设直线AD的解析式为y＝mx+n，
把A，D两点代入得：，
解得：，
∴直线AD的解析式为y＝﹣2x+5．
令y＝﹣2x+5中y＝0，则﹣2x+5＝0，
解得：x＝，
∴点P的坐标为（，0）．
S△PAB＝S△ABD﹣S△PBD＝BD•（xB﹣xA）﹣BD•（xB﹣xP）＝×[1﹣（﹣1）]×（3﹣1）﹣×[1﹣（﹣1）]×（3﹣）＝．
20.某商场出售一批进价为2元的贺卡，在市场营销中发现，此商品的日销售单价x（单位：元）与日销售数量y（单位：张）之间有如下关系：
（1）根据表中数据在平面直角坐标系中描出实数对（x，y）的对应点；
（2）确定y与x之间的函数关系式，并画出图象；
（3）设销售此贺卡的日纯利润为w元，试求出w与x之间的函数关系式．若物价局规定该贺卡售价最高不超过10元/张，请你求出日销售单价x定为多少元时，才能获得最大日销售利润？
【解答】解：（1）如图，直接建立坐标系描点即可．
（2）如图所示：
设函数关系式为y＝（k≠0且k为常数），
把点（3，20）代入y＝中得，
k＝60，
又将（4，15）（5，12）（6，10）分别代入，成立．
所以y与x之间的函数关系式为：．
（3）∵，
则函数是增函数在x＞0的范围内是增函数，
又∵x≤10，
∴当x＝10，W最大，
∴此时获得最大日销售利润为48元．
21．如图，点B（3，3）在双曲线y＝（x＞0）上，点D在双曲线y＝﹣（x＜0）上，点A和点C分别在x轴，y轴的正半轴上，且点A，B，C，D构成的四边形为正方形．
（1）求k的值；
（2）求点A的坐标．
【解答】解：（1）∵点B（3，3）在双曲线y＝上，
∴k＝3×3＝9；
（2）∵B（3，3），
∴BN＝ON＝3，
设MD＝a，OM＝b，
∵D在双曲线y＝﹣（x＜0）上，
∴ab＝4，
过D作DM⊥x轴于M，过B作BN⊥x轴于N，
则∠DMA＝∠ANB＝90°，
∵四边形ABCD是正方形，
∴∠DAB＝90°，AD＝AB，
∴∠MDA+∠DAM＝90°，∠DAM+∠BAN＝90°，
∴∠ADM＝∠BAN，
在△ADM和△BAN中，
，
∴△ADM≌△BAN（AAS），
∴BN＝AM＝3，DM＝AN＝a，
∴0A＝3﹣a，
即AM＝b+3﹣a＝3，
a＝b，
∵ab＝4，
∴a＝b＝2，
∴OA＝3﹣2＝1，
即点A的坐标是（1，0）．
销售单价x（元）
3
4
5
6
日销售量y（张）
20
15
12
10