北师大版五年级数学上册期中高频易错题综合检测卷三

这是一份北师大版五年级数学上册期中高频易错题综合检测卷三，共43页。试卷主要包含了选择题，填空题，判断题，计算题，作图题，解答题等内容，欢迎下载使用。
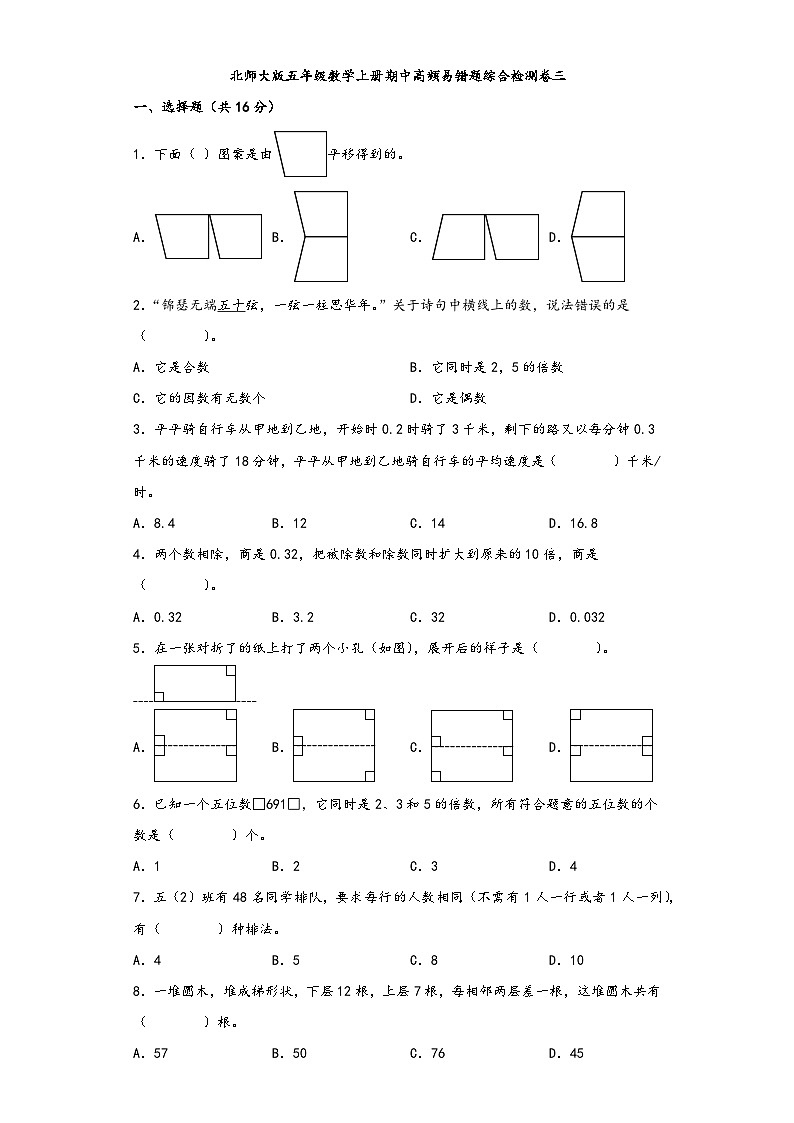
1．下面（ ）图案是由平移得到的。
A．B．C．D．
2．“锦瑟无端五十弦，一弦一柱思华年。”关于诗句中横线上的数，说法错误的是（ ）。
A．它是合数B．它同时是2，5的倍数
C．它的因数有无数个D．它是偶数
3．平平骑自行车从甲地到乙地，开始时0.2时骑了3千米，剩下的路又以每分钟0.3千米的速度骑了18分钟，平平从甲地到乙地骑自行车的平均速度是（ ）千米/时。
A．8.4B．12C．14D．16.8
4．两个数相除，商是0.32，把被除数和除数同时扩大到原来的10倍，商是（ ）。
A．0.32B．3.2C．32D．0.032
5．在一张对折了的纸上打了两个小孔（如图），展开后的样子是（ ）。
A．B．C．D．
6．已知一个五位数□691□，它同时是2、3和5的倍数，所有符合题意的五位数的个数是（ ）个。
A．1B．2C．3D．4
7．五（2）班有48名同学排队，要求每行的人数相同（不需有1人一行或者1人一列），有（ ）种排法。
A．4B．5C．8D．10
8．一堆圆木，堆成梯形状，下层12根，上层7根，每相邻两层差一根，这堆圆木共有（ ）根。
A．57B．50C．76D．45
二、填空题（共16分）
9．一个梯形的面积是22.5平方分米，高是5分米，下底是7分米，上底是( )分米。
10．下图是一个( )图形，它有( )条对称轴。
11．童装厂有50米布，做一套校服用布2米，可以做( )套；如果每套校服用布2.2米，这些布可以做( )套。
12．看图回答问题。
下图图形1向( )平移( )格得到图形2。
13．已知3个连续偶数的和是48，这3个偶数中最大的是( )，最小的偶数是( )。
14．一个质数（两位数）的个位上的数字与十位上的数字交换位置后，变成7的倍数，这样的质数有( )。
15．一块平行四边形木板，底长5.8厘米，比高少2.2厘米，它的面积是( )平方厘米。
16．小明买了3千克梨和3千克苹果，共付了60.3元，小芳买了同样的1千克梨和3千克苹果，共付了45.3元，平均每千克苹果( )元。
三、判断题（共8分）
17．如图，这个安全标记是轴对称图形。( )
18．一个平行四边形相邻两边的长度分别是15厘米和9厘米，已知一条边上的高是10厘米，这个平行四边形的面积是90平方厘米。( )
19．小数除以小数，商一定大于被除数。( )
20．五个连续自然数的和不是奇数就是偶数。( )
四、计算题（共18分）
21．（6分）列竖式计算，打★的要验算。
16.8÷16＝ ★21.56÷5.6＝ 5.4÷3.5≈（结果保留两位小数）
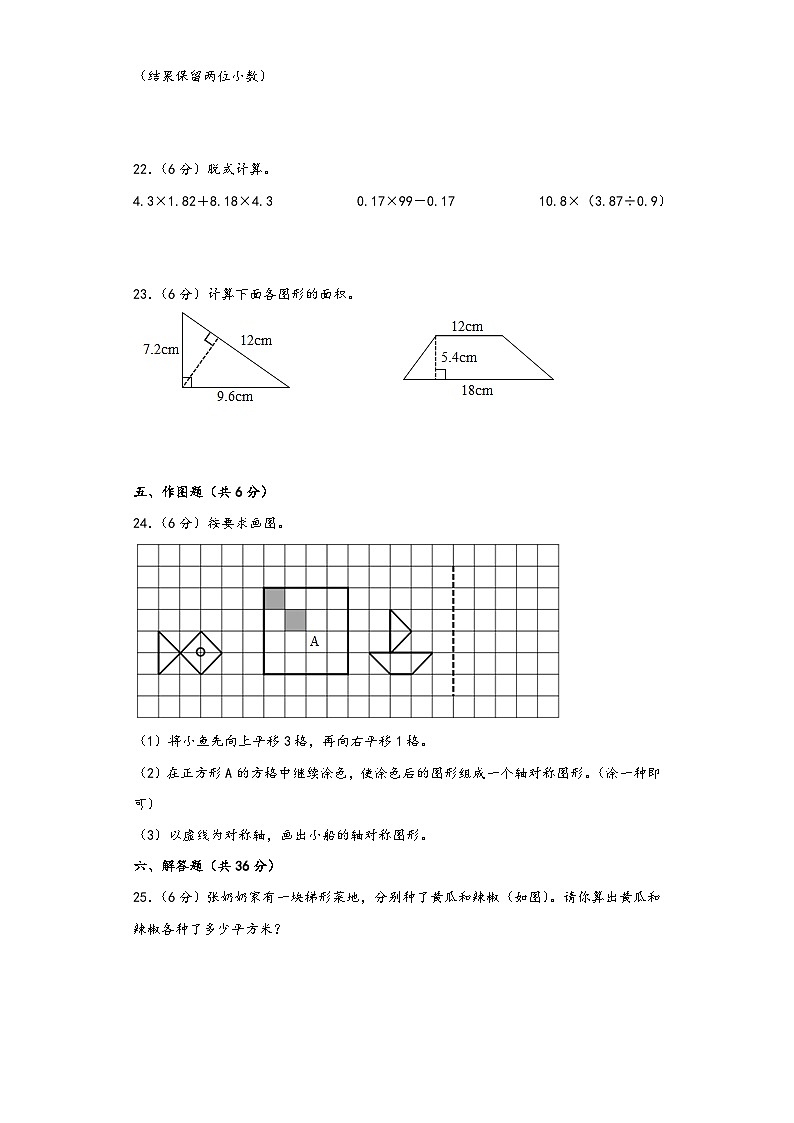
22．（6分）脱式计算。
4.3×1.82＋8.18×4.3 0.17×99－0.17 10.8×（3.87÷0.9）
23．（6分）计算下面各图形的面积。
五、作图题（共6分）
24．（6分）按要求画图。
（1）将小鱼先向上平移3格，再向右平移1格。
（2）在正方形A的方格中继续涂色，使涂色后的图形组成一个轴对称图形。（涂一种即可）
（3）以虚线为对称轴，画出小船的轴对称图形。
六、解答题（共36分）
25．（6分）张奶奶家有一块梯形菜地，分别种了黄瓜和辣椒（如图）。请你算出黄瓜和辣椒各种了多少平方米？

26．（6分）
27．（6分）莎莉文面包房运来65个面包，如果每3个装一袋，能正好装完吗？如果每5个装一袋，能正好装完吗？为什么？
28．（6分）北京世界园艺博览会中，中国馆作为核心景观区，不仅外形亮服，它还是一座“会呼吸”“有生命”的绿色建筑。中国馆的钢结构屋盖安装有块光伏玻璃。是一个四位数，其中A既不是质数，也不是合数；B是最小的偶数；C是最小的质数；D是最小的合数。一共安装了多少块光伏玻璃？
29．（6分）铁路小学食堂制作一种蛋糕，每个蛋糕需要面粉0.35千克，王师傅买了39千克面粉，最多能做多少个这样的蛋糕？
30．（6分）一块平行四边形菜地，底20米，高12米，如果每平方米收青菜7.5千克，这块菜地共收青菜多少千克？
参考答案
1．A
【分析】平移：在平面内，将一个图形上的所有点都按照某个方向作相同距离移动的图形运动；平移后图形的位置改变，形状、大小、方向不变；据此解答即可。
【详解】根据平移的特征，可得A是由原图形平移得到的图案。
故答案为：A
【点睛】此题考查了平移的意义。
2．C
【分析】除了1和它本身以外还有其他因数，这样的数叫合数。
既是2的倍数又是5的倍数的特征：个位上的数字是0的数，既是2的倍数，又是5的倍数。
一个数的因数的个数是有限的，最小的因数是1，最大的因数是它本身。
整数中，是2的倍数的数叫偶数，不是2的倍数的数叫奇数。
【详解】横线上的数写作：50
A．50是合数，选项说法正确；
B．50既是2的倍数也是5的倍数，选项说法正确；
C．一个数的因数个数是有限的，选项说法错误；
D．50是偶数，选项说法正确。
说法错误的是它的因数有无数个。
故答案为：C
【点睛】本题考查的知识点较多，要综合运用所学知识。
3．D
【分析】根据距离＝速度×时间，代入数据，求出剩下的路的距离，用0.3×18，再加上0.2时骑的距离，求出甲地到乙地的总距离；再根据速度＝距离÷时间，代入数据，求出平均速度，即可解答。
【详解】0.3×18＝5.4（千米）
18分钟＝0.3时
（3＋5.4）÷（0.2＋0.3）
＝8.4÷0.5
＝16.8（千米/时）
故答案为：D
【点睛】利用速度、时间和距离三者的关系进行解答，注意单位名数的换算。
4．A
【分析】被除数和除数同时乘或除以一个不为0的数，商的大小不变；依此选择。
【详解】两个数相除，商是0.32，把被除数和除数同时扩大到原来的10倍，商仍然是0.32；
故答案为：A
【点睛】熟练掌握商的变化规律是解答此题的关键。
5．B
【分析】在一张对折了的纸上打了两个小孔，展开后的样子应该是一个关于虚线对称的图形，据此解答。
【详解】由分析可知，关于虚线对称的图形是。
故选择：B
【点睛】此题考查了补全轴对称图形，明确如果一个图形沿一条直线对折，两边部分能够完全重合，这个图形就是轴对称图形。
6．C
【分析】2的倍数特征：末尾是0、2、4、6、8的数是2的倍数；5的倍数特征：末尾是0、5的数是5的倍数，3的倍数特征：各个数位上的数字的和是3的倍数，这个数就是3的倍数，由于这个数同时是2、3、5的倍数，那么个位上是0，之后根据3的倍数特征找出万位的数即可。
【详解】由分析可知：
个位上的数是0
6＋9＋1＋0＝16
16＋2＝18
16＋5＝21
16＋8＝24
所以这个五位数可以是：26910、56910、86910；共3个。
故答案为：C
【点睛】本题主要考查2、3、5的倍数特征，熟练掌握它们的特征并灵活运用。
7．C
【分析】把48名同学平均分成若干行，那么行数和每行的人数相乘的积是48，根据找因数的方法，可以一对一的找，有多少个因数就有多少种排法，再结合题目进行分析即可。
【详解】由分析可得：
48＝1×48，即每行1人，排48行，不符合题意；或者每行48人，排1行，不符合题意。
48＝2×24，即每行2人，排24行；或每行24人，排2行；
48＝3×16，即每行3人，排16行；或每行16人，排3行；
48＝4×12，即每行4人，排12行；或每行12人，排4行；
48＝6×8，即每行6人，排8行；或每排8人，排6行。
所以共8种排法。
故答案为：C
【点睛】本题考查了找一个数因数的方法，解答此题的关键是把48分解因数，再对分解出来的因数结合题目进行分析，看是否需要排除。
8．A
【分析】根据题意，堆成梯形状的一堆圆木，下层12根，上层7根，每相邻两层差一根，共有（12－7＋1）层，即是梯形的高；
然后根据梯形的面积＝（上底＋下底）×高÷2，代入数据计算，即可求出这堆圆木的总根数。
【详解】层数：
12－7＋1
＝5＋1
＝6（层）
（7＋12）×6÷2
＝19×6÷2
＝57（根）
这堆圆木共有57根。
故答案为：A
【点睛】利用梯形的面积公式求出堆成梯形状的圆木总根数。
9．2
【分析】根据梯形的面积＝（上底＋下底）×高÷2可知：梯形的上底＝面积×2÷高－下底，据此代入数据列式计算即可。
【详解】22.5×2÷5－7
＝45÷5－7
＝9－7
＝2（分米）
【点睛】掌握梯形的面积公式是解答本题的关键。
10． 轴对称 6
【分析】如果一个图形沿着一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．折痕所在的直线叫做对称轴，据此解答。
【详解】是一个轴对称图形，它有6条对称轴。
【点睛】解答此题的关键是理解轴对称图形的意义即可确定对称轴的条数。
11． 25 22
【分析】（1）根据题意，求可以做多少套，也就是求50里面有几个2，根据整数除法的意义，用除法计算；
（2）根据题意，也就是求50里面有几个2.2，也用除法计算，但是50不能被2.2整除，因为剩下的布不足2.2米，就不能再做一套衣服，所以计算结果要用去尾法取值。
【详解】（1）50÷2＝25（套）
做一套校服用布2米，可以做25套；
（2）50÷2.2＝22（套）……1.6（米）
根据去尾法，1.6米＜2.2米，不能再做一套衣服，所以舍去；
每套校服用布2.2米，这些布可以做22套。
【点睛】解决此题的关键是：理解去尾法的意义，即只要是剩下的布不足2.2米，就不能再做一套衣服，都要舍去。
12． 右 6
【分析】由两个图形的位置可知，图形2在图形1的右边，数平移几格时，首先要选中一个关键点，这个点必须是图形1和图形2的同一点，这个点平移了几格，此图形就平移了几格。
【详解】由分析可得：
图形1向右平移，以图形1上半部三角形顶点为观察点，该点向右平移了6格，
综上所述：图形1向右平移6格得到图形2。
【点睛】本题主要考查了平移图形的特点，要能通过确定关键点准确数出图形平移的格子数。
13． 18 14
【分析】根据偶数的性质，相邻的偶数之间相差是2，三个连续的偶数和是48，用48÷3算出中间的偶数，即48÷3＝16，最大的偶数＝中间的偶数＋2，最小的偶数＝中间的偶数－2，即可解答。
【详解】48÷3＝16
16＋2＝18
16－2＝14
【点睛】本题主要考查偶数的性质，关键是三个偶数和除以3求出中间的偶数，以此解答问题。
14．19、41、53、89
【分析】先找出所有两位数中是7的倍数的数，再交换个位上的数字与十位上的数字，找出质数即可。
一个数，如果只有1和它本身两个因数，那么这样的数叫做质数。
【详解】两位数中是7的倍数有：14、21、28、35、42、49、56、63、70、77、84、91、98；
交换个位上的数字与十位上的数字后是质数的有：19、41、53、89。
所以，这样的质数有19、41、53、89。
【点睛】本题考查质数的意义及应用。
15．46.4
【分析】平行四边形的高＝底＋2.2，根据平行四边形的面积＝底×高，代入数据计算即可。
【详解】5.8×（5.8＋2.2）
＝5.8×8
＝46.4（平方厘米）
答：它的面积是46.4平方厘米。
【点睛】掌握平行四边形的面积计算公式，认真计算即可。
16．12.6
【分析】用3千克梨和3千克苹果的钱数减去买了同样的1千克梨和3千克苹果的钱数，即可求出2千克梨的钱数，再除以2，能求出平均每千克梨的钱数，用45.3元减去1千克梨的钱数后再除以3，即可求出平均每千克苹果的钱数。
【详解】由分析可得：
平均每千克梨的钱数：
（60.3－45.3）÷2
＝15÷2
＝7.5（元）
（45.3－7.5）÷3
＝37.8÷3
＝12.6（元）
综上所述：小明买了3千克梨和3千克苹果，共付了60.3元，小芳买了同样的1千克梨和3千克苹果，共付了45.3元，平均每千克苹果12.6元。
【点睛】本题主要考查小数的四则混合运算的计算以及应用，理解题意，找出数量关系，列式计算即可。
17．×
【分析】如果一个图形沿一条直线折叠后，直线两旁的部分能够完全重合，那么这个图形就是轴对称图形，据此对给出的安全标记图形进行判断即可。
【详解】根据轴对称图形的概念可知，这个安全标记不是轴对称图形。
故答案为：×
【点睛】掌握轴对称图形的概念并能据此判断轴对称图形是解答本题的关键。
18．√
【分析】因为在直角三角形中斜边最长，所以高10厘米对应的底边是9厘米。据此根据平行四边形的面积公式计算即可。
【详解】9×10＝90（平方厘米）
这个平行四边形的面积是90平方厘米。
故答案为：√。
【点睛】此题考查了平行四边形的面积计算，找出高对应的底是解题关键。
19．×
【分析】根据一个不等于0的数除以小于1的数，则商大于被除数，一个不等于0的数除以大于1的数，则商小于被除数，题目中只说了是小数，这个小数有可能是大于1的，也可能是小于1的，所以，小数除以小数，商不一定大于被除数。
【详解】由分析可知：
假设两个小数分别是4.5和1.5
即4.5÷1.5＝3
3＜4.5
故答案为：×
【点睛】此题考查的是除法意义，解题时注意商与除数、被除数之间的关系。
20．√
【分析】能被2整除的数叫做偶数；不能被2整除的数叫做奇数；奇数＋奇数＝偶数；偶数＋偶数＝偶数；偶数＋奇数＝奇数；5个连续自然数，如果是3个奇数2个偶数时，和是奇数；如果是2个奇数3个偶数时，和是偶数，举例解答。
【详解】如：0＋1＋2＋3＋4
＝1＋2＋3＋4
＝3＋3＋4
＝6＋4
＝10
10是偶数；
1＋2＋3＋4＋5
＝3＋3＋4＋5
＝6＋4＋5
＝10＋5
＝15
15是奇数，
五个连续自然数的和不是奇数就是偶数。
原题干说法正确。
故答案为：√
【点睛】根据奇数、偶数的意义以及奇偶运算性质进行解答。
21．1.05；3.85；1.54
【分析】小数除法法则：先移动除数的小数点，使它变成整数。除数的小数点向右移动几位，被除数的小数点也向右移动相同的位数（位数不够的补“0”），然后按照除数是整数的除法进行计算。根据商×除数＝被除数进行验算；保留两位小数，计算到小数点后第三位即可；
【详解】16.8÷16＝1.05 ★21.56÷5.6＝3.85 5.4÷3.5≈1.54
验算：
22．43；16.66；46.44
【分析】利用乘法分配律计算；利用乘法分配律计算；先算除法，再算乘法。
【详解】4.3×1.82＋8.18×4.3
＝4.3×（1.82＋8.18）
＝4.3×10
＝43；
0.17×99－0.17
＝0.17×（99－1）
＝0.17×98
＝16.66；
10.8×（3.87÷0.9）
＝10.8×4.3
＝46.44
23．；
【分析】三角形的面积＝底×高÷2，代入数据计算即可；
梯形的面积＝（上底＋下底）×高÷2，代入数据计算即可；
【详解】9.6×7.2÷2
＝69.12÷2
＝34.56（cm2）
（12＋18）×5.4÷2
＝30×5.4÷2
＝162÷2
＝81（cm2）
24．见详解
【分析】（1）根据平移图形的特征，把小鱼的5个顶点分别向上平移3格，再向右平移1格，再首尾依次连结各点，即可得到小鱼向上平移3格，再向右平移1格后图形；
（2）根据轴对称图形的特征，对称点到对称轴的距离相等，据此画出正方形的对角线作为对称轴画图即可；
（3）根据轴对称图形的特征，对称点到对称轴的距离相等，对称点的连线垂直于对称轴，在对称轴的右边画出图形小船的关键对称点，依次连结即可。
【详解】作图如下：
【点睛】此题是考查作轴对称图形、作平移的图形，平移后的图形关键是把对应点的位置画正确。
25．300平方米；450平方米
【分析】根据梯形面积公式：梯形面积＝（上底＋下底）×高÷2，代入数据求出梯形菜地的面积，再根据三角形面积公式：三角形面积＝底×高÷2，代入数据求出黄瓜种的面积，最后用梯形菜地面积减去种黄瓜的面积可求出辣椒的面积。
【详解】由分析可得：
（30＋45）×20÷2
＝75×20÷2
＝1500÷2
＝750（平方米）
20×30÷2
＝600÷2
＝300（平方米）
750－300＝450（平方米）
答：黄瓜种了300平方米，辣椒种了450平方米。
【点睛】本题考查了梯形面积公式和三角形面积公式，解题的关键是熟背公式，并且会结合题目灵活运用。
26．154.8元
【分析】根据总价÷数量＝单价，即用103.2除以4即可得到1件T恤的价格，再根据单价×数量＝总价，用1件T恤的价格乘6即可求解。
【详解】103.2÷4＝25.8（元）
25.8×6＝154.8（元）
答：6件T恤154.8元。
【点睛】本题考查小数乘除法，明确单价、数量和总价之间的关系是解题的关键。
27．不能；能；理由见详解
【分析】一个数各位上的数的和是3的倍数，这个数就是3的倍数。据此判断65是不是3的倍数，若65是3的倍数，则能正好装完，否则不能正好装完；个位上是0或5的数都是5的倍数。据此判断65是不是5的倍数，若65是5的倍数，则能正好装完，否则不能正好装完。
【详解】因为6＋5＝11，11不是3的倍数，即65不是3的倍数，所以如果每3个装一袋，不能正好装完。
因为65的个位上是5，即65是5的倍数，所以如果每5个装一袋，能正好装完。
【点睛】熟练掌握3和5的倍数特征是解决此题的关键。
28．1024块
【分析】整数中，是2的倍数的数叫偶数，不是2的倍数的数叫奇数。
除了1和它本身以外不再有其他因数，这样的数叫质数；除了1和它本身以外还有其他因数，这样的数叫合数。
据此确定各数位上的数，写出这个四位数即可。
【详解】1既不是质数也不是合数，所以A是1；最小的偶数是0，所以B是0；最小的质数是2，所以C是2；最小的合数是4，所以D是4，因此表示的四位数是1024。
答：一共安装了1024块光伏玻璃。
【点睛】关键是理解奇数、偶数、质数、合数的分类标准。
29．111个
【分析】一个蛋糕需要面粉0.35千克，求39千克面粉最多可以做蛋糕的个数，就是求39千克里面有多少个0.35千克，用39除以0.35即可求解。
【详解】39÷0.35≈111（个）
答：最多能做111个这样的蛋糕。
【点睛】解决本题根据除法的包含意义列式求解，注意结果根据去尾法保留整数。
30．1800千克
【分析】平行四边形的面积＝底×高，代入数据求出平行四边形菜地的面积，再乘每平方米收青菜的质量即可。
【详解】20×12×7.5
＝240×7.5
＝1800（千克）
答：这块菜地共收青菜1800千克。
【点睛】本题主要考查平行四边形面积公式的应用，牢记公式是解题的关键。