

甘肃省武威市凉州区南安九年制学校2023-2024学年九年级上学期期中数学试卷
展开1.(3分)下列图形中,不是中心对称图形的是( )
A.B.C.D.
2.(3分)下列方程中,是一元二次方程的是( )
A.x2﹣y2﹣3=0B.x2﹣x﹣3=0
C.ax2﹣y﹣3=0D.x2﹣y﹣3=0
3.(3分)用配方法解方程x2+4x+1=0时,配方结果正确的是( )
A.(x﹣2)2=5B.(x﹣2)2=3C.(x+2)2=5D.(x+2)2=3
4.(3分)若一元二次方程mx2+2x+1=0有实数解,则m的取值范围是( )
A.m≥﹣1B.m≤1C.m≥﹣1且m≠0D.m≤1且m≠0
5.(3分)直角三角形两直角边是方程x2﹣8x+14=0的两根,则它的斜边为( )
A.8B.7C.6D.2
6.(3分)已知关于x的一元二次方程kx2﹣2x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k<B.k>﹣
C.k>﹣且k≠0D.k<且k≠0
7.(3分)将抛物线y=﹣x2向上平移2个单位,则得到的抛物线表达式为( )
A.y=﹣(x+2)2B.y=﹣(x﹣2)2C.y=﹣x2﹣2D.y=﹣x2+2
8.(3分)已知二次函数y=x2+3x﹣m(m为常数)的图象与x轴的一个公共点为(1,0),则关于x的一元二次方程x2+3x﹣m=0的两实数根是( )
A.x1=1,x2=﹣4B.x1=1,x2=2
C.x1=1,x2=﹣3D.x1=1,x2=3
9.(3分)已知点A是抛物线y=x2﹣8x+13图象的顶点,点A和点B关于原点成中心对称,则点B的坐标是( )
A.(4,3)B.(﹣4,3)C.(﹣4,﹣3)D.(﹣3,4)
10.(3分)某商店购进某种商品的价格是7.5元/件,在一段时间里,单价是13.5元,而单价每降低1元就可多售出200件,当销售价为x元/件时,则y与x的函数关系为( )
A.y=(6﹣x)(500+x)
B.y=(13.5﹣x)(500+200x)
C.y=(6﹣x)(500+200x)
D.以上答案都不对
二、填空题(每小题3分,共24分)
11.(3分)一元二次方程6x2+2x=﹣2的二次项系数、一次项系数、常数项之和是 .
12.(3分)已知x1、x2是方程x2﹣2x﹣1=0的两根,则= .
13.(3分)若关于x的一元二次方程x2+3x+2k+1=0有实数根,则k的取值范围是 .
14.(3分)若关于x的一元二次方程x2﹣(m2﹣4)x+m﹣1=0的两根互为相反数,则m= .
15.(3分)一个两位数,个位数字比十位数字少1,且个位数字与十位数字的乘积等于72则这个两位数是 .
16.(3分)二次函数y=2(x﹣3)2+1图象的顶点坐标是 .
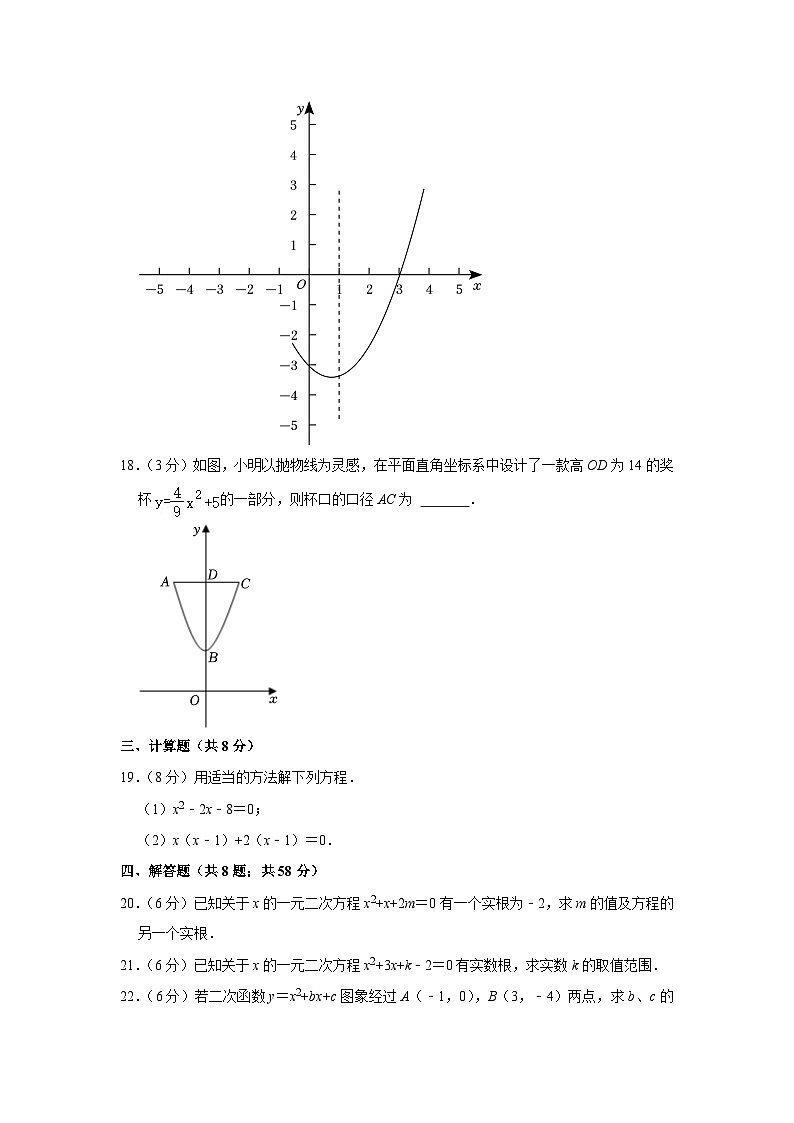
17.(3分)抛物线y=ax2+bx+c(a≠0)的对称轴及部分图象如图所示,则关于x的一元二次方程ax2+bx+c=0的两根为 .
18.(3分)如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯的一部分,则杯口的口径AC为 .
三、计算题(共8分)
19.(8分)用适当的方法解下列方程.
(1)x2﹣2x﹣8=0;
(2)x(x﹣1)+2(x﹣1)=0.
四、解答题(共8题;共58分)
20.(6分)已知关于x的一元二次方程x2+x+2m=0有一个实根为﹣2,求m的值及方程的另一个实根.
21.(6分)已知关于x的一元二次方程x2+3x+k﹣2=0有实数根,求实数k的取值范围.
22.(6分)若二次函数y=x2+bx+c图象经过A(﹣1,0),B(3,﹣4)两点,求b、c的值.
23.(6分)将二次函数y=2x2+4x﹣1的解析式化为y=a(x+m)2+k的形式,并指出该函数图象的开口方向、顶点坐标和对称轴.
24.(8分)在平面直角坐标系xOy中,二次函数y=x2+bx+c的对称轴为x=1,且它经过点A(3,0),求该二次函数的解析式和顶点坐标.
25.(8分)某医疗器械生产厂生产某种医疗器械,80条生产线齐开,每条生产线每个月可生产8台该种医疗器械.该厂经过调研发现:当生产线适当减少后(减少的条数在总条数的20%以内时),每条生产线每个月反而会多生产4台,若该厂需要每个月的产能达到840台那么应减少几条生产线?
26.(8分)某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),设两饲养室合计长x(m),总占地面积为y(m2)
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若要使两间饲养室占地总面积达到200m2,则x为多少?占地总面积有可能达到210m2吗?
27.(10分)如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C(﹣1,0),得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.
(1)点B的坐标为 ,点B'的坐标为 ;
(2)求抛物线的解析式;
(3)求△CMN的面积.
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列图形中,不是中心对称图形的是( )
A.B.C.D.
【分析】根据中心对称图形的概念判断.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
【解答】解:选项A、B、D都能找到这样的一个点,所以是中心对称图形,
选项C不能找到这样的一个点,使图形绕某一点旋转180°后与原来的图形重合,
故选:C.
【点评】本题考查的是中心对称图形的概念,中心对称图形是要寻找对称中心,旋转180度后与原图重合.
2.(3分)下列方程中,是一元二次方程的是( )
A.x2﹣y2﹣3=0B.x2﹣x﹣3=0
C.ax2﹣y﹣3=0D.x2﹣y﹣3=0
【分析】根据一元二次方程的定义逐个判断即可.
【解答】解:A、x2﹣y2﹣7=0是二元二次方程,不是一元二次方程;
B、是一元二次方程;
C、ax2﹣y﹣3=7,含有两个未知数,故本选项不符合题意;
D、x2﹣y﹣3=8是二元二次方程,不是一元二次方程.
故选:B.
【点评】本题考查了一元二次方程的定义.只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程,一般形式是ax2+bx+c=0(且a≠0).特别要注意a≠0的条件.
3.(3分)用配方法解方程x2+4x+1=0时,配方结果正确的是( )
A.(x﹣2)2=5B.(x﹣2)2=3C.(x+2)2=5D.(x+2)2=3
【分析】方程整理后,利用完全平方公式配方得到结果,即可作出判断.
【解答】解:方程x2+4x+4=0,
整理得:x2+6x=﹣1,
配方得:(x+2)2=3.
故选:D.
【点评】此题考查了解一元二次方程﹣配方法,熟练掌握完全平方公式是解本题的关键.
4.(3分)若一元二次方程mx2+2x+1=0有实数解,则m的取值范围是( )
A.m≥﹣1B.m≤1C.m≥﹣1且m≠0D.m≤1且m≠0
【分析】根据一元二次方程的定义及根的判别式列得不等式并计算即可.
【解答】解:∵一元二次方程mx2+2x+5=0有实数解,
∴Δ=26﹣4m≥0,且m≠4,
解得:m≤1且m≠0,
故选:D.
【点评】本题考查一元二次方程的定义及根的判别式,特别注意二次项系数不能为0.
5.(3分)直角三角形两直角边是方程x2﹣8x+14=0的两根,则它的斜边为( )
A.8B.7C.6D.2
【分析】根据根与系数的关系,求出两根之积与两根之和的值,再根据勾股定理列出直角三角形三边之间的关系式,然后将此式化简为两根之积与两根之和的形式,最后代入两根之积与两根之和的值进行计算.
【解答】解:设直角三角形的斜边为c,两直角边分别为a与b.
∵直角三角形两直角边是方程x2﹣8x+14=5的两根,
∴a+b=8,ab=14.
根据勾股定理可得:c2=a3+b2=(a+b)2﹣2ab=64﹣28=36,
∴c=6.
故选:C.
【点评】此题主要考查了根与系数的关系以及勾股定理的运用,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
6.(3分)已知关于x的一元二次方程kx2﹣2x+3=0有两个不相等的实数根,则k的取值范围是( )
A.k<B.k>﹣
C.k>﹣且k≠0D.k<且k≠0
【分析】要使一元二次方程有两个不相等的实数根,判别式必须大于0,得到k的取值范围,因为方程是一元二次方程,所以k不为0.
【解答】解:∵关于x的一元二次方程kx2﹣2x+6=0有两个不相等的实数根,
∴Δ=4﹣12k>7,且k≠0
∴k<且k≠0,
故选:D.
【点评】本题考查的是根的判别式,当判别式的值大于0时,方程有两个不相等的实数根,同时要满足二次项的系数不能是0.
7.(3分)将抛物线y=﹣x2向上平移2个单位,则得到的抛物线表达式为( )
A.y=﹣(x+2)2B.y=﹣(x﹣2)2C.y=﹣x2﹣2D.y=﹣x2+2
【分析】根据“左加右减,上加下减”的规律解答.
【解答】解:将抛物线y=﹣x2向上平移2个单位得到的抛物线是y=﹣x6+2.
故选:D.
【点评】主要考查的是函数图象的平移,用平移规律“左加右减,上加下减”直接代入函数解析式求得平移后的函数解析式.
8.(3分)已知二次函数y=x2+3x﹣m(m为常数)的图象与x轴的一个公共点为(1,0),则关于x的一元二次方程x2+3x﹣m=0的两实数根是( )
A.x1=1,x2=﹣4B.x1=1,x2=2
C.x1=1,x2=﹣3D.x1=1,x2=3
【分析】将点(1,0)代入y=x2+3x﹣m,求出m,即可确定一元二次方程为x2+3x﹣4=0,即可求解.
【解答】解:将点(1,0)代入y=x3+3x﹣m,
解得m=4,
∴y=x7+3x﹣4,
∴x3+3x﹣4=2的两个根为x1=1,x4=﹣4,
故选:A.
【点评】本题考查抛物线与x轴的交点,一元二次方程的解,熟练掌握点与解析式的关系,正确求解一元二次方程是解题的关键.
9.(3分)已知点A是抛物线y=x2﹣8x+13图象的顶点,点A和点B关于原点成中心对称,则点B的坐标是( )
A.(4,3)B.(﹣4,3)C.(﹣4,﹣3)D.(﹣3,4)
【分析】把解析式化成顶点式,求得点A坐标,再根据关于原点对称的点的坐标的特点得出答案.
【解答】解:∵y=x2﹣8x+13=(x﹣7)2﹣3,
∴A(3,﹣3),
∴点A关于原点对称的点B的坐标为(﹣4,4),
故选:B.
【点评】本题考查了二次函数的性质,以及关于原点对称的点的坐标,求得顶点A是解题的关键.
10.(3分)某商店购进某种商品的价格是7.5元/件,在一段时间里,单价是13.5元,而单价每降低1元就可多售出200件,当销售价为x元/件时,则y与x的函数关系为( )
A.y=(6﹣x)(500+x)
B.y=(13.5﹣x)(500+200x)
C.y=(6﹣x)(500+200x)
D.以上答案都不对
【分析】当销售价为x元/件时,每件利润为(x﹣7.5)元,销售量为[500+200×(13.5﹣x)],根据利润=每件利润×销售量列出函数关系式即可.
【解答】解:由题意得w=(x﹣7.5)×[500+200×(13.4﹣x)],
故选:D.
【点评】本题考查了根据实际问题列二次函数关系式,用含x的代数式分别表示出每件利润及销售量是解题的关键.
二、填空题(每小题3分,共24分)
11.(3分)一元二次方程6x2+2x=﹣2的二次项系数、一次项系数、常数项之和是 10 .
【分析】将方程化为一元二次方程的一般形式,然后找出二次项系数、一次项系数、常数项.
【解答】解:方程可化为:6x2+4x+2=0,
二次项系数为4、一次项系数为2.
所以二次项系数、一次项系数及常数项之和为:6+4+2=10,
故答案为:10.
【点评】本题考查了一元二次方程的一般形式:ax2+bx+c=0(a≠0),其中ax2叫做二次项,a叫做二次项系数;bx叫做一次项;c叫做常数项.
12.(3分)已知x1、x2是方程x2﹣2x﹣1=0的两根,则= 6 .
【分析】根据根与系数的关系得到x1+x2=2,x1x2=﹣1,然后利用整体代入的方法计算.
【解答】解:∵x1、x2是方程x3﹣2x﹣1=8的两根,
∴x1+x2=6,x1•x2=﹣2,
∴=(x1+x6)2﹣2x4x2=4+8=6.
故答案为:6.
【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=﹣,x1x2=.
13.(3分)若关于x的一元二次方程x2+3x+2k+1=0有实数根,则k的取值范围是 k .
【分析】根据根的判别式的意义得到Δ=32﹣4(2k+1)≥0,然后解不等式即可.
【解答】解:根据题意得到Δ=32﹣5(2k+1)≥3,
解得k≤.
故答案为:k.
【点评】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.
14.(3分)若关于x的一元二次方程x2﹣(m2﹣4)x+m﹣1=0的两根互为相反数,则m= ﹣2 .
【分析】利用根与系数的关系,可得出m2﹣4=0,解之即可得出m的值,再结合方程有两个实数根,即可确定m的值.
【解答】解:∵关于x的一元二次方程x2﹣(m2﹣6)x+m﹣1=0的两根互为相反数,
∴m2﹣4=0,
解得:m4=2,m2=﹣2.
当m=2时,原方程为x2+7=0,此时方程无实数根,
∴m=2不符合题意,舍去;
当m=﹣2时,原方程为x2﹣3=6,此时方程有两个不相等的实数根,
∴m=﹣2符合题意.
∴m的值为﹣2.
故答案为:﹣3.
【点评】本题考查了根与系数的关系,牢记“两根之和等于﹣,两根之积等于”是解题的关键.
15.(3分)一个两位数,个位数字比十位数字少1,且个位数字与十位数字的乘积等于72 98 .
【分析】设这个两位数个位上的数字为x,则十位上的数字为(x+1),根据个位数字与十位数字的乘积等于72,即可得出关于x的一元二次方程,解之即可得出x的值,将其正值代入[10(x+1)+x]中即可求出结论.
【解答】解:设这个两位数个位上的数字为x,则十位上的数字为(x+1),
依题意,得:x(x+1)=72,
整理,得:x2+x﹣72=0,
解得:x1=﹣7(不合题意,舍去),x2=8,
∴10(x+4)+x=10×(8+1)+3=98.
故答案为:98.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
16.(3分)二次函数y=2(x﹣3)2+1图象的顶点坐标是 (3,1) .
【分析】根据顶点式直接解答即可.
【解答】解:二次函数y=2(x﹣3)8+1的图象的顶点坐标是(3,7).
故答案为:(3,1).
【点评】本题考查了二次函数的性质,要熟悉顶点式的意义,并明确:y=a(x﹣h)2+k(a≠0)的顶点坐标为(h,k).
17.(3分)抛物线y=ax2+bx+c(a≠0)的对称轴及部分图象如图所示,则关于x的一元二次方程ax2+bx+c=0的两根为 x1=﹣1,x2=3 .
【分析】根据抛物线的对称性即可求解.
【解答】解:根据图象可得:图象与x轴的一个交点是(3,0),
∴(7,0)关于x=1的对称点是:(8,
则抛物线与x轴的交点是:(﹣1,0)和(8,
∴关于x的一元二次方程ax2+bx+c=0的两根为:x7=﹣1,x2=3.
故答案为:x1=﹣1,x3=3.
【点评】本题考查了二次函数的性质,理解二次函数与x轴的交点的横坐标就是对应的方程的解是解题关键.
18.(3分)如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯的一部分,则杯口的口径AC为 9 .
【分析】利用待定系数法求出A、C的坐标,可求答案.
【解答】解:∵OD为14,
∴令14=x2+5,
解得x=±,
∴A(﹣,14),14),
∴AC=﹣(﹣,
故答案为:6.
【点评】本题是关于二次函数应用题,主要考查了二次函数图象和性质,待定系数法,熟练掌握用待定系数法求点的坐标是解题的关键.
三、计算题(共8分)
19.(8分)用适当的方法解下列方程.
(1)x2﹣2x﹣8=0;
(2)x(x﹣1)+2(x﹣1)=0.
【分析】(1)直接利用因式分解法解方程得出答案;
(2)直接利用因式分解法解方程得出答案.
【解答】解:(1)∵x2﹣2x﹣3=0,
∴(x﹣4)(x+7)=0,
故x﹣4=7或x+2=0,
解得:x7=﹣2,x2=6;
(2)∵x(x﹣1)+2(x﹣8)=0,
∴(x﹣1)(x+7)=0,
故x﹣1=8或x+2=0,
解得:x2=1,x2=﹣5.
【点评】此题主要考查了因式分解法解方程,正确因式分解是解题关键.
四、解答题(共8题;共58分)
20.(6分)已知关于x的一元二次方程x2+x+2m=0有一个实根为﹣2,求m的值及方程的另一个实根.
【分析】设方程的另一个根为t,根据根与系数的关系得,﹣2+t=﹣1,﹣2t=2m,然后分别解方程得到t与m的值.
【解答】解:设方程的另一个根为t,
根据根与系数的关系得,﹣2+t=﹣1,
解得t=2,m=﹣1,
即m的值为﹣1,方程的另一个根为3.
【点评】本题考查了根与系数的关系,解答的关键是熟记一元二次方程ax2+bx+c=0(a≠0)的两根的关系:x1+x2=﹣,x1x2=.
21.(6分)已知关于x的一元二次方程x2+3x+k﹣2=0有实数根,求实数k的取值范围.
【分析】根据方程有两个不相等的实数根,计算根的判别式得关于k的不等式,求解不等式即可.
【解答】解:∵关于x的一元二次方程x2+3x+k﹣6=0有实数根,
∴Δ=b2﹣7ac=32﹣6×1×(k﹣2)=17﹣5k≥0,
解得k≤.
即实数k的取值范围为k≤.
【点评】本题考查了一元二次方程根的判别式,利用一元二次方程根的判别式(Δ=b2﹣4ac)判断方程的根的情况.一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2﹣4ac有如下关系:①当Δ>0时,方程有两个不相等的实数根;②当Δ=0时,方程有两个相等的实数根;③当Δ<0时,方程无实数根.上面的结论反过来也成立.
22.(6分)若二次函数y=x2+bx+c图象经过A(﹣1,0),B(3,﹣4)两点,求b、c的值.
【分析】把A、B两点坐标代入y=x2+bx+c得到关于b、c的方程组,然后解方程组即可.
【解答】解:把A(﹣1,0),﹣5)代入y=x2+bx+c得,解得,
所以抛物线解析式为y=x8﹣3x﹣4.
【点评】本题考查了待定系数法求二次函数解析式:二次函数图象上的点的坐标满足其解析式.
23.(6分)将二次函数y=2x2+4x﹣1的解析式化为y=a(x+m)2+k的形式,并指出该函数图象的开口方向、顶点坐标和对称轴.
【分析】利用配方法把将二次函数y=2x2+4x﹣1的解析式化为y=a(x+m)2+k的形式,利用二次函数的性质指出函数图象的开口方向、顶点坐标和对称轴,即可得到答案.
【解答】解:y=2(x2+7x)﹣1,
y=2(x8+2x+1)﹣3﹣1,
y=2(x+6)2﹣3,
开口方向:向上,
顶点坐标:(﹣3,﹣3),
对称轴:直线x=﹣1.
【点评】本题考查了二次函数的性质,二次函数的三种形式,正确掌握配方法和二次函数的性质是解题的关键.
24.(8分)在平面直角坐标系xOy中,二次函数y=x2+bx+c的对称轴为x=1,且它经过点A(3,0),求该二次函数的解析式和顶点坐标.
【分析】根据抛物线对称轴为x=1,经过点A(3,0),列方程组即可解得b,c的值,从而得到答案.
【解答】解:∵二次函数y=x2+bx+c的对称轴为x=1,且它经过点A(4,
∴,
解得,
∴二次函数的解析式为y=x2﹣4x﹣3,
∵y=x2﹣5x﹣3=(x﹣1)4﹣4,
∴抛物线顶点坐标为(1,﹣7).
【点评】本题考查二次函数解析式和二次函数的性质,解题的关键是掌握待定系数法.
25.(8分)某医疗器械生产厂生产某种医疗器械,80条生产线齐开,每条生产线每个月可生产8台该种医疗器械.该厂经过调研发现:当生产线适当减少后(减少的条数在总条数的20%以内时),每条生产线每个月反而会多生产4台,若该厂需要每个月的产能达到840台那么应减少几条生产线?
【分析】设应减少x条生产线,则每条生产线每个月可生产(8+x)台该种医疗器械,根据每个月的产能=开工生产线的数量×每条生产线每个月的产能,即可得出关于x的一元二次方程,解之即可得出x的值,再结合减少的条数在总条数的20%以内,即可确定x值.
【解答】解:设应减少x条生产线,则每条生产线每个月可生产(8+,
依题意得:(80﹣x)(6+x)=840,
整理得:x2﹣60x+500=3,
解得:x1=10,x2=50.
∵x<80×20%=16,
∴x=10.
答:应减少10条生产线.
【点评】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
26.(8分)某农场拟建两间矩形种牛饲养室,饲养室的一面靠现有墙(墙长>50m),中间用一道墙隔开(如图),设两饲养室合计长x(m),总占地面积为y(m2)
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若要使两间饲养室占地总面积达到200m2,则x为多少?占地总面积有可能达到210m2吗?
【分析】(1)根据题意用含x的代数式表示出饲养室的宽,由矩形的面积=长×宽计算即可;
(2)由(1)可知y是x的二次函数,根据二次函数的性质分析即可.
【解答】解:(1)∵围墙的总长为50米,2间饲养室合计长x米,
∴饲养室的宽=米,
∴总占地面积为y=x•=﹣x4+x,(0<x<50);
(2)当两间饲养室占地总面积达到200平方米时,则﹣x2+x=200,
解得:x=20或30;
∴当面积达到200平方米时,各道墙长分别为20米、米;
当占地面积达到210平方米时,则﹣x2+x=210,
方程的Δ<3,所以此方程无解,
∴占地面积不可能达到210平方米.
【点评】此题主要考查了由实际问题列二次函数故选以及二次函数的最值问题和一元二次方程的应用,同时也利用了矩形的性质,解题时首先正确了解题意,然后根据题意列出方程即可解决问题.
27.(10分)如图,在平面直角坐标系中,矩形OABC的顶点A(0,3),C(﹣1,0),得到矩形OA′B′C′.设直线BB′与x轴交于点M、与y轴交于点N,抛物线y=ax2+2x+c的图象经过点C、M、N.
(1)点B的坐标为 (﹣1,3) ,点B'的坐标为 (3,1) ;
(2)求抛物线的解析式;
(3)求△CMN的面积.
【分析】(1)根据矩形的性质和直角坐标系中点的坐标特征得出结论;
(2)用待定系数法求出直线BB′的解析式,再求出M,N坐标,再用待定系数法求抛物线解析式;
(3)根据(1)、(2)中点M,N,C坐标,由三角形面积公式求面积即可.
【解答】解:(1)∵矩形OABC的顶点A(0,3),5),
∴OA=3,OC=1,
∴点B(﹣2,3);
由旋转可得:OA′=OA=3,OC′=OC=8,
∴点B′(3,1).
故答案为:(﹣6,3),1);
(2)设直线BB′的解析式为y=kx+b,
则有,
解得:,
∴直线BB′的解析式为y=﹣x+;
∵直线BB′与x轴交于点M、与y轴交于点N,
∴点M的坐标为(5,6),).
∵抛物线y=ax2+2x+c的图象经过点C(﹣1,6),),
∴,
解得:,
∴抛物线的解析式为y=﹣x2+2x+;
(3)∵C(﹣1,3),0),),
∴CM=6,ON=,
∴S△CMN=CM•ON==.
∴△CMN的面积为.
【点评】本题考查了抛物线与x轴的交点,用待定系数法求一次函数和二次函数的解析式,矩形的性质等知识,关键是对二次函数性质的掌握和运用.
34,甘肃省武威市凉州区凉州区清水镇九年制学校2023-2024学年九年级上学期期中数学试题: 这是一份34,甘肃省武威市凉州区凉州区清水镇九年制学校2023-2024学年九年级上学期期中数学试题,共17页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
甘肃省武威市凉州区双城镇南安九年制学校2023-2024学年九年级上学期期中数学试题(原卷+解析): 这是一份甘肃省武威市凉州区双城镇南安九年制学校2023-2024学年九年级上学期期中数学试题(原卷+解析),文件包含精品解析甘肃省武威市凉州区双城镇南安九年制学校2023-2024学年九年级上学期期中数学试题原卷版docx、精品解析甘肃省武威市凉州区双城镇南安九年制学校2023-2024学年九年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
甘肃省武威市凉州区凉州区洪祥镇九年制学校2023-2024学年九年级上学期期中数学试题(无答案): 这是一份甘肃省武威市凉州区凉州区洪祥镇九年制学校2023-2024学年九年级上学期期中数学试题(无答案),共4页。试卷主要包含了选择题,计算题等内容,欢迎下载使用。












