

浙江省宁波市五校2022-2023学年高二上学期期中联考数学试卷(含答案)
展开
这是一份浙江省宁波市五校2022-2023学年高二上学期期中联考数学试卷(含答案),文件包含核心素养人教版小学数学五年级下册27奇偶性课件pptx、核心素养人教版小学数学五年级下册《奇偶性》教案docxdocx、核心素养人教版小学数学五年级下册27奇偶性导学案docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
一、选择题
1、直线的一个方向向量是( )
A.B.C.D.
2、设A是空间一定点,为空间内任一非零向量,满足条件的点M构成的图形是( )
A.圆B.直线C.平面D.线段
3、在平面直角坐标系xOy中,双曲线的渐近线方程为( )
A.B.C.D.
4、圆与圆的公共弦所在直线方程为( )
A.B.
C.D.
5、以双曲线的焦点为顶点,顶点为焦点的椭圆方程是( )
A. B. C. D.
6、如图,在三棱锥中,点P,Q分别是OA,BC的中点,点G是PQ的中点,若记,,,则( )
A.B.
C.D.
7、已知点P在直线上运动,点E是圆上的动点,点F是圆上的动点,则的最大值是( )
A.13B.16C.17D.18
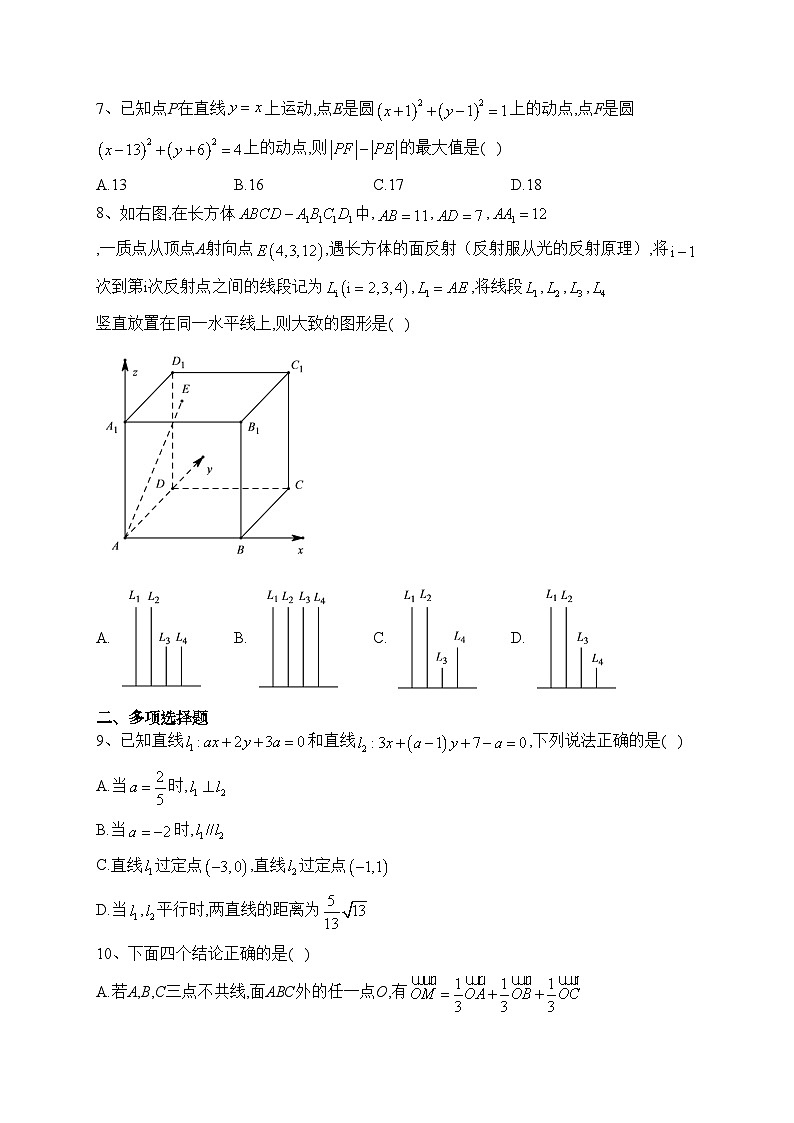
8、如右图,在长方体中,,,,一质点从顶点A射向点,遇长方体的面反射(反射服从光的反射原理),将次到第i次反射点之间的线段记为,,将线段,,,竖直放置在同一水平线上,则大致的图形是( )
A.B.C.D.
二、多项选择题
9、已知直线和直线,下列说法正确的是( )
A.当时,
B.当时,
C.直线过定点,直线过定点
D.当,平行时,两直线的距离为
10、下面四个结论正确的是( )
A.若A,B,C三点不共线,面ABC外的任一点O,有,则M,A,B,C四点共面
B.有两个不同的平面,的法向量分别为,,且,,则
C.已知为平面的一个法向量,为直线l的一个方向向量,若,则l与所成角为
D.已知向量,,若,则为钝角
11、有很多立体图形都体现了数学的对称美,其中半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体因其最早由阿基米德研究发现,故也被称作阿基米德体.如图,将正方体沿交于一顶点的三条棱的中点截去一个三棱锥,共截去八个三棱锥,则关于该半正多面体的下列说法中正确的是( )
A.该半正多面体外接球与原正方体的外接球半径相等
B.与DF所成的角是的棱共有18条
C.DF与平面BCD所成的角
D.若点E为线段BC上的动点,直线DE与直线AF所成角的余弦值的取值范围为
12、已知双曲线与直线交于A,B两点,点P为C上一动点,记直线PA,PB的斜率分别为,,曲线C的左、右焦点分别为,.若,且C的焦点到渐近线的距离为1,则下列说法正确的是( )
A.
B.C的离心率为
C.若,则的面积为2
D.若的面积为,则为钝角三角形
三、填空题
13、在空间直角坐标系中,已知,,则MN的中点P到坐标原点O的距离为____________.
14、经过点,且在x轴上的截距是在y轴上的截距的2倍的直线l的方程是______.
四、双空题
15、已知圆,若圆与圆M内切,则_________;若点P是圆M上一动点,满足“点P到直线的距离等于2”的点,在圆M上有且仅有三个,则______.
16、如图,已知、分别为椭圆的左、右焦点,过的直线与椭圆交于P、Q两点,若,,则_________,椭圆的离心率为________.
五、解答题
17、已知点,及点;
(1)若直线l经过点P且,求直线l的方程;
(2)求的面积.
18、已知向量,,.
(1)求;
(2)求在方向上的投影向量;
(3)若,求m,n的值.
19、如图,在五面体ABCDEF中,四边形ABCD是矩形,,,,平面ABCD.
(1)若点G是AC的中点,求证:平面AED;
(2)求点D到平面AFC的距离.
20、已知点,O为坐标原点,圆.
(1)若直线l过点M,且被圆C截得的弦长为,求直线l的方程;
(2)已知点N在圆C上运动,线段MN的中点为P,设动点P的轨迹为曲线W;若直线上存在点Q,过点Q作曲线W的两条切线QA,QB,切点为A,B,且,求实数m的取值范围.
21、如图,已知矩形ABCD中,,,M为DC的中点,将 沿AM折起,使得平面平面ABCM.
(1)求证:平面平面BDM;
(2)若点E是线段DB上的一动点,且,当二面角 的余弦值为时, 求t的值.
22、椭圆的右焦点是,且经过点;直线l与椭圆交于A,B两点,以AB为直径的圆过原点.
(1)求椭圆方程;
(2)若过原点的直线m与椭圆交于C,D两点,且,求四边形ACBD面积的范围.
参考答案
1、答案:A
解析:一个方向向量是,
故选:A.
2、答案:C
解析:由题意,故点M位于过点A且和垂直的平面内,
故点M构成的图形是经过点A,且以为法向量的平面,
故选:C.
3、答案:B
解析:由双曲线,可得其标准方程为,所以,
则双曲线的渐近线方程为.
故选:B.
4、答案:C
解析:联立,相减可得,
故选:C
5、答案:C
解析:双曲线的焦点坐标为,
顶点坐标为,
由题意得:椭圆的焦点为,
顶点坐标为,
所以椭圆的方程是,
故选:C.
6、答案:A
解析:由在三棱锥中,点P,Q分别是OA,BC的中点,点G是PQ的中点,
如图所示,连接OQ,根据空间向量的线性运算法则,
可得:
.
故选:A.
7、答案:B
解析:设直线:,圆,圆,
易知点关于直线的对称点为,以为圆心,以1为半径的圆即为圆A关于直线l的对称圆.设E点关于直线l的对称点为,则有,
,
如图,连接,
在中,有,当且仅当P,,F三点共线时取得等号,
故求解的最大值问题转换为求最大值问题,
故当直线过圆心和圆心B且,F距离最远且点P恰好为直线与直线l的交点时可取得最大值.
由题意知点和B点坐标分别为:,,两圆半径分别为1和2,
故最大值为:.
故选:B.
8、答案:C
解析:因为,所以延长交于F,过F作FM垂直DC于M.
在矩形中分析反射情况:由于,第二次反射点为在线段AM上,此时,第三次反射点为在线段FM上,此时,第四次反射点为在线段上,由图可知,
选C.
9、答案:AD
解析:对于A,当时,那么直线为,直线为,此时两直线的斜率分别为和,所以有,所以,故A选项正确;
对于B,当时,那么直线为,直线为,此时两直线重合,故B选项错误;
对于C,由直线,整理可得: ,故直线过定点,
直线,整理可得:,故直线过定点,故C选项错误;
对于D,当,平行时,两直线的斜率相等,即,解得:或,当时,两直线重合,舍去;当时,直线为,为,此时两直线的距离,故D选项正确.
故选:AD.
10、答案:AC
解析:对于A:,即,M,A,B,C四点共面,故A正确,
对于B:,,,即与不平行,与不平行,故B错误,
对于C:若,则l与所成角为,故C正确,
对于D:,,
若,则,
若,反向,则,,
,,
当且时,为钝角,故D错误,
故选:AC.
11、答案:CD
解析:设棱长为的半正多面体,它的所有顶点都在同一个正方体的表面上,
将该半正多面体补成正方体,
正方体的棱长为2,可得该半正多面体的外接球与原正方体的外接球的球心重合,
但半径分别为和,故A错误;
与DF成的棱有HF,AG,AF,GH和与面AFHG相对的面上的CI,JN,CJ,IN;
还有DH,BC,CD,BH和与面BCDH相对的面上的AM,NS,MN,AS,共16条,故B错误;
由平面BCDH,可得为DF与平面BCD所成角,由于为等腰直角三角形,
所以,故C正确;
建立如图所示的空间直角坐标系,
则,,,,
,,,,
设,
则,
可解得,则,,共面,即A,C,D,F四点共面,
又,设,所以,
则,,,,,,
,令,则,
因为,所以,
故直线DE与直线AF所成角的余弦值的取值范围为,,故D正确.
故选:CD.
12、答案:ABD
解析:设点,,则且,
两式相减,得,所以,
因为,所以,所以,
所以双曲线的渐近线方程为,
因为焦点到渐近线的距离为1,
所以,可得,又因,所以,
所以双曲线的离心率为,所以A、B正确;
对于C中,不妨设P在右支上,记,则,
因为,所以,解得或(舍去),
所以的面积为,所以C不正确;
对于D中,设,因为,所以,
将代入,可得,
由双曲线的对称性,不妨取P的坐标为,则,
,
因为,
所以为钝角,所以为钝角三角形,所以D正确.
故选:ABD.
13、答案:
解析:由,可得
则
即点P到坐标原点O的距离为
故答案为:.
14、答案:和;
解析:若直线经过原点,则设直线方程为,将代入可得,
若直线不经过原点,设直线方程为,
将代入可得,所以直线方程为,即,
故答案为:和;
15、答案:①.18②.7
解析:由圆,得,
由圆,得,
由已知得,解得;
圆心M到直线的距离为,
又“点P到直线的距离等于2”的点,在圆M上有且仅有三个,
,
.
故答案为:18;7.
16、答案:①.②.
解析:由可得,
所以,
故
设,则,,
在三角形中,,故,
在三角形中,,
故,
故答案为:;.
17、答案:(1);
(2)5.
解析:(1)由题意可得:,
直线l的方程为,即
则直线l的方程为
(2)由题意可得直线MN的方程为:,即,
点P到直线MN的距离为,
,
的面积
的面积为5.
18、答案:(1)
(2)
(3),
解析:(1),,
,
所以
(2)
(3),存在实数,使得,
,故,
解得,,
19、答案:(1)证明见解析
(2)
解析:(1)平面ABCD,,EA,AD,AB两两垂直,
故以A为坐标原点,AD,AB,AE所在直线分别为x,y,z轴建立空间直角坐标系
,,
平面DAE的一个法向量,
故,
又平面AED, 平面AED
(2),,
设面AFC的一个法向量为
,取,则,故
,
所以点D到平面AFC的距离为.
20、答案:(1)或
(2)
解析:(1)由题意,圆,可得圆心,半径,
因为直线l被圆C截得的弦长为,则圆心到直线l的距离为,
当直线l的斜率不存在时,此时直线l的方程为,满足题意;
当直线l的斜率存在时,设直线l的方程为,即,
则,解得,即,
综上可得,所求直线的方程为或.
(2)设点,
因为点,线段MN的中点为P,可得,解得,
又因为N在圆C上,可得,即,
所以点P的轨迹即曲线W的方程为圆,
由,可得,
在直角中,,所以到直线q距离,
解得,即实数m的取值范围为.
21、答案:(1)证明见解析;
(2).
解析:(1)证明:因为在矩形ABCD中,,,M为DC的中点,
所以,
因为,所以,
因为平面平面ABCM,平面平面,平面ABCM,所以平面ADM,
因为平面BDM,所以,平面平面BDM.
(2)取AM中点O,连接DO,
,O为AM的中点,则,
因为平面平面ABCM,平面平面,平面ADM,
所以,平面ABCM,
过点O在平面ABCM内作AM的垂线,交AB于点F,
以O为原点,OA、OF、OD所在直线分别为x、y、z轴建立如下图所示空间直角坐标系,
则、、、,
易知平面ADM的一个法向量为,
因为且,所以,
,.
设平面AME的一个法向量为,则,
即,取,得.
所以,因为,解得.
22、答案:(1)
(2)
解析:(1)焦点F为,则,即,
点在椭圆上,即,
解得或(舍去),则,
所以椭圆的方程为;
(2)当直线AB斜率存在时,设其方程为,,,
联立,可得,
则①,
又②,③
以AB为直径的圆过原点即,
化简可得,
代入②③两式,整理得,
即④,
将④式代入①式,得恒成立,则,
设线段AB中点为M,由,所以,
又,
又由,则C点坐标为,
化简可得,
代入椭圆方程可得,即,
则
,
当直线AB斜率不存在时,AB方程为,直线CD过AB中点,即为x轴,易得,,,
综上,四边形ACBD面积的取值范围为.
相关试卷
这是一份浙江省宁波市九校2022-2023学年高二上学期期末联考数学试题,共26页。试卷主要包含了 直线的倾斜角为, 设,向量,且,则, 已知函数及其导函数满足,则, 若动点满足等内容,欢迎下载使用。
这是一份浙江省宁波市九校2022-2023学年高二上学期期末联考数学试题,共26页。试卷主要包含了 直线的倾斜角为, 设,向量,且,则, 已知函数及其导函数满足,则, 若动点满足等内容,欢迎下载使用。
这是一份浙江省宁波市五校2023-2024学年高二上学期期中联考数学试卷(含答案),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









