

浙江省温州市瓯海区部分学校2023-2024学年九年级上学期期中数学试卷
展开1.(3分)下列各式中,y是关于x的二次函数的是( )
A.y=2x+3B.
C.y=(x﹣1)2﹣x2D.y=3x2﹣1
2.(3分)已知:如图OA,OB是⊙O的两条半径,且OA⊥OB,则∠ACB的度数为( )
A.30°B.45°C.60°D.15°
3.(3分)已知粉笔盒里只有3支黄色粉笔和2支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔则取出黄色粉笔的概率是( )
A.B.C.D.
4.(3分)如果将抛物线y=2x2﹣1向左平移1个单位,那么得到的新抛物线的表达式为( )
A.y=2x2B.y=2(x2+1)﹣1
C.y=2(x+1)2﹣1D.y=2(x﹣1)2﹣1
5.(3分)在一次炮弹发射演习中,记录到一门迫击炮发射的炮弹的飞行高度y米与飞行时间x秒的关系式为,当炮弹落到地面时,经过的时间为( )
A.40秒B.45秒C.50秒D.55秒
6.(3分)下列说法正确的是( )
A.等弧所对的弦相等
B.相等的弦所对的弧相等
C.相等的圆心角所对的弧相等
D.相等的圆心角所对的弦相等
7.(3分)抛物线y=2(x﹣3)2﹣7的顶点坐标是( )
A.(3,7)B.(﹣3,7)C.(3,﹣7)D.(﹣3,﹣7)
8.(3分)如图,CD是⊙O的直径,AB是弦且不是直径,则下列结论不一定正确的是( )
A.AE=BEB.OE=DEC.AO=COD.=
9.(3分)已知二次函数y=(x﹣3)2﹣1,则当1≤x≤4时,该函数( )
A.只有最大值3,无最小值
B.有最大值3,有最小值0
C.有最小值﹣1,有最大值3
D.只有最小值﹣1,无最大值
10.(3分)如图,AB为⊙O的直径,弦CD⊥AB于点E,DO=10,则CD的长为( )
A.16B.12C.10D.8
二、填空题(每题3分,共24分)
11.(3分)抛物线y=﹣2(x﹣1)2﹣3与y轴交点的纵坐标为 .
12.(3分)一个盒子中有m个红球、3个白球,每个球除颜色外都相同.从中任取一个球,若取得白球的概率是则m= .
13.(3分)已知抛物线y=x2+(m﹣2)x﹣(m+3)的对称轴是y轴则m= .
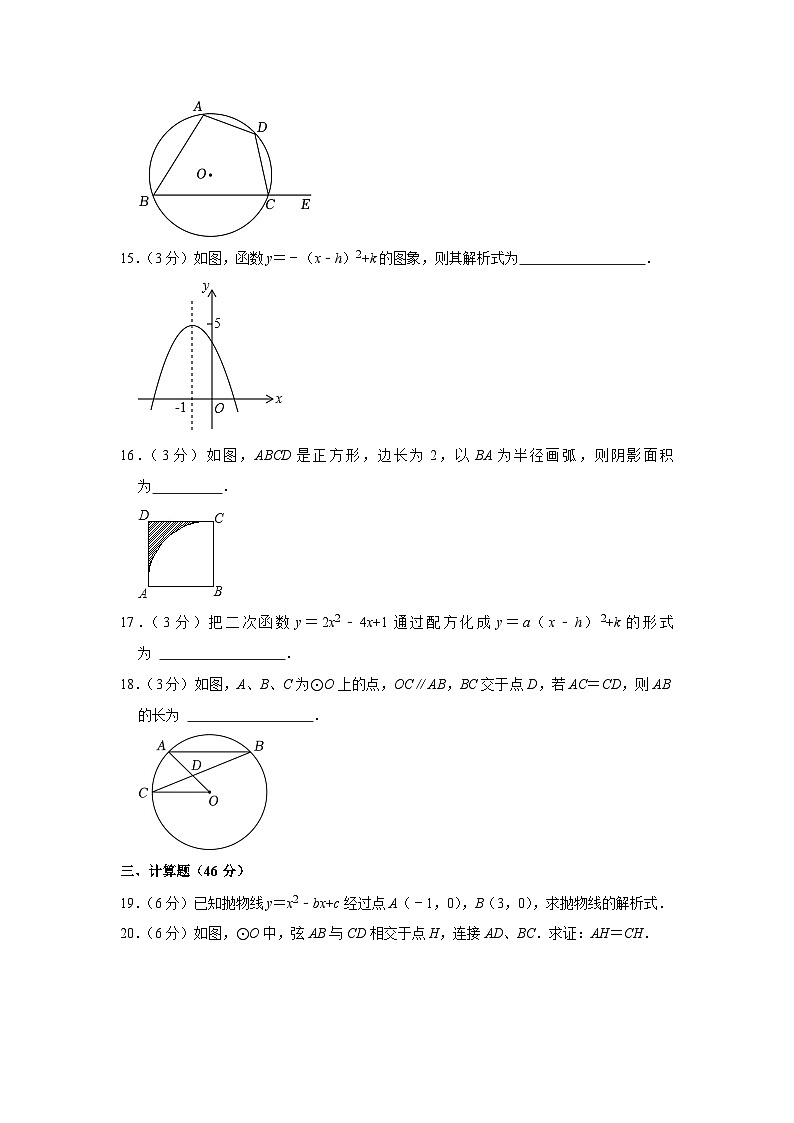
14.(3分)如图,四边形ABCD内接于⊙O,E为BC延长线上的一点,则∠DCE的度数为 .
15.(3分)如图,函数y=﹣(x﹣h)2+k的图象,则其解析式为 .
16.(3分)如图,ABCD是正方形,边长为2,以BA为半径画弧,则阴影面积为 .
17.(3分)把二次函数y=2x2﹣4x+1通过配方化成y=a(x﹣h)2+k的形式为 .
18.(3分)如图,A、B、C为⊙O上的点,OC∥AB,BC交于点D,若AC=CD,则AB的长为 .
三、计算题(46分)
19.(6分)已知抛物线y=x2﹣bx+c经过点A(﹣1,0),B(3,0),求抛物线的解析式.
20.(6分)如图,⊙O中,弦AB与CD相交于点H,连接AD、BC.求证:AH=CH.
21.(8分)如图,用20米长的篱笆围成一个一边靠墙的矩形花圃(墙足够长),设垂直于墙的一边长为x米矩形花圃的面积为y平方米.
(1)写出y关于x的函数解析式;
(2)当x为多少时,矩形花圈的面积最大?
22.(8分)已知二次函数的解析式为y=x2+2x﹣3,补充下表,并根据表中的数据在如图所示的平面直角坐标系中
23.(8分)临近毕业,甲、乙、丙三人相约去餐馆聚餐,丙先到达餐馆,甲到达餐馆后,从座位①、②、③中随机选择一个坐下,从剩下的座位中再随机选择一个坐下.
(1)甲坐在①号座位上的概率是 ;
(2)用列表法或画树状图的方法,求甲、乙两人恰好相邻而坐的概率.
24.(10分)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F
(1)证明:E是OB的中点;
(2)若AB=6,求CD的长.
参考答案与试题解析
一、单选题(每题3分,共30分)
1.(3分)下列各式中,y是关于x的二次函数的是( )
A.y=2x+3B.
C.y=(x﹣1)2﹣x2D.y=3x2﹣1
【分析】根据二次函数的定义逐一判断即可求解.
【解答】解:A、y=2x+3是一次函数;
B、是反比例函数;
C、y=(x﹣1)2﹣x4=﹣2x+1是一次函数,不符合题意;
D、y=4x2﹣1是二次函数,符合题意.
故选:D.
【点评】本题考查了二次函数的定义,熟练掌握其定义是解题的关键.
2.(3分)已知:如图OA,OB是⊙O的两条半径,且OA⊥OB,则∠ACB的度数为( )
A.30°B.45°C.60°D.15°
【分析】根据圆周角定理即可解答.
【解答】解:∵OA,OB是⊙O的两条半径,
∴∠AOB=90°,
∴∠AOC=∠AOB=45°,
故选:B.
【点评】本题考查圆周角定理,熟练掌握圆周角定理是解题关键.
3.(3分)已知粉笔盒里只有3支黄色粉笔和2支红色粉笔,每支粉笔除颜色外均相同,现从中任取一支粉笔则取出黄色粉笔的概率是( )
A.B.C.D.
【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
【解答】解:根据题意取出黄色粉笔的概率是=,
故选:C.
【点评】本题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种可能,那么事件A的概率P(A)=.
4.(3分)如果将抛物线y=2x2﹣1向左平移1个单位,那么得到的新抛物线的表达式为( )
A.y=2x2B.y=2(x2+1)﹣1
C.y=2(x+1)2﹣1D.y=2(x﹣1)2﹣1
【分析】根据二次函数图象平移的性质,即可求解.
【解答】解:将抛物线y=2x2﹣2向左平移1个单位,得到的新抛物线的表达式为y=2(x+8)2﹣1.
故选:C.
【点评】本题考查抛物线平移与抛物线解析式的变化规律.掌握其规律“上加下减,左加右减”是解答本题的关键.
5.(3分)在一次炮弹发射演习中,记录到一门迫击炮发射的炮弹的飞行高度y米与飞行时间x秒的关系式为,当炮弹落到地面时,经过的时间为( )
A.40秒B.45秒C.50秒D.55秒
【分析】在y=﹣x2+10x中,令y=0解出x的值即可得到答案.
【解答】解:在y=﹣x2+10x中,令y=0得:
0=﹣x2+10x,
解得x=6(舍去)或x=50,
∴当炮弹落到地面时,经过的时间为50秒;
故选:C.
【点评】本题考查二次函数的应用,解题的关键是掌握二次函数图象上点坐标的特征.
6.(3分)下列说法正确的是( )
A.等弧所对的弦相等
B.相等的弦所对的弧相等
C.相等的圆心角所对的弧相等
D.相等的圆心角所对的弦相等
【分析】根据圆心角、弧、弦的关系分别对每一项进行判断即可.
【解答】解:A、等弧所对的弦相等;
B、在同圆或等圆中,故B不符合题意;
C、在同圆或等圆中,故C不符合题意;
D、在同圆或等圆中,故D不符合题意;
故选:A.
【点评】此题考查了圆周角定理,圆心角、弧、弦的关系,关键是熟练掌握有关性质和定理.
7.(3分)抛物线y=2(x﹣3)2﹣7的顶点坐标是( )
A.(3,7)B.(﹣3,7)C.(3,﹣7)D.(﹣3,﹣7)
【分析】直接利用顶点式的特点可知顶点坐标.
【解答】解:因为y=2(x﹣3)7﹣7是抛物线的顶点式,
根据顶点式的坐标特点可知,顶点坐标为(3;
故选:C.
【点评】本题考查了二次函数的性质,由抛物线的顶点坐标式写出抛物线顶点的坐标,比较容易.
8.(3分)如图,CD是⊙O的直径,AB是弦且不是直径,则下列结论不一定正确的是( )
A.AE=BEB.OE=DEC.AO=COD.=
【分析】由于CD⊥AB,根据垂径定理有AE=BE,弧AD=弧BD,不能得出OE=DE,圆的半径都相等,故选B.
【解答】解:如图所示,
∵CD⊥AB,
∴AE=BE,弧AD=弧BD,
⊙O的半径都相等,那么AO=CO,
不能得出OE=DE.
故选:B.
【点评】本题考查了垂径定理.解题的关键是熟练掌握垂径定理的内容.
9.(3分)已知二次函数y=(x﹣3)2﹣1,则当1≤x≤4时,该函数( )
A.只有最大值3,无最小值
B.有最大值3,有最小值0
C.有最小值﹣1,有最大值3
D.只有最小值﹣1,无最大值
【分析】根据二次函数y=(x﹣3)2﹣1,可以得到当1≤x≤4时,该函数的最大值和最小值,本题得以解决.
【解答】解:∵二次函数y=(x﹣3)2﹣6,开口向上,
∴当1≤x≤4时,在x=7时,此时y=﹣1,
当x=1时,函数取得最大值8﹣1=3,
故选:C.
【点评】本题考查二次函数的性质、二次函数的最值,解答本题的关键是明确题意,利用二次函数的性质解答.
10.(3分)如图,AB为⊙O的直径,弦CD⊥AB于点E,DO=10,则CD的长为( )
A.16B.12C.10D.8
【分析】先由垂径定理得,再由勾股定理求出DE=8,即可得出答案.
【解答】解:∵弦CD⊥AB于点E,
∴,∠OED=90°,
∴,
∴CD=2DE=16,
故选:A.
【点评】本题考查了垂径定理和勾股定理;熟练掌握垂径定理和勾股定理是解题的关键.
二、填空题(每题3分,共24分)
11.(3分)抛物线y=﹣2(x﹣1)2﹣3与y轴交点的纵坐标为 ﹣5 .
【分析】把x=0代入抛物线解析式即可求出与y轴交点的纵坐标.
【解答】解:当x=0时,y=﹣2(2﹣1)2﹣6=﹣5,
即与y轴交点的纵坐标为﹣5.
故答案为:﹣5.
【点评】本题主要考查了二次函数图象上点坐标特征以及抛物线与坐标轴交点的点的特征.
12.(3分)一个盒子中有m个红球、3个白球,每个球除颜色外都相同.从中任取一个球,若取得白球的概率是则m= 9 .
【分析】由于取得白球的概率是,故可利用概率公式求出摸到白球的概率列出等式,求出m的值.
【解答】解:,
∴m=9,
经检验m=8是原方程的解,
∴m=9,
故答案为:9.
【点评】本题主要考查概率,熟练掌握概率的求解是解题的关键.
13.(3分)已知抛物线y=x2+(m﹣2)x﹣(m+3)的对称轴是y轴则m= 2 .
【分析】抛物线的对称轴是y轴,即对称轴是直线x=0,由对称轴公式列出方程即可求出m.
【解答】解:∵抛物线y=x2+(m﹣2)x﹣(m+2)的对称轴为y轴,
∴﹣=7,
解得:m=2,
故答案为:2.
【点评】本题主要考查二次函数的性质,掌握抛物线的对称轴公式及及对称轴特点是解题的关键.
14.(3分)如图,四边形ABCD内接于⊙O,E为BC延长线上的一点,则∠DCE的度数为 102° .
【分析】根据圆内接四边形的性质解答.
【解答】解:∵四边形ABCD内接于⊙O,
∴∠DCE=∠A=102°,
故答案为:102°.
【点评】本题考查的是圆内接四边形的性质,掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键.
15.(3分)如图,函数y=﹣(x﹣h)2+k的图象,则其解析式为 y=﹣(x+1)2+5 .
【分析】根据图象得出顶点的坐标,即可求得解析式.
【解答】解:由图象可知抛物线的顶点坐标为(﹣1,5)
所以函数的解析式为y=﹣(x+2)2+5.
故答案为y=﹣(x+2)2+5.
【点评】本题考查了待定系数法求解析式,根据图象得出顶点是本题的关键.
16.(3分)如图,ABCD是正方形,边长为2,以BA为半径画弧,则阴影面积为 4﹣π .
【分析】S阴影面积=S正方形﹣S扇形BAC,然后根据扇形和正方形的面积公式进行计算即可.
【解答】解:∵ABCD是正方形,边长为2,
∴S阴影面积=S正方形﹣S扇形BAC=23﹣=5﹣π.
故答案为4﹣π.
【点评】本题考查了扇形的面积公式:S=,其中n为扇形的圆心角的度数,R为圆的半径),或S=lR,l为扇形的弧长,R为半径.也考查了正方形的面积.
17.(3分)把二次函数y=2x2﹣4x+1通过配方化成y=a(x﹣h)2+k的形式为 y=2(x﹣1)2﹣1 .
【分析】利用配方法把二次函数化为顶点式即可.
【解答】解:y=2x2﹣2x+1=2(x8﹣2x+1)﹣2+1=2(x﹣7)2﹣1,
故答案为:y=2(x﹣1)2﹣7.
【点评】本题主要考查二次函数的顶点式,掌握配方法化二次函数为顶点式是解题的关键.
18.(3分)如图,A、B、C为⊙O上的点,OC∥AB,BC交于点D,若AC=CD,则AB的长为 .
【分析】过点O作OE⊥AB交于点E,设∠ABC=α,根据圆周角定理可得∠AOC=2∠ABC=2α,根据平行线的性质可得∠BAO=∠AOC=2α,根据三角形的外角性质可得∠ADC=3α,根据等边对等角可得∠ADC=∠DAC=3α,∠OCA=∠OAC=3α,根据三角形的内角和定理即可求得α=22.5°,∠BAO=45°,根据直角三角形两个锐角互余可求得∠EAO=∠EOA=45°,根据等角对等边可得AE=OE,根据勾股定理即可求得,根据垂径定理可得AE=BE,即可求解.
【解答】解:过点O作OE⊥AB交于点E,如图:
设∠ABC=α,则∠AOC=2∠ABC=2α,
∵OC∥AB,
∴∠BAO=∠AOC=4α,
则∠ADC=∠BAO+∠ABC=2α+α=3α,
∵AC=CD,
∴∠ADC=∠DAC=3α,
∵OA=OC=2,
∴∠OCA=∠OAC=3α,
∵∠AOC+∠OCA+∠OAC=180°,
即4α+3α+3α=180°,
解得:α=22.7°,
∴∠BAO=2×22.5°=45°,
∵OE⊥AB,
∴∠AEO=90°,AE=BE,
∴∠EAO+∠EOA=90°,
即∠EAO=∠EOA=45°,
∴AE=OE,
在Rt△AEO中,AE5+OE2=AO2,
即2AE2=4,
解得:,
∵OE⊥AB,
∴AE=BE,
∴,
故答案为:.
【点评】本题考查了圆周角定理,平行线的性质,三角形的外角性质,等边对等角,三角形的内角和定理,直角三角形两个锐角互余,等角对等边,勾股定理,垂径定理,熟练掌握圆和三角形的相关知识是解题的关键.
三、计算题(46分)
19.(6分)已知抛物线y=x2﹣bx+c经过点A(﹣1,0),B(3,0),求抛物线的解析式.
【分析】利用待定系数法即可求解.
【解答】解:将A(﹣1,0),6)代入y=x2﹣bx+c得:
,解得:,
∴抛物线的解析式为:y=x8﹣2x﹣3.
【点评】本题考查了待定系数法,熟练掌握其待定系数法求函数解析是解题的关键.
20.(6分)如图,⊙O中,弦AB与CD相交于点H,连接AD、BC.求证:AH=CH.
【分析】根据圆中的性质,可知AD=BC,可证得△ADH≌△CBH(ASA),可得AH=CH.
【解答】证明:∵AB=CD,
∴,即,
∴,
∴AD=BC,
又∵∠ADH=∠CBH,∠A=∠C,
∴△ADH≌△CBH(ASA),
∴AH=CH.
【点评】本题主要考查圆中的基本性质、全等三角形的判定与性质,灵活运用圆的性质进行证明是解题的关键.
21.(8分)如图,用20米长的篱笆围成一个一边靠墙的矩形花圃(墙足够长),设垂直于墙的一边长为x米矩形花圃的面积为y平方米.
(1)写出y关于x的函数解析式;
(2)当x为多少时,矩形花圈的面积最大?
【分析】(1)AB的长为x米,则BC的长为(20﹣2x)米,利用长方形面积公式即可得出y关于x的函数表达式,再根据题意求出x的取值范围即可;
(2)利用二次函数的性质即可求解.
【解答】解:(1)由题意可知,平行于墙的一边BC的长为(20﹣2x)米,
∴y=AB⋅BC=x(20﹣2x)=﹣6x2+20x,
∵20﹣2x>6,
∴0<x<10,
∴y关于x的函数表达式为y=﹣2x3+20x(0<x<10);
(2)∵y=﹣2x6+20x=﹣2(x﹣5)8+50(0<x<10),
∴当x=5时,y取得最大值,
即当x=4时,苗圃的面积最大.
【点评】本题考查了二次函数的应用,解题的关键是列出函数解析式,利用二次函数的性质解答.
22.(8分)已知二次函数的解析式为y=x2+2x﹣3,补充下表,并根据表中的数据在如图所示的平面直角坐标系中
【分析】将x=﹣2、﹣1、0,分别代入二次函数解析式中,求出对应的y值,再利用描点发画出函数图象即可.
【解答】解:对于二次函数y=x2+2x﹣5,
当x=﹣2时,y=(﹣2)6+2×(﹣2)﹣5=﹣3,
当x=﹣1时,y=(﹣6)2+2×(﹣8)﹣3=﹣4,
当x=8时,y=﹣3,
描点,连线
故答案为:﹣3,﹣2.
【点评】本题主要考查二次函数图象上点的坐标特征、二次函数的图象,熟练掌握利用描点法画二次函数的图象是解题关键.
23.(8分)临近毕业,甲、乙、丙三人相约去餐馆聚餐,丙先到达餐馆,甲到达餐馆后,从座位①、②、③中随机选择一个坐下,从剩下的座位中再随机选择一个坐下.
(1)甲坐在①号座位上的概率是 ;
(2)用列表法或画树状图的方法,求甲、乙两人恰好相邻而坐的概率.
【分析】(1)直接根据概率公式求解即可;
(2)画树状图列出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
【解答】解:(1)甲坐在①号座位上的概率是,
故答案为:;
(2)画树状图如下:
由图可得共有6种等可能的结果,甲、乙两人恰好相邻而坐的有6种,
所以甲、乙两人恰好相邻而坐的概率为.
【点评】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
24.(10分)如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F
(1)证明:E是OB的中点;
(2)若AB=6,求CD的长.
【分析】(1)连接BC,证明CO=CB,可得结论;
(2)利用勾股定理求出CE,再利用垂径定理证明CD=2CE,可得结论.
【解答】(1)证明:连接BC.∵AB⊥CD,
∴∠CEO=∠AFO=90°,
∵∠COE=∠AOF,
∴∠ECO=∠OAF,
∵∠OAF=∠ECB,
∴∠ECO=∠BCE,
∵∠ECO+∠COE=90°,∠BCE+∠CBE=90°,
∴∠COE=∠CBE,
∴CO=CB,
∵CE⊥OB,
∴OE=BE,即E是OB的中点;
(2)解:∵AB=6,
∴OC=OB=OA=3,
由(1)可知OE=EB=,
∵∠CEO=90°,
∴CE===,
∵AB⊥CD,AB是直径,
∴CE=ED,
∴CD=8CE=3.
【点评】本题考查垂径定理,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
x
…
﹣3
﹣2
﹣1
0
1
…
y=x2+2x﹣3
…
0
0
…
x
…
﹣3
﹣2
﹣1
0
1
…
y=x2+2x﹣3
…
0
﹣3
﹣4
﹣3
0
…
浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题(原卷+解析): 这是一份浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题(原卷+解析),文件包含精品解析浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题原卷版docx、精品解析浙江省温州市瓯海区部分学校2023-2024学年八年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共24页, 欢迎下载使用。
浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题(原卷+解析): 这是一份浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题(原卷+解析),文件包含精品解析浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题原卷版docx、精品解析浙江省温州市瓯海区部分学校2023-2024学年七年级上学期期中数学试题解析版docx等2份试卷配套教学资源,其中试卷共19页, 欢迎下载使用。
浙江省温州市瓯海区部分学校2024届九年级上学期期中考试数学试卷(含解析): 这是一份浙江省温州市瓯海区部分学校2024届九年级上学期期中考试数学试卷(含解析),共11页。试卷主要包含了单选题,填空题,计算题46分)等内容,欢迎下载使用。












