



- 人教版数学《垂线》PPT课件 课件 2 次下载
- 人教版数学《同位角、内错角、同旁内角》PPT课件 课件 3 次下载
- 人教版数学《平行线》PPT课件 课件 3 次下载
- 人教版数学《平行线的判定》PPT课件 课件 2 次下载
- 人教版数学《平行线的判定》PPT课件 课件 2 次下载
初中数学人教版七年级下册5.1.1 相交线一等奖ppt课件
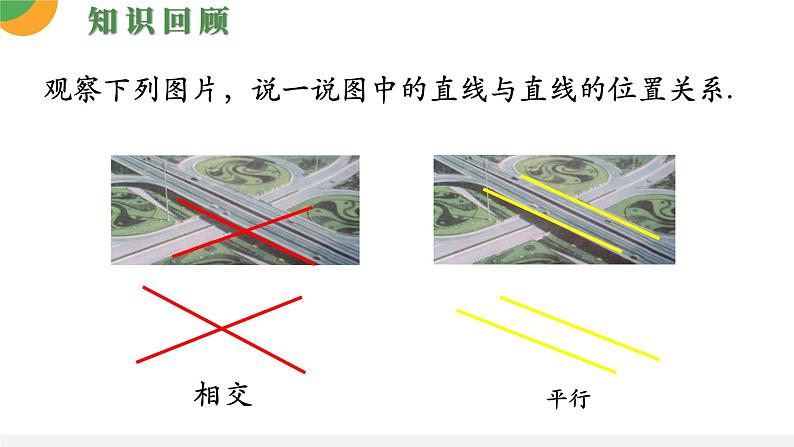
展开观察下列图片,说一说图中的直线与直线的位置关系.
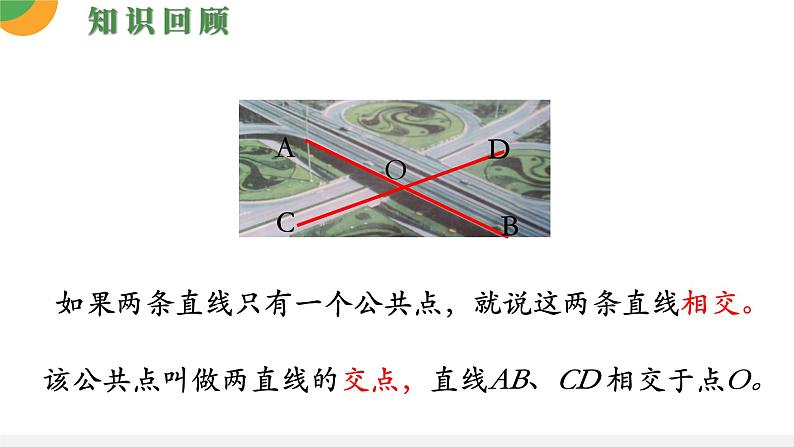
如果两条直线只有一个公共点,就说这两条直线相交。
该公共点叫做两直线的交点,直线AB、CD 相交于点O。
如图,观察剪刀剪布的过程,体会角的变化。
如果把剪子的构造抽象成一个几何图形,会是什么样的图形?请你画一画。
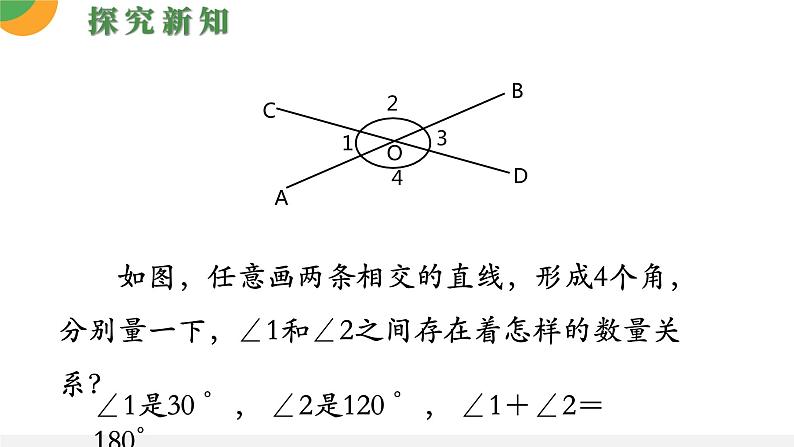
如图,任意画两条相交的直线,形成4个角,分别量一下,∠1和∠2之间存在着怎样的数量关系?
∠1是30 °, ∠2是120 °, ∠1+∠2=180°
1.概念 :两个角之间有一条公共边,它们的另一边互为反向延长线(两角互补),具有这种关系的两个角互为邻补角。
2.性质 :两角之和为180°,两角互补
如图,分别量一下,∠1和∠3之间存在着怎样的数量关系?
∠1是30 °, ∠3是30 °, ∠1=∠3
如图,∠1和∠3之间存在着怎样的位置关系?
∠1和∠3有个公共顶点O,并且∠1的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
1.概念:两角之间有一个公共顶点O,并且一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
如图,直线AB,CD相交于点O,OE是∠BOD内部的一条射线.(1)分别写出∠AOE和∠AOD的邻补角;
解:(1)∠AOE的邻补角为∠BOE;∠AOD的邻补角为∠BOD和∠AOC.
如图,直线AB,CD相交于点O,OE是∠BOD内部的一条射线。(2)写出图中所有的对顶角。
解: (2)对顶角有∠AOC与∠BOD,∠AOD与∠BOC.
如图,直线a, b相交,∠1 = 40°,∠2,∠3,∠4的度数.
解:由邻补角的定义, 得∠2 = 180°-∠1 = 180°-40°=140°;由对顶角相等, 得∠3 = ∠1 = 40° , ∠4 = ∠2 = 140°
如图,直线a,b相交于点O, 1: 2 = 2: 7 , 求∠1, ∠2 ,∠3 ,∠4 的度数.
解:设∠1=2x°,则∠2=7x °根据邻补角的定义,得 2x+7x=180 x=20则∠1=40°, ∠2=140°根据对顶角相等,得∠3=40°, ∠4=140°
另一边互为反向延长线
1. 下列选项中,∠1与∠2互为邻补角的是( )
2. 如图,∠1与∠2是对顶角的是( )
3. 如图,小强和小丽一起玩跷跷板,横板AB绕O上下转动,当小强从A到A′的位置时,∠AOA′=45°,则∠BOB′的度数为______,理由是___________.
4.如图所示,直线AB,CD相交于点O,∠AOC∶∠AOD=2∶3,则∠BOD= °.
5.如图,直线AB,CD,EF相交于点O. (1)写出∠AOC, ∠BOE的邻补角;
解:(1)∠AOC的邻补角是∠AOD和∠COB;∠BOE的邻补角是∠EOA和∠BOF。
5.如图,直线AB,CD,EF相交于点O。 (2)写出∠DOA, ∠EOC的对顶角;
解:(2)∠DOA的对顶角是∠COB; ∠EOC的对顶角是∠DOF.
解 (3)∠BOD=∠AOC= 50°; ∠COB=180°-∠AOC=130°.
5.如图,直线AB,CD,EF相交于点O。(3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
思考:如图,取两根木条a,b,将它们钉在一起,并把它们想象成两条直线,就得到一个相交线的模型.你能说出其中的一些邻补角与对顶角吗?两根木条所成的角中,如果∠α=35°,其他三 个角各等于多少度?如果∠α等于90°,115°,m°呢?
七年级下册5.1.1 相交线课堂教学ppt课件: 这是一份七年级下册5.1.1 相交线课堂教学ppt课件,共22页。PPT课件主要包含了巩固新知,∠2=180°-∠1,=180°-40°,=140°,由对顶角相等可得,∠3=∠1=40°,∠4=∠2=140°,两个角互为邻补角,互为反向延长线等内容,欢迎下载使用。
人教版七年级下册5.1.1 相交线优秀ppt课件: 这是一份人教版七年级下册5.1.1 相交线优秀ppt课件,文件包含精品原创人教版数学七年级下册511《相交线》课件pptx、精品原创人教版数学七年级下册511《相交线》练习docx、精品原创人教版数学七年级下册511《相交线》教案docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
人教版七年级下册5.1.1 相交线精品ppt课件: 这是一份人教版七年级下册5.1.1 相交线精品ppt课件,共16页。PPT课件主要包含了邻补角,反向延长线,∠2∠3,对顶角,对顶角的性质,猜想对顶角相等,对顶角相等,nn-1等内容,欢迎下载使用。














