
山东省青岛市市北区2023-2024学年八年级上学期11月期中数学试题
展开(考试时间:120分钟;满分:120分)
说明:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,共23题. 第Ⅰ卷为选择题,共8小题,24分;第Ⅱ卷为填空题、作图题、解答题,共 15 小题,96分.
2. 所有题目均在答题卡上作答,在试题上作答无效.
第Ⅰ卷(共24分)
一、选择题(本大题共8小题,每小题3分,共24分)
在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 下列各数是无理数的有
36, 2.030030003……(相邻两个3之间0的个数逐次加 1), 17,π, ……,- 5.
A. 2个 B. 3个 C. 4个 D. 5个
2. 满足 a²+b²=c²的三个正整数a、b、c,被称为勾股数。下列各组数是勾股数的是
A. 7, 24, 25 B. 3²,4²,5² C. 1.5, 2, 2.5 D.3,4,7
3.-22=
A. 4 B. 2 C. ±2 D. -2
4.若点P(m+3,m-2)在平面直角坐标系的x轴上,则点 P的坐标为
A. (0, 5) B. (5, 0)
C. (-5, 0) D. (0, -5)
5. 关于一次函数y=-2x+3,下列结论正确的是
A. 图象不经过第二象限
B. 图象与x轴的交点是(0,3)
C. 将一次函数y=-2x+3的图象向上平移3个单位长度后,所得图象的函数表达式为y=-2x+6
D. 点(x₁,y₁)和(x₂,y₂)在一次函数y=-2x+3的图象上, 若 x₁
第1页 (共6页)
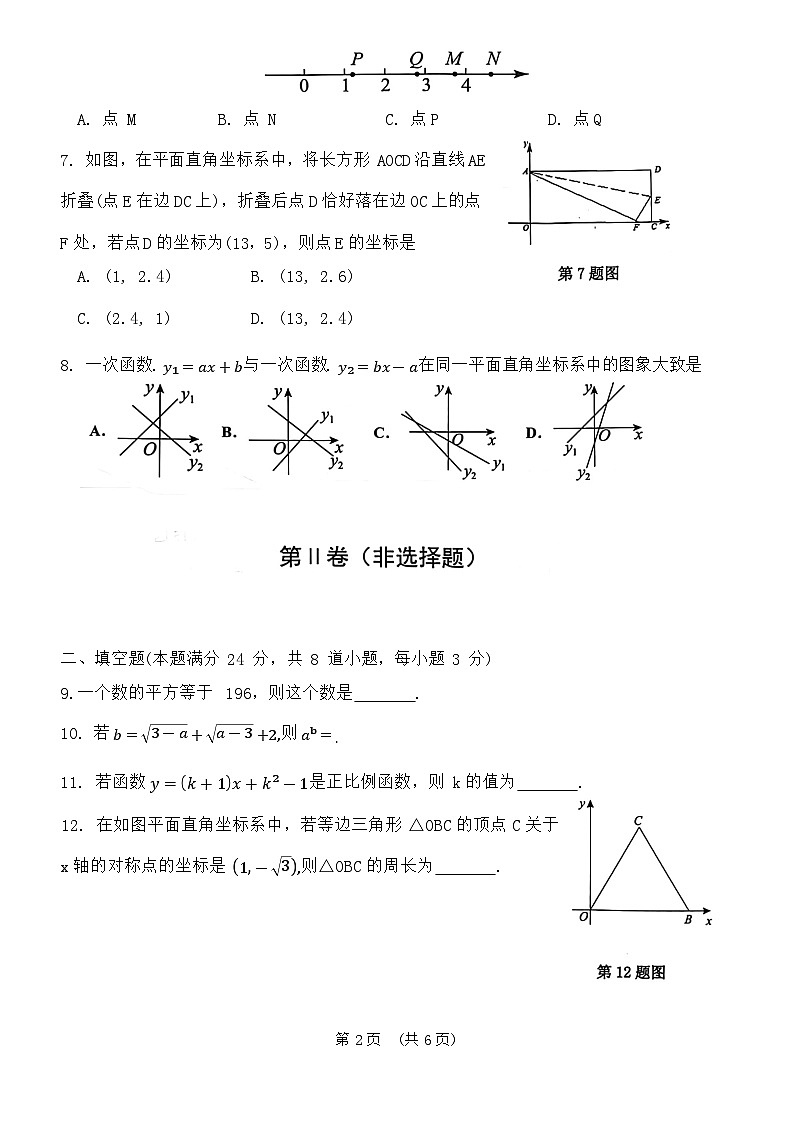
A. 点 M B. 点 N C. 点P D. 点Q
7. 如图,在平面直角坐标系中,将长方形 AOCD沿直线AE折叠(点E在边DC上),折叠后点D恰好落在边OC上的点F处,若点D的坐标为(13,5),则点E的坐标是
A. (1, 2.4) B. (13, 2.6)
C. (2.4, 1) D. (13, 2.4)
8. 一次函数. y₁=ax+b与一次函数. y₂=bx-a在同一平面直角坐标系中的图象大致是
二、填空题(本题满分 24 分,共 8 道小题,每小题 3 分)
9.一个数的平方等于 196,则这个数是 .
10. 若 b=3-a+a-3+2,则 aᵇ=.
11. 若函数 y=k+1x+k²-1是正比例函数,则k的值为 .
12. 在如图平面直角坐标系中,若等边三角形△OBC的顶点C关于x轴的对称点的坐标是 1-3,则△OBC的周长为 .
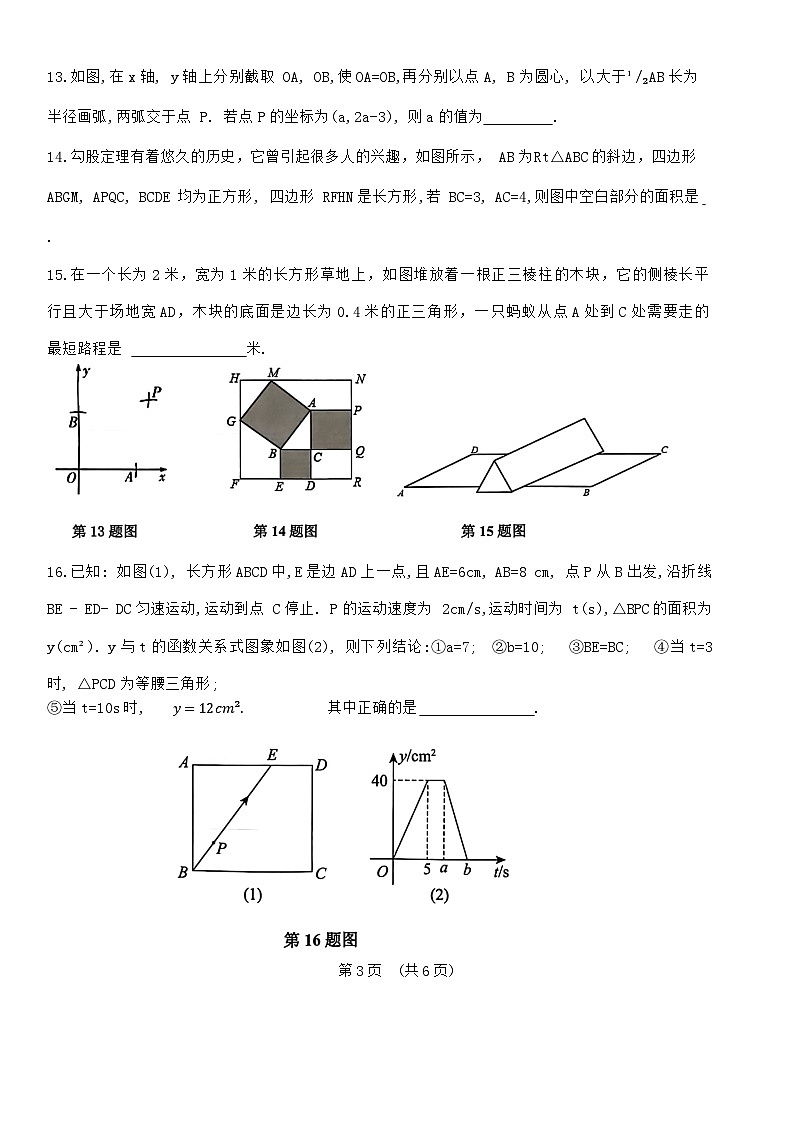
第2页 (共6页)13.如图,在x轴, y轴上分别截取 OA, OB,使OA=OB,再分别以点A, B为圆心, 以大于¹/₂AB长为半径画弧,两弧交于点 P. 若点P的坐标为(a,2a-3), 则a的值为 .
14.勾股定理有着悠久的历史,它曾引起很多人的兴趣,如图所示,AB为 Rt△ABC的斜边,四边形 ABGM, APQC, BCDE 均为正方形, 四边形 RFHN是长方形,若 BC=3, AC=4,则图中空白部分的面积是 .
15.在一个长为2米,宽为1米的长方形草地上,如图堆放着一根正三棱柱的木块,它的侧棱长平行且大于场地宽AD,木块的底面是边长为0.4米的正三角形,一只蚂蚁从点A处到C处需要走的最短路程是 米.
16.已知: 如图(1), 长方形ABCD中,E是边AD上一点,且AE=6cm, AB=8 cm, 点P从B出发,沿折线BE - ED- DC匀速运动,运动到点 C停止. P的运动速度为 2cm/s,运动时间为 t(s),△BPC的面积为y(cm²). y与t的函数关系式图象如图(2), 则下列结论:①a=7; ②b=10; ③BE=BC; ④当t=3时, △PCD为等腰三角形;
⑤当t=10s时, y=12cm². 其中正确的是 .
第3页 (共6页)三、作图题(本题满分 8分)
17.如图,在4×4的方格纸中,每个小正方形的边长都为 1,△ABC的三个顶点都在格点上,已知 AC=25,BC=5.
(1) AB的长为 .
(2) 在所给方格纸中画出△ABC.
(3)判断△ABC的形状,并说明理由.
四、解答题(共64分)
18. 计算下列各题(本题满分 16分)
(1)观察图形,回答问题
①计算x 的值。
② 计算正数a 的值。
28+18-42
342÷7-13×18+24
432+52-5+11×11-5
19. (本题满分8分)
某条东西走向的道路限速70公里/时。如图,一辆小汽车在这条道路上沿直线行驶,某一时刻刚好行驶到C处,C处位于车速检测仪A处的正北方30米。2秒钟后,这辆小汽车到达B处,此时测得小汽车与车速测检测仪之间的距离是50米, 请通过计算说明这辆小汽车是否超速。
第4页 (共6页)20. (本题满分8分)
如图1,由8个同样大小的正方体组成一个魔方(大正方体),魔方的体积为64.
(1) 求出这个魔方的棱长;
(2) 图1中阴影部分是一个正方形ABCD,求出阴影部分的面积和边长;
(3) 把正方形ABCD放到数轴上,如图2,使点A与-1重合。
请直接写出点 D在数轴上所表示的数.
21. (本题满分8分)
五子棋的比赛规则是:只要同色5子连成一条直线为胜利.如图是两人玩的一盘棋,若白棋①的位置是(1,-5), 黑棋②的位置是(2,-4)。解答下列问题:
(1)白棋③的位置是 ;
(2)如果现在轮到黑棋走,黑棋放在 位置就获得胜利了;
(3)如果现在轮到白棋走,白棋放在 位置就获得胜利了.
(4) 在(2) 的条件下,黑棋获胜了。
①设此时黑色5子连成直线的表达式是 y=ax+b.则方程ax+b=0的解是 .
②若黑色5子连成直线的表达式中y<0,则x 的取值范围是 .
第5页 (共6页)22. (本题满分 12分)
甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程(米)与甲出发的时间(秒)的函数图象,请根据题意解答下列问题:
(1) 在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2) 乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;
(3) 乙出发 秒后与甲第一次相遇;
(4) x= 秒时, 甲乙两人相距50米。
23. (本题满分 12分)
如图,平面直角坐标系xOy中,直线 y=-43x+k与x轴、y轴围成的△AOB 的周长为12,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴的点C处.
(1)求k的值;
(2)求点C 的坐标和直线DC 的解析式.
第6页 (共6页)
山东省青岛市市北区2023-2024学年九年级上学期1月期末数学试题: 这是一份山东省青岛市市北区2023-2024学年九年级上学期1月期末数学试题,共4页。
山东省青岛市市北区2023-2024学年九年级上学期1月期末数学试题: 这是一份山东省青岛市市北区2023-2024学年九年级上学期1月期末数学试题,共7页。
山东省青岛市市北区2023-2024学年七年级上学期11月期中数学试题: 这是一份山东省青岛市市北区2023-2024学年七年级上学期11月期中数学试题,共3页。












