2024版新教材高中数学第四章立体几何初步4.5几种简单几何体的表面积和体积4.5.2几种简单几何体的体积课件湘教版必修第二册

这是一份2024版新教材高中数学第四章立体几何初步4.5几种简单几何体的表面积和体积4.5.2几种简单几何体的体积课件湘教版必修第二册，共38页。

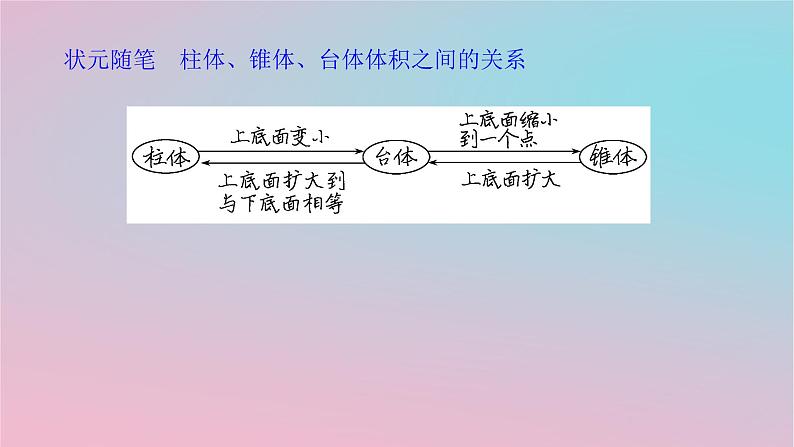
4.5.2　几种简单几何体的体积新知初探·课前预习题型探究·课堂解透新知初探·课前预习教材要点要点　柱、锥、台、球的体积公式Sh  状元随笔　柱体、锥体、台体体积之间的关系 √√×√ 答案：A  答案：C 4．若球的表面积为4π，则体积为________．  题型探究·课堂解透 答案：D (2)如图所示，已知E，F分别是棱长为a的正方体ABCD­-A1B1C1D1的棱A1A，CC1的中点，则四棱锥C1­-B1EDF的体积为________．   答案：A 方法归纳简单几何体体积的求法(1)直接法：直接套用体积公式求解．(2)等体积转移法：在三棱锥中，每一个面都可作为底面．为了求解的方便，我们经常需要换底，此法在求点到平面的距离时也常用到．(3)分割法：在求一些不规则的空间图形的体积时，我们可以将其分割成规则的、易于求解的空间图形．(4)补形法：对一些不规则(或难求解)的空间图形，我们可以通过补形，将其补为规则(或易于求解)的空间图形．  答案：A(2)三棱锥A-­BCD的高为4，底面BCD为直角三角形，两直角边BD和CD的长分别为5，3，则该三棱锥的体积为(　　)A．60 B．30 C．20 D．10答案：D (3)已知圆台的上、下底面半径和高的比为1∶4∶4，母线长为10，则圆台的体积为________．224π   答案：A(2)棱长为a的正四面体的各个顶点都在半径为R的球面上，则球的体积为________．  方法归纳常见几何体与球的切、接问题的解决策略(1)处理有关几何体外接球或内切球的相关问题时，要注意球心的位置与几何体的关系．一般情况下，由于球的对称性，球心总在特殊位置，比如中心、对角线的中点等．(2)解决此类问题的实质就是根据几何体的相关数据求球的直径或半径，关键是根据“切点”和“接点”，作出轴截面图，把空间问题转化为平面问题来计算．角度2　球的体积在实际中的应用例3　把半径分别为6 cm，8 cm，10 cm的三个铁球熔成一个铁球，则这个大铁球的半径是________ cm.12 方法归纳解决本题的关键是总体积不变．跟踪训练2　(1)圆柱形容器内部盛有高度为h的水，若放入两个直径为3 cm的铁球(球的半径与圆柱底面半径相等)后，水恰好淹没最上面的铁球(如图所示)，则h＝(　　)A．2 cm B．3 cmC．4 cm D．5 cm答案：A (2)一底面边长为4的正六棱柱，高为6，则它的外接球(正六棱柱的顶点都在此球面上)的体积为________．  题型 3　简单组合体的体积例4　如图所示，在棱长为4的正方体上底面中心位置打一个直径为2，深为4的圆柱形孔，求打孔后的几何体的表面积和体积．解析：正方体的表面积为S正方体＝4×4×6＝96，圆柱形孔的半径为1，高为4，∴圆柱的侧面积S圆柱侧＝2π×1×4＝8π，∴所求的表面积为S＝96＋8π－2π＝96＋6π，正方体的体积为V正方体＝4×4×4＝64，圆柱的体积为V圆柱＝4π，∴所求的体积为V＝64－4π.方法归纳求组合体的表面积与体积的关键是弄清组合体中各简单几何体的结构特征及组合形式，对于与旋转体有关的组合体问题，要根据条件分清各个简单几何体的底面半径及母线长，再分别代入公式求解．跟踪训练3　已知某几何体的直观图如图所示(单位：cm)，求这个几何体的体积为________cm3.10 易错辨析　忽略对侧面展开图的分类讨论致错例5　已知一个正三棱柱的侧面展开图是一个长为9 cm，宽为6 cm的矩形，则此正三棱柱的体积为______________cm3.  易错警示 答案：B解析：设正方体的棱长为a，则6a2＝96，∴a2＝16，∴a＝4，∴V正方体＝a3＝43＝64. 答案：B 3．如图所示，三棱锥的顶点为P，PA，PB，PC为三条侧棱，且PA，PB，PC两两互相垂直，又PA＝2，PB＝3，PC＝4，则三棱锥P­ABC的体积V＝________．4