高中人教A版 (2019)第三章 函数的概念与性质3.2 函数的基本性质备课课件ppt

这是一份高中人教A版 (2019)第三章 函数的概念与性质3.2 函数的基本性质备课课件ppt，共38页。PPT课件主要包含了预学案，共学案，函数的奇偶性❶，f－x＝fx，答案C，答案A，答案D，答案B等内容，欢迎下载使用。

f(－x)＝－f(x)
微点拨❶(1)函数的单调性是函数的“局部”性质，而奇偶性是函数的“整体”性质，只有对其定义域内的每一个x，都有f(－x)＝－f(x)(或f(－x)＝f(x))，才能说f(x)是奇(偶)函数．(2)函数y＝f(x)是奇函数或偶函数的一个必不可少的条件：定义域关于原点对称．若所给函数的定义域不关于原点对称，则这个函数是非奇非偶函数．例如，函数y＝x2在区间(－∞，＋∞)上是偶函数，但在区间[－1，2]上无奇偶性可言．(3)若f(－x)＝－f(x)且f(－x)＝f(x)，则f(x)既是奇函数又是偶函数，这样的函数有且只有一类，即f(x)＝0，x∈D，D是关于原点对称的实数集．若f(－x)≠－f(x)且f(－x)≠f(x)，则f(x)是非奇非偶函数．
【即时练习】　1．判断正误(正确的画“√”，错误的画“×”)(1)f(x)是定义在R上的函数，若f(－1)＝f(1)，则f(x)一定是偶函数．(　　)(2)对于函数y＝f(x)，若存在x，使f(－x)＝－f(x)，则函数y＝f(x)一定是奇函数.(　　)(3)若函数的定义域关于原点对称，则这个函数不是奇函数就是偶函数．(　　)
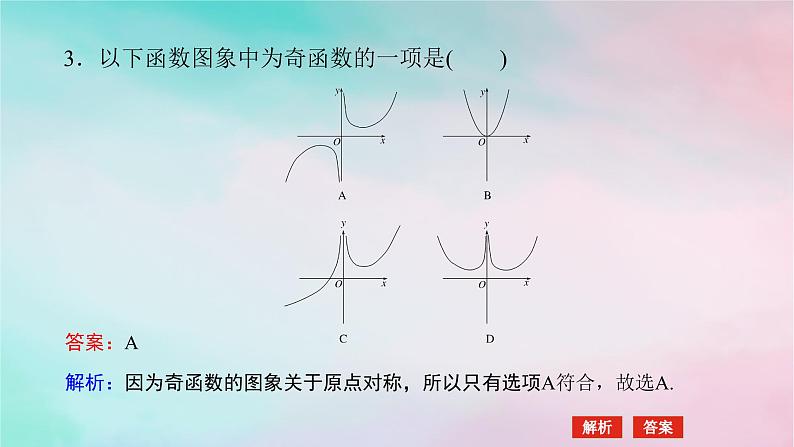
3．以下函数图象中为奇函数的一项是(　　)
解析：因为奇函数的图象关于原点对称，所以只有选项A符合，故选A.
【学习目标】　(1)理解奇函数、偶函数的定义．(2)了解奇函数、偶函数的图象特征．(3)能用定义判断函数的奇偶性．
【问题探究1】　观察下列两个函数的图象，据此回答下列问题：(1)这两个函数的图象有何共同特征？(2)对于上述两个函数， f(1) 与 f(－1) , f(2) 与 f(－2)，f(a) 与 f(－a) 有什么关系？由此可得到什么一般性的结论？
提示：(1)都关于y轴对称．(2)f(1)＝f(－1)，f(2)＝f(－2)，f(a)＝f(－a)．一般地，若函数y＝f(x)的图象关于y轴对称，当自变量任取定义域中的一对相反数时，对应的函数值相等．即f(－x)＝f(x)，满足这种性质的函数叫作偶函数．
【问题探究2】　观察下列两个函数的图象，据此回答下列问题：(1)这两个函数的图象有何共同特征？(2)对于上述两个函数， f(1) 与 f(－1) , f(2) 与 f(－2)，f(a) 与 f(－a) 有什么关系？由此可得到什么一般性的结论？
提示：(1)都关于原点对称．(2)f(1)＝－f(－1)，f(2)＝－f(－2)，f(a)＝－f(－a)．一般地，若函数y＝f(x)的图象关于原点对称，当自变量任取定义域中的一对相反数时，对应的函数值相反，f(－x)＝－f(x)，满足这种性质的函数叫做奇函数．
题后师说判断函数奇偶性的3种方法
题型 2 奇、偶函数的图象及应用例2　已知函数f(x)为定义在[－3，3]上的偶函数，其部分图象如图所示．(1)请作出函数f(x)在[0，3]上的图象；(2)根据函数图象写出函数f(x)的单调区间及最值．
解析：(1)画图如图：(2)根据函数图象，f(x)的单调递增区间为[－3，－2]，[0，2]，f(x)的单调递减区间为(－2，0)，(2，3]，f(x)的最大值为2，f(x)的最小值为－2.
学霸笔记：利用奇、偶函数的图象求解问题(1)依据：奇函数⇔图象关于原点对称，偶函数⇔图象关于y轴对称．(2)求解：根据奇、偶函数图象的对称性可以解决诸如求值、比较大小及解不等式问题．
跟踪训练2　已知奇函数f(x)定义域为[－5，5]且在[0，5]上的图象如图所示，求使f(x)<0的x的取值范围．
题型 3 利用函数的奇偶性求值例3　(1)已知f(x)＝x5＋ax3＋bx－8，若f(－3)＝10，则f(3)＝(　　)A．26 B．18C．10 D．－26
(2)将本例(2)中的函数改为函数f(x)＝x2－(2－m)x＋3为偶函数，则m的值是________．
解析：方法一　f(－x)＝(－x)2－(2－m)(－x)＋3＝x2＋(2－m)x＋3，由函数y＝f(x)为偶函数，知f(－x)＝f(x)，即x2＋(2－m)x＋3＝x2－(2－m)x＋3，∴2－m＝－(2－m)，∴m＝2.方法二　由f(－1)＝f(1)得4＋(2－m)＝4－(2－m)，解得m＝2.
题后师说1．利用函数奇偶性求值的方法(1)未知的值不在已知的范围内，可利用函数的奇偶性将未知的值或区间转化为已知的值或区间；(2)有些函数虽然是非奇非偶函数，但观察表达式可以发现其间存在奇偶性的表达式，所以可用奇函数或偶函数表达出此函数，从而间接地求值．
2．已知函数的奇偶性求参数的2种方法
跟踪训练3　(1)已知函数f(x)为R上的奇函数，当x<0时，f(x)＝x＋2，则f(0)＋f(3)＝(　　)A．－3 B．－1C．1 D．3
解析：因为函数f(x)为R上的奇函数，当x<0时，f(x)＝x＋2，所以f(3)＝－f(－3)＝－(－3＋2)＝1.而f(0)＝0，∴f(0)＋f(3)＝1.故选C.
随堂练习1.下列图象表示的函数中具有奇偶性的是(　　)
解析：选项A中的图象关于原点或y轴均不对称，故排除；选项C、D中的图象所示的函数的定义域不关于原点对称，不具有奇偶性，故排除；选项B中的图象关于y轴对称，其表示的函数是偶函数．故选B.
3．如图，给出奇函数y＝f(x)的局部图象，则2f(－1)＋3f(－2)的值为(　　)A．－7 B．7C．5 D．－5
4．若函数f(x)＝x3－bx2＋ax在[3a，2＋a]上为奇函数，则a＋b＝________．