高中数学湘教版（2019）必修 第二册4.2 平面习题

这是一份高中数学湘教版（2019）必修 第二册4.2 平面习题，共6页。

1．已知平面α∥平面β，a⊂α，b⊂β，则直线a，b的位置关系是( )
A．平行 B．相交
C．异面 D．平行或异面
2．两个平行平面与另两个平行平面相交得四条直线的位置关系是( )
A．两两相互平行
B．两两相交于同一点
C．两两相交但不一定交于同一点
D．两两相互平行或交于同一点
3．如图，已知平面α∥平面β，点P为α，β外一点，直线PB，PD分别与α，β相交于A，B和C，D，则AC与BD的位置关系为( )
A．平行 B．相交
C．异面 D．平行或异面
4．在长方体ABCD ­ A1B1C1D1中，若经过D1B的平面分别交AA1和CC1于点E，F，则四边形D1EBF的形状是( )
A．矩形 B．菱形
C．平行四边形 D．正方形
5．平面α∥平面β，点A，C在平面α内，点B，D在平面β内，若AB＝CD，则AB，CD的位置关系是( )
A．平行 B．相交
C．异面 D．以上都有可能
6．(多选)下列命题正确的是( )
A．平面α∥平面β，一条直线a平行于平面α，则a一定平行于平面β
B．平面α∥平面β，则平面α内的任意一条直线都平行于平面β
C．一个三角形有两条边所在的直线分别平行于一个平面，那么该三角形所在的平面与这个平面平行
D．分别在两个平行平面内的两条直线只能是平行直线或异面直线
7.
用一个平面去截三棱柱ABC­A1B1C1，交A1C1，B1C1，BC，AC分别于点E，F，G，H.若A1A>A1C1，则截面的形状可以为________．(把你认为可能的结果的序号填在横线上)
①一般的平行四边形；②矩形；③菱形；④正方形；⑤梯形．
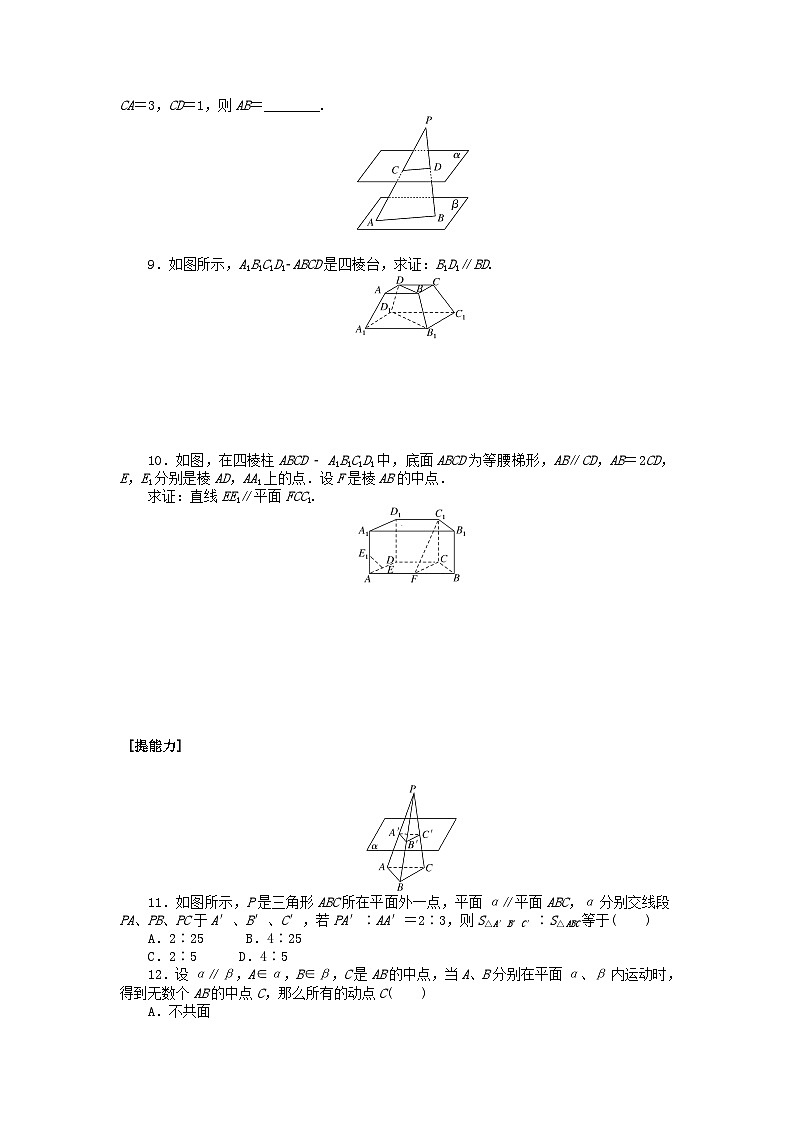
8．如图，平面α∥平面β，△PAB所在的平面与α，β分别交于CD，AB，若PC＝2，CA＝3，CD＝1，则AB＝________.
9．如图所示，A1B1C1D1­ABCD是四棱台，求证：B1D1∥BD.
10．如图，在四棱柱ABCD ­ A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB＝2CD，E，E1分别是棱AD，AA1上的点．设F是棱AB的中点．
求证：直线EE1∥平面FCC1.
[提能力]
11．如图所示，P是三角形ABC所在平面外一点，平面α∥平面ABC，α分别交线段PA、PB、PC于A′、B′、C′，若PA′∶AA′＝2∶3，则S△A′B′C′∶S△ABC等于( )
A．2∶25 B．4∶25
C．2∶5 D．4∶5
12．设α∥β，A∈α，B∈β，C是AB的中点，当A、B分别在平面α、β内运动时，得到无数个AB的中点C，那么所有的动点C( )
A．不共面
B．当且仅当A、B分别在两条直线上移动时才共面
C．当且仅当A、B分别在两条给定的异面直线上移动时才共面
D．不论A、B如何移动，都共面
13．正方体ABCD­A1B1C1D1的棱长为3，点E在A1B1上，且B1E＝1，平面α∥平面BC1E，若平面α∩平面AA1B1B＝A1F，则AF的长为________．
14．在正方体ABCD­A1B1C1D1中，AB＝4，M，N分别为棱A1D1，A1B1的中点，过点B的平面α∥平面AMN，则平面α截该正方体所得截面是________形，面积为________．
15．如图，在三棱柱ABC­A1B1C1中，E，F，G分别为B1C1，A1B1，AB的中点．若平面A1C1G∩BC＝H，求证：H为BC的中点．
[培优生]
16．如图，已知正方体ABCD­A1B1C1D1.
(1)求证：平面AB1D1∥平面C1BD；
(2)试找出体对角线A1C与平面AB1D1和平面C1BD的交点E，F，并证明A1E＝EF＝FC.
课时作业(三十八) 平面与平面平行的性质
1．解析：∵平面α∥平面β，∴平面α与平面β没有公共点．∵a⊂α，b⊂β，∴直线a，b没有公共点，∴直线a，b的位置关系是平行或异面．
答案：D
2．解析：根据平面与平面平行的性质可知，所得四条直线两两相互平行．
答案：A
3．解析：由题意知：P，A，B，C，D在同一平面内，且平面PBD∩平面α＝AC，平面PBD∩平面β＝BD，∵平面α∥平面β，∴AC∥BD.
答案：A
4．解析：如图，在长方体ABCDA1B1C1D1中，
平面ABB1A1∥平面CDD1C1，过D1B的平面BED1F与平面ABB1A1交于直线BE，与平面CDD1C1交于直线D1F.
由面面平行的性质定理，知BE∥D1F.
同理BF∥D1E.
所以四边形D1EBF为平行四边形．
答案：C
5．解析：可将AB与CD想象为同高圆台的母线，显然相交、平行、异面都有可能．
答案：D
6．解析：平面α∥平面β，一条直线a平行于平面α，则a可能在平面β内，故A错误；平面α∥平面β，则α内的任意一条直线都平行于平面β，故B正确；一个三角形有两条边所在的直线平行于一个平面，由面面平行的判定知，三角形所在的平面与这个平面平行，故C正确；分别在两个平行平面内的两条直线只能是平行直线或异面直线，不可能相交，故D正确．
答案：BCD
7．解析：当FG∥B1B时，四边形EFGH为矩形；当FG不与B1B平行时，四边形EFGH为梯形．
答案：②⑤
8．解析：∵平面α∥平面β，∴CD∥AB，则eq \f(PC,PA)＝eq \f(CD,AB)，
∴AB＝eq \f(PA×CD,PC)＝eq \f(5×1,2)＝eq \f(5,2).
答案：eq \f(5,2)
9．证明：根据棱台的定义可知，BB1与DD1相交，
所以BD与B1D1共面．
又因为平面ABCD∥平面A1B1C1D1，
且平面BB1D1D∩平面ABCD＝BD，
平面BB1D1D∩平面A1B1C1D1＝B1D1，
所以B1D1∥BD.
10．证明：因为F为AB的中点，所以AB＝2AF，
又因为AB＝2CD，所以CD＝AF，
因为AB∥CD，所以CD∥AF，所以AFCD为平行四边形，
所以FC∥AD，又FC⊄平面ADD1A1，
AD⊂平面ADD1A1所以FC∥平面ADD1A1，
因为CC1∥DD1，CC1⊄平面ADD1A1，
DD1⊂平面ADD1A1，
所以CC1∥平面ADD1A1，又FC∩CC1＝C，
所以平面ADD1A1∥平面FCC1.
又EE1⊂平面ADD1A1，所以EE1∥平面FCC1.
11．解析：∵平面α∥平面ABC，平面PAB与它们的交线分别为A′B′，AB，∴AB∥A′B′，
同理B′C′∥BC，易得△ABC∽△A′B′C′，
S△A′B′C′∶S△ABC＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(A′B′,AB)))eq \s\up12(2)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(PA′,PA)))eq \s\up12(2)＝eq \f(4,25).
答案：B
12．解析：
如图所示，A′、B′分别是A、B两点在α、β上运动后的两点，此时AB中点C变成A′B′的中点C′，连接A′B，取A′B的中点E.连接CE、C′E、AA′、BB′、CC′，则CE∥AA′，∴CE∥α.
又C′E∥BB′，∴C′E∥β.
又∵α∥β，∴C′E∥α.
∵C′E∩CE＝E，∴平面CC′E∥平面α，
∴CC′∥平面α.
∴不论A、B如何移动，所有的动点C都在过C点且与α、β平行的平面上．
答案：D
13．解析：因为平面α∥平面BC1E，平面α∩平面AA1B1B＝A1F，平面BC1E∩平面AA1B1B＝BE，所以A1F綊BE，
所以Rt△A1AF≌Rt△BB1E，
所以AF＝B1E＝1.
答案：1
14.
解析：如图所示，截面为等腰梯形BDPQ，且PQ＝2eq \r(2)，BD＝4eq \r(2)，等腰梯形的高为eq \r(（42＋22）－（\r(2)）2)＝3eq \r(2)，
故截面的面积为eq \f(1,2)×(2eq \r(2)＋4eq \r(2))×3eq \r(2)＝18.
答案：等腰梯 18
15．解析：∵E，F分别为B1C1，A1B1的中点，∴EF∥A1C1，
∵A1C1⊂平面A1C1G，EF⊄平面A1C1G，∴EF∥平面A1C1G，
又F，G分别为A1B1，AB的中点，∴A1F＝BG，
又A1F∥BG，∴四边形A1GBF为平行四边形，则BF∥A1G，
∵A1G⊂平面A1C1G，BF⊄平面A1C1G，∴BF∥平面A1C1G，
又EF∩BF＝F，EF，BF⊂面BEF，
∴平面A1C1G∥平面BEF；
∵平面ABC∥平面A1B1C1，
平面A1C1G∩平面A1B1C1＝A1C1，
平面A1C1G与平面ABC有公共点G，则有经过G的直线，设交BC于点H，
则A1C1∥GH，得GH∥AC，
∵G为AB的中点，∴H为BC的中点．
16．解析：(1)因为在正方体ABCDA1B1C1D1中，AD∥B1C1，
所以四边形AB1C1D是平行四边形，
所以AB1∥C1D，
又因为C1D⊂平面C1BD，AB1⊄平面C1BD，
所以AB1∥平面C1BD.
同理B1D1∥平面C1BD.
又因为AB1∩B1D1＝B1，AB1⊂平面AB1D1，B1D1⊂平面AB1D1，
所以平面AB1D1∥平面C1BD.
(2)如图，连接A1C1交B1D1于点O1，连接AO1与A1C交于点E.
又因为AO1⊂平面AB1D1，
所以点E也在平面AB1D1内，
所以点E就是A1C与平面AB1D1的交点．
连接AC交BD于点O，连接C1O，与A1C交于点F，则点F就是A1C与平面C1BD的交点．
下面证明A1E＝EF＝FC.
因为平面A1C1C∩平面AB1D1＝EO1，平面A1C1C∩平面C1BD＝C1F，而平面AB1D1∥平面C1BD，
所以EO1∥C1F.
在△A1C1F中，O1是A1C1的中点，
所以E是A1F的中点，即A1E＝EF.
同理可证OF∥AE，又因为O为AC的中点，
所以F是CE的中点，即CF＝FE.
因此A1E＝EF＝FC.