高中数学湘教版（2019）必修 第二册6.2 数学建模——从自然走向理性之路同步达标检测题

这是一份高中数学湘教版（2019）必修 第二册6.2 数学建模——从自然走向理性之路同步达标检测题，共6页。试卷主要包含了学校宿舍与办公室相距a m，有一支队伍长L m等内容，欢迎下载使用。


2．有一支队伍长L m．以速度v m/s匀速前进．排尾的传令兵因传达命令赶赴排头，到达排头后立即返回，往返速度不变．回答下列问题：
(1)如果传令兵行进的速度为整个队伍行进速度的2倍，求传令兵回到排尾时所走的路程；
(2)如果传令兵回到排尾时，全队正好前进了L m，求传令兵行走的路程．
课时作业(五十) 数学建模案例(一)：烧开水问题
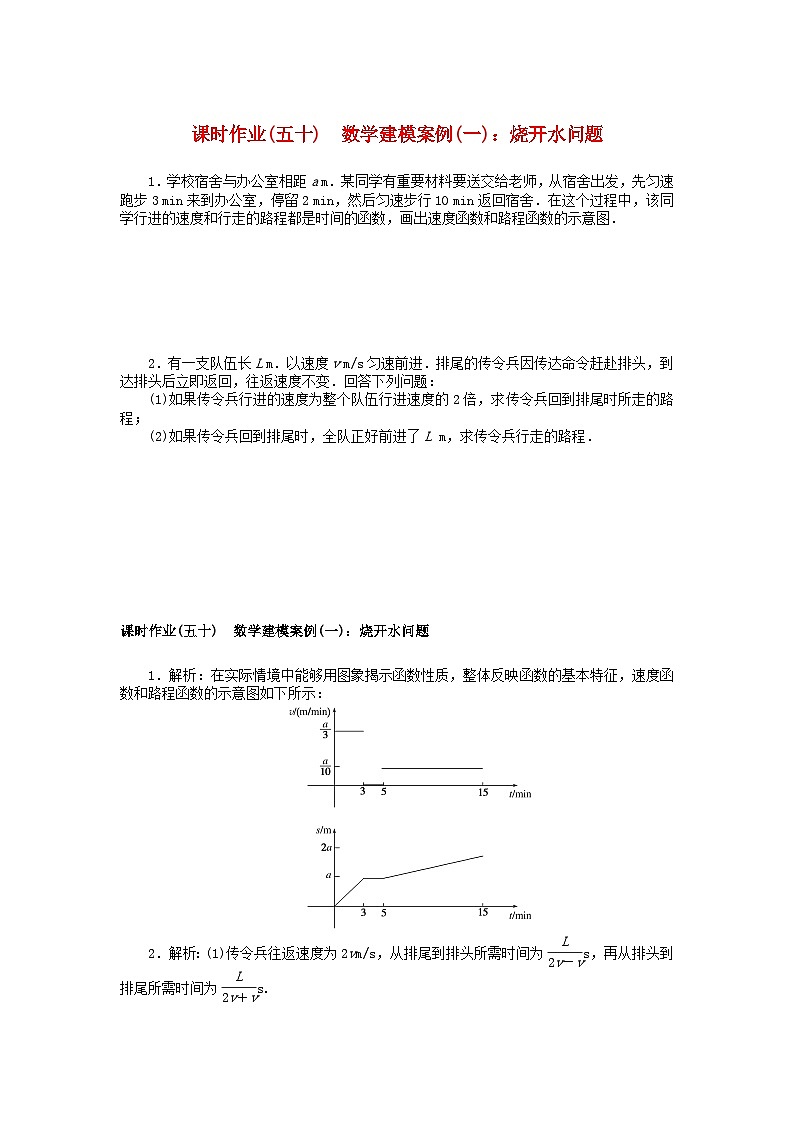
1．解析：在实际情境中能够用图象揭示函数性质，整体反映函数的基本特征，速度函数和路程函数的示意图如下所示：
2．解析：(1)传令兵往返速度为2vm/s，从排尾到排头所需时间为eq \f(L,2v－v)s，再从排头到排尾所需时间为eq \f(L,2v＋v)s.
故传令兵往返共用时间为eq \f(L,2v－v)＋eq \f(L,2v＋v)＝eq \f(4L,3v)(s)，
往返路程为2v×eq \f(4L,3v)＝eq \f(8,3)L(m).
(2)设传令兵的行进速度为v′，则传令兵从排尾到排头所需时间为eq \f(L,v′－v)s，再从排头到排尾所需时间为eq \f(L,v′＋v)s，往返共用时间t＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(L,v′－v)＋\f(L,v′＋v)))s，往返所走路程为v′tm．由传令兵回到排尾时全队正好前进了Lm，则L＝vt，故eq \f(L,v)＝eq \f(L,v′－v)＋eq \f(L,v′＋v)，解得v′＝(eq \r(2)＋1)v.
上式等号两边同乘t，得v′t＝(eq \r(2)＋1)vt＝(eq \r(2)＋1)L.
所以传令兵往返路程为(eq \r(2)＋1)Lm．