高中数学人教A版 (2019)必修 第一册4.2 指数函数当堂检测题

这是一份高中数学人教A版 (2019)必修 第一册4.2 指数函数当堂检测题，共10页。试卷主要包含了函数y＝2x＋1的图象是，故选B等内容，欢迎下载使用。


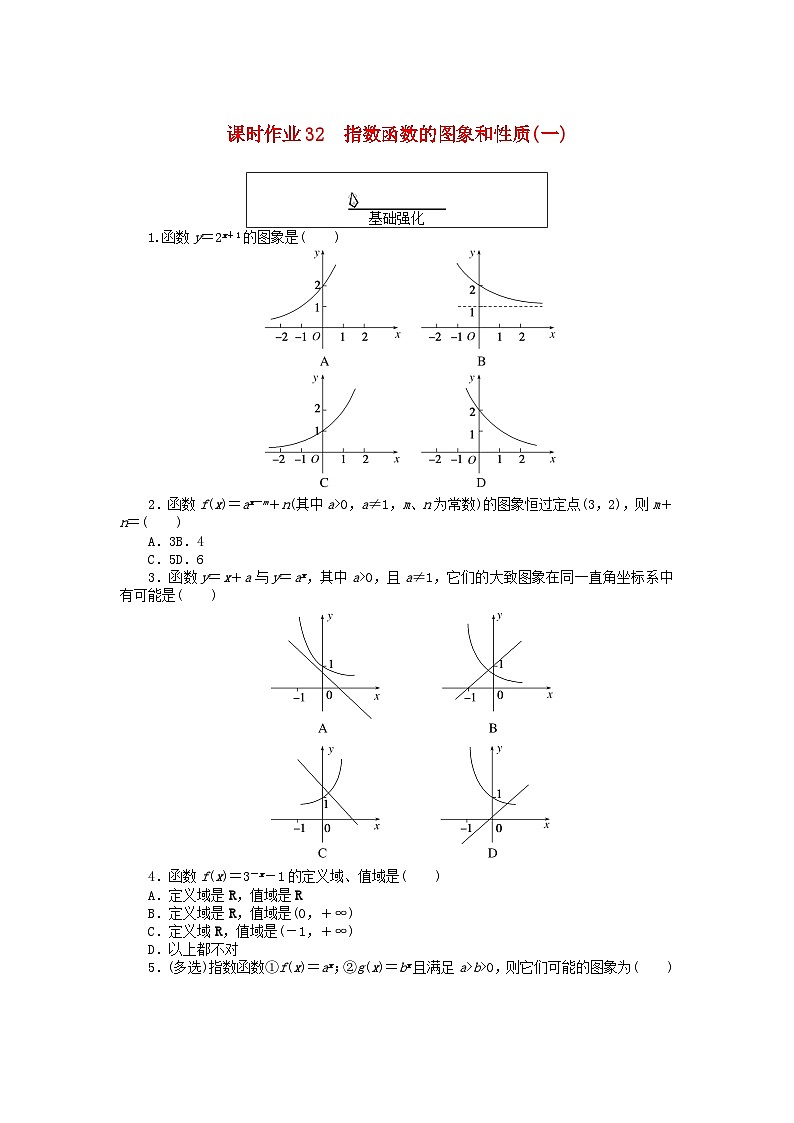
2．函数f(x)＝ax－m＋n(其中a>0，a≠1，m、n为常数)的图象恒过定点(3，2)，则m＋n＝( )
A．3B．4
C．5D．6
3．函数y＝x＋a与y＝ax，其中a>0，且a≠1，它们的大致图象在同一直角坐标系中有可能是( )
4．函数f(x)＝3－x－1的定义域、值域是( )
A．定义域是R，值域是R
B．定义域是R，值域是(0，＋∞)
C．定义域R，值域是(－1，＋∞)
D．以上都不对
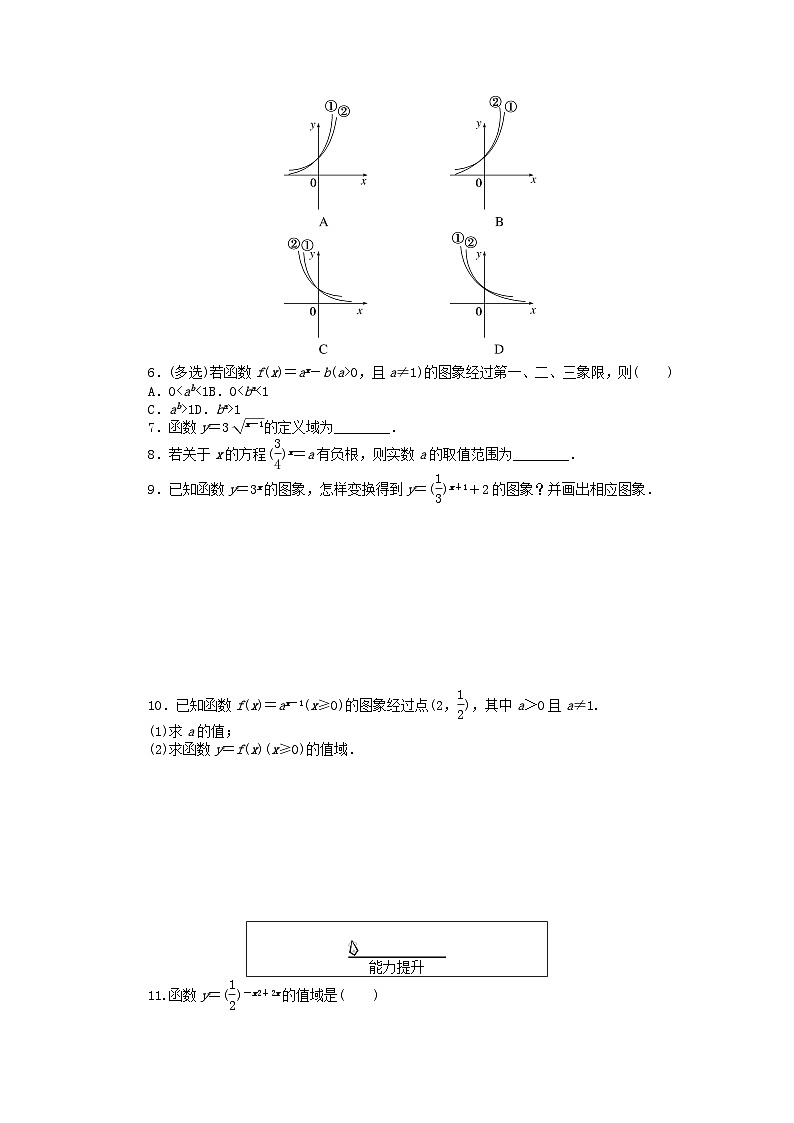
5．(多选)指数函数①f(x)＝ax；②g(x)＝bx且满足a>b>0，则它们可能的图象为( )
6．(多选)若函数f(x)＝ax－b(a>0，且a≠1)的图象经过第一、二、三象限，则( )
A．0C．ab>1D．ba>1
7．函数y＝3eq \r(x－1)的定义域为________．
8．若关于x的方程(eq \f(3,4))x＝a有负根，则实数a的取值范围为________．
9．已知函数y＝3x的图象，怎样变换得到y＝(eq \f(1,3))x＋1＋2的图象？并画出相应图象．
10．已知函数f(x)＝ax－1(x≥0)的图象经过点(2，eq \f(1,2))，其中a＞0且a≠1.
(1)求a的值；
(2)求函数y＝f(x)(x≥0)的值域．
11.函数y＝(eq \f(1,2))－x2＋2x的值域是( )
A．RB．[eq \f(1,2)，＋∞)
C．(2，＋∞) D．(0，＋∞)
12．已知函数f(x)＝ax＋b(a>0，a≠1)的定义域和值域都是[－1，0]，则a＋b＝( )
A．－eq \f(3,2)B．－1
C．1D．eq \f(3,2)
13．若函数f(x)＝(eq \f(1,3))|x|＋m－1的图象与x轴有公共点，则实数m的取值范围为( )
A．m<1B．m≤1
C．014．(多选)已知实数a，b满足等式2021a＝2022b，下列式子可以成立的是( )
A．a＝b＝0B．aC．015.已知函数f(x)＝a(eq \f(1,2))|x|＋b的图象过原点，且无限接近直线y＝1，但又不与该直线相交，则f(－2)＝________．
16．已知函数f(x)＝eq \b\lc\|\rc\|(\a\vs4\al\c1(（\f(1,2)）x－1)).
(1)画出函数f(x)的图象，并指出函数的单调区间；
(2)讨论直线y＝a与函数f(x)图象的交点个数．
课时作业32
1．解析：∵函数y＝2x＋1的图象是由函数y＝2x的图象向左平移1个单位长度得到的，而y＝2x的图象过定点(1，2)，∴y＝2x＋1的图象过点(0，2)，且在R上是增函数，故选A.
答案：A
2．解析：函数f(x)＝ax－m＋n(其中a>0，a≠1，m、n为常数)的图象恒过定点(3，2)，即2＝a3－m＋n恒成立，则有eq \b\lc\{(\a\vs4\al\c1(3－m＝0,1＋n＝2))，解得eq \b\lc\{(\a\vs4\al\c1(m＝3,n＝1))，所以m＋n＝4.故选B.
答案：B
3．解析：∵a>0，则y＝x＋a单调递增，故排除AC；对于BD，y＝ax单调递减，则0答案：D
4．解析：因为函数f(x)＝3－x－1＝(eq \f(1,3))x－1，所以其定义域为R，因为(eq \f(1,3))x>0，所以(eq \f(1,3))x－1>－1，所以函数的值域为(－1，＋∞)，故选C.
答案：C
5．解析：据指数函数图象性质，a>b>1时选A，1>a>b>0时选D，a>1>b时图象如图．
故选AD.
答案：AD
6．解析：因为函数f(x)＝ax－b(a>0，且a≠1)的图象经过第一、二、三象限，所以a>1，f(0)＝1－b∈(0，1)⇒0a0＝1，0答案：BC
7．解析：由x－1≥0，可得x≥1，所以函数y＝3eq \r(x－1)的定义域为[1，＋∞).
答案：[1，＋∞)
8．解析：关于x的方程(eq \f(3,4))x＝a有负根等价于指数函数y＝(eq \f(3,4))x与y＝a在第二象限有交点，则当a>1时，y＝(eq \f(3,4))x与y＝a在第二象限有交点，所以实数a的取值范围为(1，＋∞).
答案：(1，＋∞)
9．解析：y＝(eq \f(1,3))x＋1＋2＝3－(x＋1)＋2.作函数y＝3x的图象关于y轴的对称图象得函数y＝3－x的图象，再向左平移1个单位长度就得到函数y＝3－(x＋1)的图象，再后再向上平移2个单位长度就得到函数y＝3－(x＋1)＋2＝(eq \f(1,3))x＋1＋2的图象，如图所示．
10．解析：(1)∵f(x)的图象过点eq \b\lc\(\rc\)(\a\vs4\al\c1(2，\f(1,2)))，∴a2－1＝eq \f(1,2)，则a＝eq \f(1,2).
(2)由(1)知，f(x)＝(eq \f(1,2))x－1，x≥0.由x≥0，得x－1≥－1，于是0＜(eq \f(1,2))x－1≤(eq \f(1,2))－1＝2，所以函数y＝f(x)(x≥0)的值域为(0，2].
11．解析：令t＝－x2＋2x，则y＝(eq \f(1,2))t，且该函数为单调减函数，而t＝－x2＋2x＝－(x－1)2＋1≤1，所以y＝(eq \f(1,2))t≥eq \f(1,2)，即函数y＝(eq \f(1,2))－x2＋2x的值域是[eq \f(1,2)，＋∞)，故选B.
答案：B
12．解析：当a>1时，eq \b\lc\{(\a\vs4\al\c1(f（－1）＝a－1＋b＝－1,f（0）＝a0＋b＝0))，方程组无解，
当0∴a＋b＝eq \f(1,2)－2＝－eq \f(3,2).故选A.
答案：A
13．解析：∵|x|≥0，∴0<(eq \f(1,3))|x|≤1，∴m－1答案：D
14．解析：分别画出y＝2021x，y＝2022x的图象，如示意图：
实数a，b满足等式2021a＝2022b，可得：a>b>0，或a答案：ABD
15．解析：因为f(x)的图象过原点，所以f(0)＝a(eq \f(1,2))0＋b＝0，即a＋b＝0.又因为f(x)的图象无限接近直线y＝1，但又不与该直线相交，所以b＝1，a＝－1，
所以f(x)＝－(eq \f(1,2))|x|＋1，
所以f(－2)＝－(eq \f(1,2))2＋1＝eq \f(3,4).
答案：eq \f(3,4)
16．解析：(1)因为f(x)＝eq \b\lc\|\rc\|(\a\vs4\al\c1(（\f(1,2)）x－1))＝eq \b\lc\{(\a\vs4\al\c1(（\f(1,2)）x－1，x<0,1－（\f(1,2)）x，x≥0))，
画出其图象如下：
由图象可得，函数f(x)的单调递增区间为(0，＋∞)；单调递减区间为(－∞，0)；
(2)由(1)中图象可得，
当a<0时，直线y＝a与函数f(x)的图象没有交点；
当a＝0时，直线y＝a与函数f(x)的图象有一个交点；
当0当a≥1时，直线y＝a与函数f(x)的图象有一个交点；
综上，当a<0时，直线y＝a与函数f(x)图象的交点个数为0个；
当a＝0或a≥1时，直线y＝a与函数f(x)图象的交点个数为1个；
当0基础强化
能力提升