初中数学北师大版九年级下册5 三角函数的应用课堂检测

这是一份初中数学北师大版九年级下册5 三角函数的应用课堂检测，共3页。试卷主要包含了单选题，填空题，应用题，证明题等内容，欢迎下载使用。

一、单选题
1．数学活动小组到某广场测量标志性建筑AB的高度．如图，他们在地面上C点测得最高点A的仰角为22°，再向前70m至D点，又测得最高点A的仰角为58°，点C，D，B在同一直线上，则该建筑物AB的高度约为（ ）（精确到1m．参考数据：，，，）
A．28mB．34mC．37mD．46m
2．尚本步同学家住“3D魔幻城市”——重庆，他决定用所学知识测量自己居住的单元楼的高度．如图，小尚同学从单元楼CD的底端D点出发，沿直线步行42米到达E点，在沿坡度i=1：0.75的斜坡EF行走20米到达F点，最后沿直线步行30米到达隔壁大厦的底端B点，小尚从 B点乘直行电梯上行到顶端A点，从A点观测到单元顶楼C的仰角为28º，从点A观测到单元楼底端的俯角为37 º，若A、B、C、D、E、F在同一平面内，且D、E和F、B分别在通一水平线上，则单元楼CD的高度约为（ ）（结果精确到0.1米，参考数据：sin28 º≈0.47，cs28 º≈0.88，tan28 º≈0.53，sin37 º≈0.6，cs37 º≈0.8，tan37 º≈0.75）
A．79.0米B．107.5米C．112.6米D．123.5米
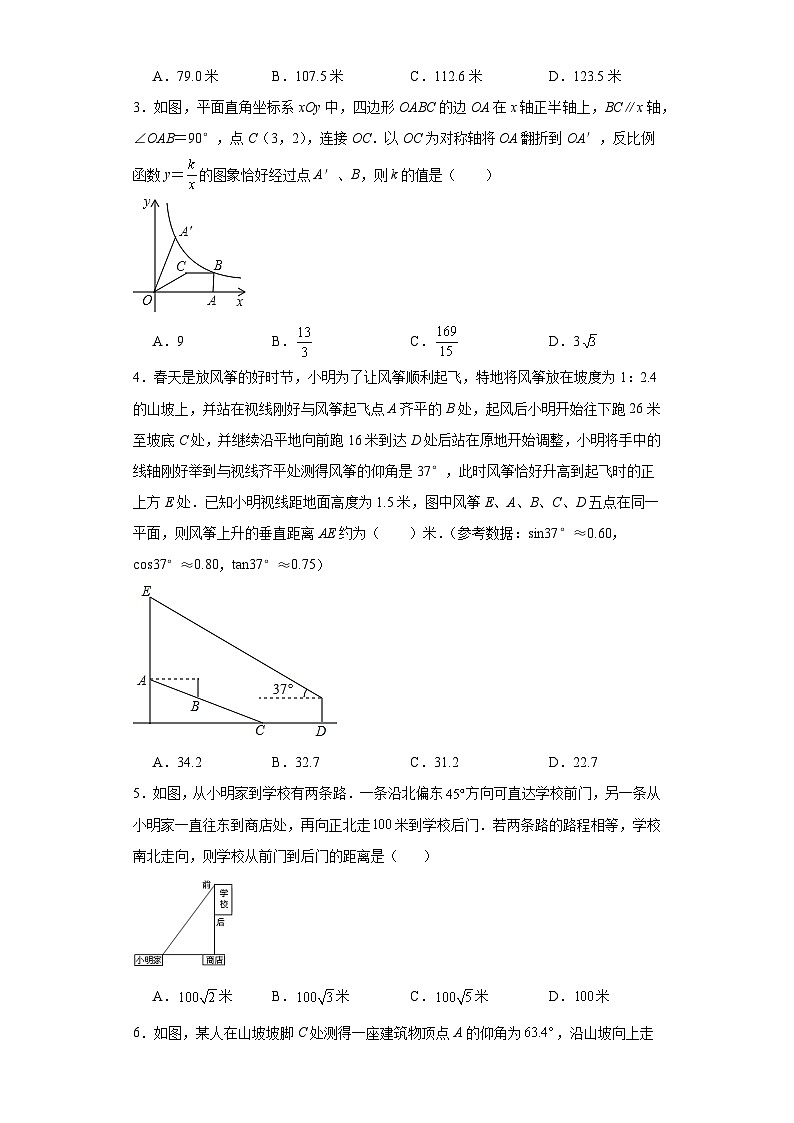
3．如图，平面直角坐标系xOy中，四边形OABC的边OA在x轴正半轴上，BC∥x轴，∠OAB＝90°，点C（3，2），连接OC．以OC为对称轴将OA翻折到OA′，反比例函数y＝的图象恰好经过点A′、B，则k的值是（ ）
A．9B．C．D．3
4．春天是放风筝的好时节，小明为了让风筝顺利起飞，特地将风筝放在坡度为1：2.4的山坡上，并站在视线刚好与风筝起飞点A齐平的B处，起风后小明开始往下跑26米至坡底C处，并继续沿平地向前跑16米到达D处后站在原地开始调整，小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°，此时风筝恰好升高到起飞时的正上方E处．已知小明视线距地面高度为1.5米，图中风筝E、A、B、C、D五点在同一平面，则风筝上升的垂直距离AE约为（ ）米．（参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75）
A．34.2B．32.7C．31.2D．22.7
5．如图，从小明家到学校有两条路．一条沿北偏东方向可直达学校前门，另一条从小明家一直往东到商店处，再向正北走米到学校后门．若两条路的路程相等，学校南北走向，则学校从前门到后门的距离是（ ）
A．米B．米C．米D．米
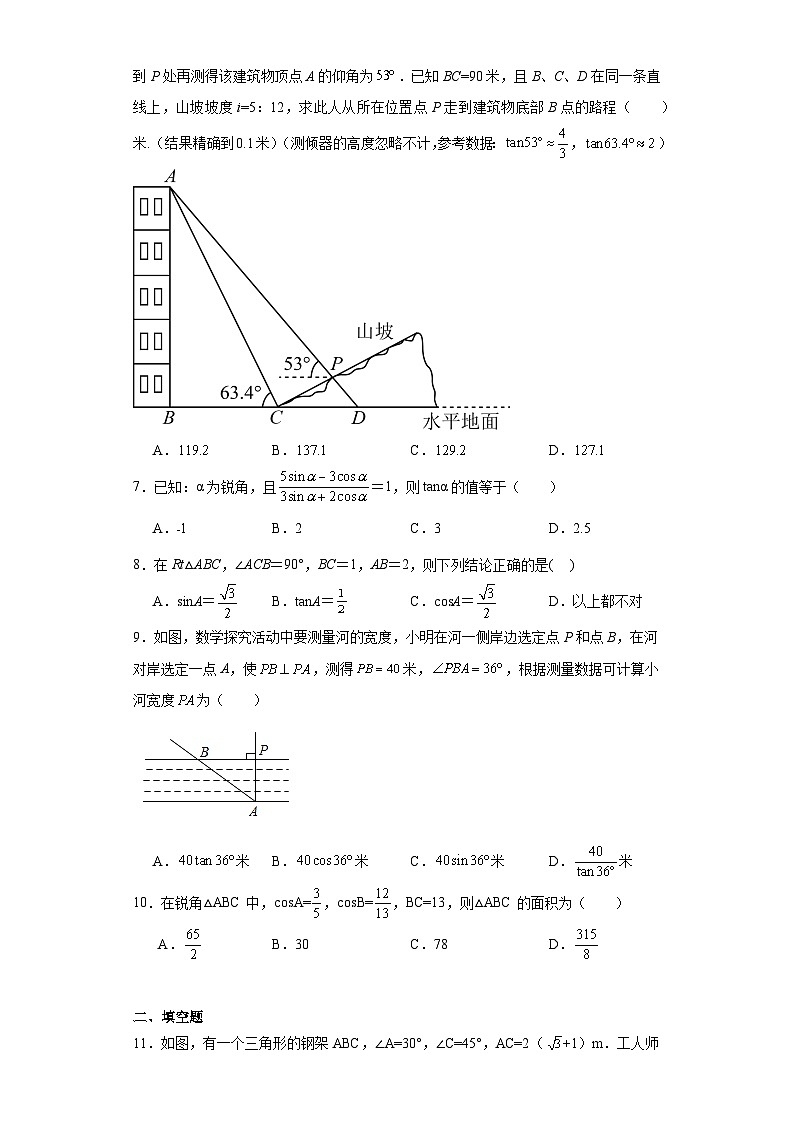
6．如图，某人在山坡坡脚C处测得一座建筑物顶点A的仰角为，沿山坡向上走到P处再测得该建筑物顶点A的仰角为．已知BC=90米，且B、C、D在同一条直线上，山坡坡度i=5：12，求此人从所在位置点P走到建筑物底部B点的路程（ ）米.（结果精确到0.1米）（测倾器的高度忽略不计，参考数据：，）
A．B．C．D．
7．已知：α为锐角，且＝1，则tanα的值等于（ ）
A．﹣1B．2C．3D．2.5
8．在Rt△ABC，∠ACB＝90°，BC＝1，AB＝2，则下列结论正确的是( )
A．sinA＝B．tanA＝C．csA＝D．以上都不对
9．如图，数学探究活动中要测量河的宽度，小明在河一侧岸边选定点P和点B，在河对岸选定一点A，使，测得米，，根据测量数据可计算小河宽度为（ ）
A．米B．米C．米D．米
10．在锐角△ABC中，csA=，csB=，BC=13，则△ABC的面积为（ ）
A．B．30C．78D．
二、填空题
11．如图，有一个三角形的钢架ABC，∠A=30°，∠C=45°，AC=2（+1）m．工人师傅搬运此钢架 （填“能”或“不能”）通过一个直径为2.1m的圆形门？
12．如图，高度相同的两根电线杆AB、CD均垂直于地面AF，某时刻电线杆AB的影子为地面上的线段AE，电线杆CD的影子为地面上的线段CF和坡面上的线段FG．已知坡面FG的坡比i=1：0.75，又AE=6米，CF=1米，FG=5米，那么电线杆AB的高度为 米．
13．如图，为了测量山的高度，先在山脚的一点测得山顶的仰角为，再沿坡角为的山坡走米到点，又测得山顶的仰角是，则山高 ．（带根号）
14．如图，是矗立在高速公路水平地面上的交通警示牌，经测量得到如下数据：AM=4米，AB=8米，∠MAD=45°，∠MBC=30°，则警示牌的高CD为 米（结果保留根号）．
15．如图，在中，，，，点，分别是边，上的动点，沿所在的直线折叠，使点的对应点始终落在边上，若为直角三角形，则的长为
16．从一艘船上测得海岸上高为米的灯塔项部的仰角是度，船离灯塔的水平距离为 ．
17．一艘观光游船从港口以北偏东的方向出港观光，航行海里至处时发生了侧翻沉船事故．一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东方向，马上以海里每小时的速度前往救援．海警船大约需 小时到达事故船处，()
18．“湾区之光”摩天轮位于深圳市华侨城欢乐港湾内，是深圳地标性建筑之一．摩天轮采用了世界首创的鱼鳍状异形大立架，有28个进口轿厢，每个轿厢可容纳25人．小亮在轿厢B处看摩天轮的圆心O处的仰角为30°，看地面A处的俯角为45°（如图所示，垂直于地面），若摩天轮的半径为54米，则此时小亮到地面的距离为 米．（结果保留根号）
19．在中，，，，则的周长为 ．
20．如图，从热气球C处测得地面A，B两点的俯角分别为30°，45°，如果此时热气球C处的高度CD为100 m，A，D，B三点在同一直线上，则A，B两点间的距离是 m．
三、应用题
21．如图是某景区登山路线示意图，其中是车游览路线，折线是登山步道，步道与水平面的夹角为，步道与水平面的夹角为是半山观景平台，．现测得，缆车路线．其中A，B，C，D，E在同一平面内，．
(1)填空：_________度，_________度；
(2)求点B到水平面的距离；
(3)求半山观景平台的长度．（结果保留根号）
22．如图，小明在家乡的楼顶上A处测得池塘的一端B处的俯角为，测得池塘D处的俯角，B、D、C三点在同一水平直线上，已知楼高米，求池塘宽为多少米？（参考数据：．结果保留一位小数．）
23．某地为创建特色小城，决定在辖区的一条河上修建一座步行观光桥．如图，该河旁有一座小山，山高，从山顶B处测得河岸A和对岸E的俯角分别，，点C、与河岸A、E在同一水平线上．
(1)求坡面的长度；（精确到）
(2)若在此处建桥，试求河宽的长度．（精确到0.1）（参考数据：，，，）
24．在某两个时刻，太阳光线与地面的夹角分别为和，树长．
(1)如图①，若树与地面的夹角为，则两次影长的和 ；
(2)如图②，若树与地面的夹角为，求两次影长的和（用含的式子表示）．
（参考数据：，，
25．为了方便观测动物的活动情况，某湿地公园要铺设一段道路．计划从图中，两处分别向处铺设，现测得，，，求，两点间的距离．（结果取整数，参考数据：，，）

四、证明题
26．如图，已知，在的角平分线上有一点，将一个角的顶点与点重合，它的两条边分别与射线相交于点.
（1）如图1，当绕点旋转到与垂直时，请猜想与的数量关系，并说明理由；
（2）当绕点旋转到与不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；
（3）如图3，当绕点旋转到点位于的反向延长线上时，求线段与之间又有怎样的数量关系？请写出你的猜想，不需证明.
27．定义：如果一个三角形中有两个内角α，β满足α+2β＝90°，那我们称这个三角形为“近直角三角形”．
（1）若△ABC是“近直角三角形”，∠B＞90°，∠C＝50°，则∠A＝ 度；
（2）如图1，在Rt△ABC中，∠BAC＝90°，AB＝3，AC＝4．若BD是∠ABC的平分线，
①求证：△BDC是“近直角三角形”；
②在边AC上是否存在点E（异于点D），使得△BCE也是“近直角三角形”？若存在，请求出CE的长；若不存在，请说明理由．
（3）如图2，在Rt△ABC中，∠BAC＝90°，点D为AC边上一点，以BD为直径的圆交BC于点E，连结AE交BD于点F，若△BCD为“近直角三角形”，且AB＝5，AF＝3，求tan∠C的值．
参考答案：
1．C
2．B
3．C
4．D
5．A
6．D
7．D
8．C
9．A
10．D
11．能
12．
13．
14．一4
15．或
16．米
17．
18．
19．
20．
21．(1)，
(2)
(3)
22．池塘宽为127.3米
23．(1)坡面的长度为
(2)河宽的长度为
24．(1)14
(2)米
25．
26．（1）（2）结论仍然成立（3）
27．（1）20；（2）①略；②存在，CE＝；（3）tan∠C的值为或．