湖南省张家界市慈利县2021-2022学年八年级下学期期末考试数学试题

这是一份湖南省张家界市慈利县2021-2022学年八年级下学期期末考试数学试题，共4页。试卷主要包含了选择题，填空题，解答下列各题等内容，欢迎下载使用。
考生注意：全卷共有三道大题，满分100分，时量120分钟。
一、选择题（每小题3分，共8道小题，合计24分）
1．下列图形中，既是中心对称图形也是轴对称图形的是（ ）
A．B．C．D．
2．如图，CD是Rt△ABC斜边AB上的中线，∠ACB＝90°，
∠CDB＝100°，则∠A等于（ ）
A．20°B．45°C．50°D．80°
3．如图，在矩形ABCD中，AC、BD相交于点O，若AB＝6， 第2题图
AO＝5，则矩形ABCD的面积为（ ）
A．24B．30C．48D．60
4．下列命题是真命题的是（ ）
A．有一组对边平行，另一组对边相等的四边形是平行四边形
B．两条对角线相等的四边形是矩形 第3题图
C．一条对角线平分一组对角的四边形是菱形
D．对角线互相垂直平分且相等的四边形是正方形
5．将点P（-5，4）向右平移4个单位，向上平移2个单位，得到点P的对应点P '的坐标是（ ）
A．（-1，6）B．（-1，2）C．（-5，6）D．（-9，6）
6．在同一坐标系中，函数y＝kx与y＝x﹣k的图象大致是（ ）
A． B． C． D．
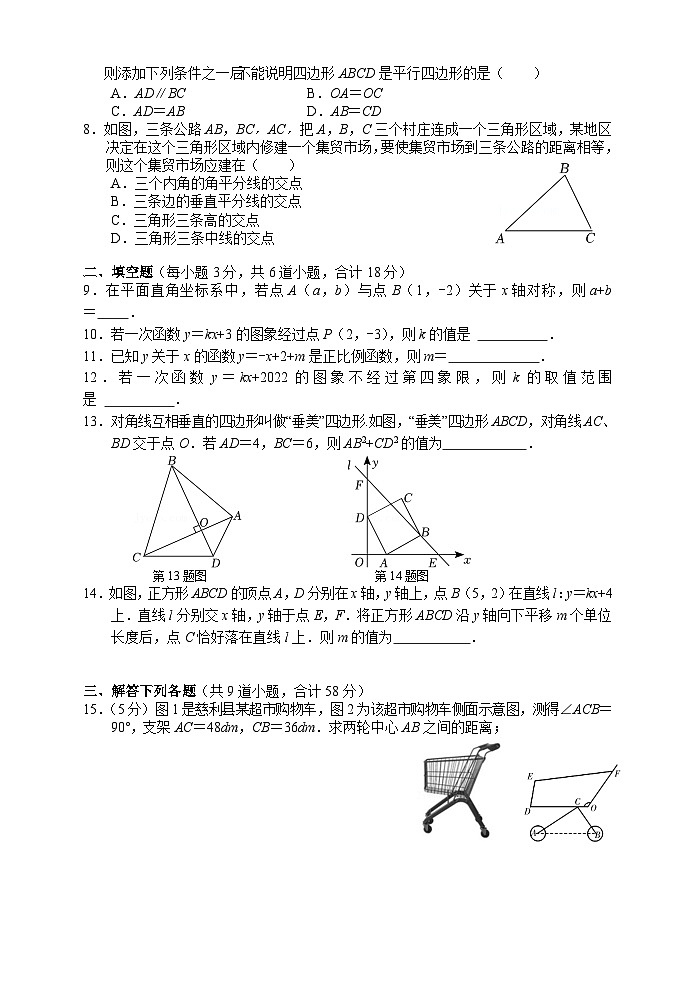
7．如图，在四边形ABCD中，若AB∥CD，AC交BD于点O，则添加下列条件之一后不能说明四边形ABCD是平行四边形的是（ ）
A．AD∥BCB．OA＝OC
C．AD＝ABD．AB＝CD
8．如图，三条公路AB，BC，AC，把A，B，C三个村庄连成一个三角形区域，某地区决定在这个三角形区域内修建一个集贸市场，要使集贸市场到三条公路的距离相等，则这个集贸市场应建在（ ）
A．三个内角的角平分线的交点
B．三条边的垂直平分线的交点
C．三角形三条高的交点
D．三角形三条中线的交点
二、填空题（每小题3分，共6道小题，合计18分）
9．在平面直角坐标系中，若点A（a，b）与点B（1，-2）关于x轴对称，则a+b＝ ．
10．若一次函数y＝kx+3的图象经过点P（2，-3），则k的值是 ．
11．已知y关于x的函数y＝-x+2+m是正比例函数，则m＝ ．
12．若一次函数y＝kx+2022的图象不经过第四象限，则k的取值范围是 ．
13．对角线互相垂直的四边形叫做“垂美”四边形.如图，“垂美”四边形ABCD，对角线AC、BD交于点O．若AD＝4，BC＝6，则AB2+CD2的值为 ．

第13题图 第14题图
14．如图，正方形ABCD的顶点A，D分别在x轴，y轴上，点B（5，2）在直线l：y＝kx+4上．直线l分别交x轴，y轴于点E，F．将正方形ABCD沿y轴向下平移m个单位长度后，点C恰好落在直线l上．则m的值为 ．
三、解答下列各题（共9道小题，合计58分）
15．（5分）图1是慈利县某超市购物车，图2为该超市购物车侧面示意图，测得∠ACB＝90°，支架AC＝48dm，CB＝36dm．求两轮中心AB之间的距离；
16．（5分）如图，已知∠AOB＝30°，P是∠AOB的平分线OC上的任意一点，PD∥OA交OB于点D，PE⊥OA于点E，如果OD＝10cm，求PE的长．
17．（6分）已知关于x的一次函数表达式是y＝（1-3k）x+2k-1．
（1）当k为何值时，函数图象过原点？
（2）若y随x的增大而增大，求k的取值范围．
18．（6分）已知：如图，在等腰△ABC中，AB＝BC，BO平分∠ABC交AC于点O，延长BO至点D，使OD＝BO，连接AD，CD，过点D作DE⊥BD交BC的延长线于点E．
（1）求证：四边形ABCD是菱形；
（2）如果AB＝2，∠BAD＝60°，求DE的长．
19．（6分）如图，一次函数y＝-2x+4的图象分别与x轴、y轴交于点A，B．
（1）求△AOB的面积；
（2）在该一次函数图象上有一动点P到x轴的距离为6，求点P的坐标．
20．（6分）小明用充电器给某手机充电时，发现其屏幕画面显示目前电量为20%（如图1）．经测试，在用快速充电器和普通充电器对该手机充电时，其电量y（单位：%）与充电时间x（单位：h）的函数图象分别为图2中的线段AB、AC．根据以上信息，回答下列问题：
（1）在目前电量20%的情况下，用充电器给该手机充满电时，快速充电器比普通充电器少用 小时．
（2）求线段AB对应的函数表达式；

21．（6分）在平面直角坐标系中，对于A（x1，y1）、B（x2，y2）两点，用以下方式定义两点间的“极大距离”d（A，B）；若，则d（A，B）＝；若，则d（A，B）＝．
例如：如图，点P（2，3），则d（P，O）＝3．
（1）若点A（3，2）、B（-1，-1），则d（A，B）＝ ．
（2）点C（-1，2）到坐标原点O的“极大距离”是 ．
（3）已知点M（a，a），d（M，O）＝2，O为坐标原点，求a的值．
22．（8分）“每天锻炼一小时，健康工作五十年，幸福生活一辈子”．为增强学生的身体素质，教育行政部门规定学生每天参加户外活动的平均时间不少于1小时．为了了解学生参加户外活动的情况，某校对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制作成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次调查中共调查了多少名学生？
（2）求户外活动时间为1.5小时的人数，并补充频数分布直方图；
（3）求表示户外活动时间1小时的扇形圆心角的度数；
（4）本次调查中学生参加户外活动的平均时间是否符合要求？(说明理由)
23．（10分）如图，平面直角坐标系中，O是坐标原点，直线y＝kx+8（k≠0）经过点C（2，4），与x轴交于点A，与y轴交于点B．线段CD平行于x轴，交直线于点D．连接OC、AD．
（1）求直线AB的解析式；
（2）求证：四边形OCDA是平行四边形；
（3）点P为直线AC上一点，连接OP、PD，当S△POD＝2S△COD，求此时点P的坐标；
题 号
一
二
三
总 分
得 分
题 号
1
2
3
4
5
6
7
8
答 案
二○二二年春季期末教学质量检测
八年级数学参考答案
一、选择题（每小题3分，共8道小题，合计24分）
二、填空题（每小题3分，共6道小题，合计18分）
9．3 10．-3 11．-2 12．k＞0 13．52 14．
三、解答下列各题（共9道小题，58分）
15．（dm）
16．PE＝5cm
17．（1）当k＝0.5时，图象过原点； （2）k的取值范围是k＜．
18．（1）证明：∵AB＝BC，BO平分∠ABC，∴BD⊥AC，AO＝CO，
∵BO＝DO，∴四边形ABCD是平行四边形，∵BD⊥AC，∴四边形ABCD是菱形；
（2）解：∵四边形ABCD是菱形，∴AC⊥BD，AC平分∠BAD，∠ABD＝∠CBD，
∴∠BOC＝∠AOB＝90°，∵∠BAD＝60°，∴∠BAC＝∠BAD＝30°，
∵AB＝2，BO＝DO，∴BO＝DO＝AB＝1，即BD＝1+1＝2，
∵∠AOB＝90°，∠BAC＝30°，∴∠ABO＝60°，∴∠DBC＝∠ABD＝60°，
∵DE⊥BD，∴∠BDE＝90°，
∴∠E＝30°，∴BE＝2BD＝4，
由勾股定理得：．
19．（1）∵A（2，0），B（0，4）AO＝2，BO＝4∴S△AOB＝AO×BO＝4
（2）∵点P到x轴的距离为6∴点P的纵坐标为±6∴P点坐标（-1，6），（5，-6）
20．（1）由图象可知，充满电时，快速充电器比普通充电器少用6-2＝4（小时），
（2）设线段AB对应的函数表达式为y＝kx+b，将（0，20），（2，100）代入得：
，解得，
∴线段AB对应的函数表达式为y＝40x+20，（0≤x≤2）；
21．（1）∵A（3，2）、B（-1，-1），∴|x1-x2＝4，|y1-y2|＝3，∴d（A，B）＝4，
（2）2
（3）当a＞0时，，∴a＝；当a＜0时，，∴；
综上所述：a的值为或；
22．（1）＝50（名），答：在这次调查中共调查了50名学生；
（2）户外活动时间为1.5小时的人数是：50×24%＝12（人），
（3）户外活动时间1小时的扇形圆心角的度数为×360°＝144°；
（4）本次调查中学生参加户外活动的平均时间是:
＝1.18＞1，
∴本次调查中学生参加户外活动的平均时间符合要求．
23．（1）将C（2，4）代入y＝kx+8，得k＝﹣2，
∴直线AB的解析式为y＝﹣2x+8．（3分）
（2）当y＝0时代入y＝﹣2x+8，得x＝4，即点A（4，0），
∴OA＝4．∵CD平行于x轴，则点D的纵坐标为4，
∴将y＝4代入y＝，得x＝6．∴点D（6，4），C（2，4）．∴CD＝4．
∴OA＝CD，且OA∥CD．∴四边形OCDA是平行四边形．（3分）
（3）∵△POD与△COD的底都是OD，
∴当S△POD＝2S△COD 时，则点P到OD的距离是点C到OD距离的2倍，
如图2，设将直线OD向上平移b（b＞0）个单位得到直线l1，使得直线l1经过点C，
∴直线l1的解析式为y＝+b，经过点C（2，4），则可得．
∵点P到OD的距离是点C到OD距离的2倍，
①将直线OD向上平移2b（b＞0）个单位得到直线l2，
∴直线l2的解析式为．∴直线l2与直线AC的交点即为点P，
∴，解得，∴点P的坐标为（1，6）；
②将直线OD向上平移2b（b＞0）个单位得到直线l3，
∴直线l3的解析式为．∴直线l3与直线AC的交点即为点P，
∴，解得，∴点P的坐标为（5，-2）．
综上所述点P的坐标：（1，6）或（5，-2） （4分）
题号
1
2
3
4
5
6
7
8
答案
D
C
C
D
A
B
C
A