人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式说课ppt课件

这是一份人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式说课ppt课件，共22页。PPT课件主要包含了共学案，答案A，答案D，答案C，x－2x3等内容，欢迎下载使用。

【学习目标】　(1)会将简单的分式不等式化为一元二次不等式求解．(2)理解一元二次方程，一元二次不等式与二次函数的关系．(3)能够从实际生活和生产中抽象出一元二次不等式的模型，解决实际生活问题．
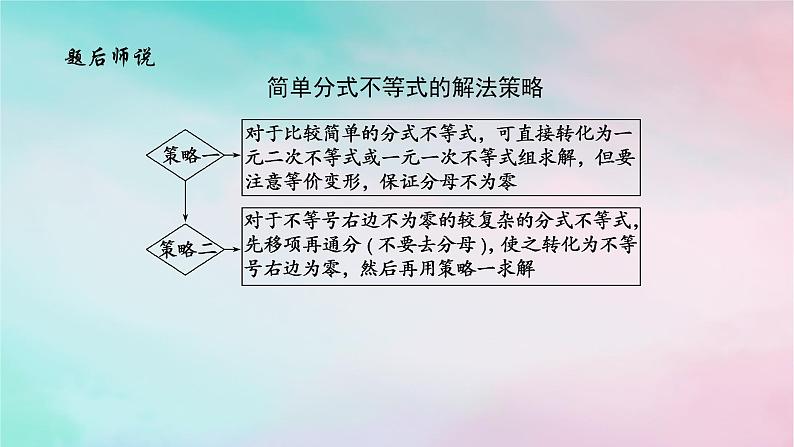
题后师说简单分式不等式的解法策略
题型 2 一元二次不等式的实际应用例2　某公司为了竞标某活动的相关代言，决定对旗下的某商品进行一次评估．该商品原来每件售价为25元，年销售8万件．据市场调查，若价格每提高1元，销售量将相应减少2 000件，要使销售的总收入不低于原收入，该商品每件定价最多为多少元？
题后师说求解一元二次不等式应用问题的步骤
跟踪训练2　制作一个高为20 cm的长方体容器，底面矩形的长比宽多10 cm，并且容积不少于4 000 cm3.问：底面矩形的宽至少应是多少？
解析：设底面矩形的宽为x，由题意可得20x(x＋10)≥4 000，整理可得x2＋10x－200≥0，解得x≤－20(舍)，或x≥10，所以底面矩形的宽至少为10 cm.
题型 3 二次函数与一元二次方程、不等式间的关系及应用例3　已知关于x的不等式ax2＋bx＋c＞0的解集为{x|2＜x＜3}，求关于x的不等式cx2＋bx＋a＜0的解集． 
一题多变　将本例中的“不等式ax2＋bx＋c＞0的解集为{x|2＜x＜3}”改为“不等式ax2＋bx＋c＞0的解集为{x|x<2或x>3}”，求关于x的不等式cx2＋bx＋a＜0的解集．
学霸笔记已知以a，b，c为参数的不等式(如ax2＋bx＋c>0)的解集，求解其他不等式的解集时，一般遵循：(1)根据解集来判断二次项系数的符号；(2)根据根与系数的关系把b，c用a表示出来并代入所要解的不等式；(3)约去a，将不等式化为具体的一元二次不等式求解．
2．已知关于x的不等式2x2－mx＋n<0的解集是(2，3)，则m＋n的值是(　　)A．－2 B．2C．22 D．－22
3．某村办服装厂生产某种风衣，月销售量x(件)与售价p(元/件)的关系为p＝300－2x；生产x件的成本r＝500＋30x(元)，为使月获利不少于8 600元，则月产量x满足(　　)A．55≤x≤60 B．60≤x≤65C．65≤x≤70 D．70≤x≤75
解析：由题意可得(300－2x)x－(500＋30x)≥8 600，即x2－135x＋4 550≤0，则(x－65)(x－70)≤0，故65≤x≤70.故选C.
4．已知不等式ax2－x＋6>0的解集为{x|－3

相关课件

人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式课文ppt课件： 这是一份人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式课文ppt课件，共38页。PPT课件主要包含了a＝b，预习自测，答案B等内容，欢迎下载使用。

高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式教学演示ppt课件： 这是一份高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.3 二次函数与一元二次方程、不等式教学演示ppt课件，共33页。PPT课件主要包含了素养·目标定位，课前·基础认知，课堂·重难突破，随堂训练，一解分式不等式，典例剖析等内容，欢迎下载使用。

人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式多媒体教学课件ppt： 这是一份人教A版 (2019)必修 第一册2.3 二次函数与一元二次方程、不等式多媒体教学课件ppt，共11页。PPT课件主要包含了-1a4，-3k0，m≥6等内容，欢迎下载使用。