高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示同步测试题

这是一份高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示同步测试题，共4页。

A．f：x→y＝xB．f：x→y＝x2
C．f：x→y＝2xD．f：x→y＝2x＋2
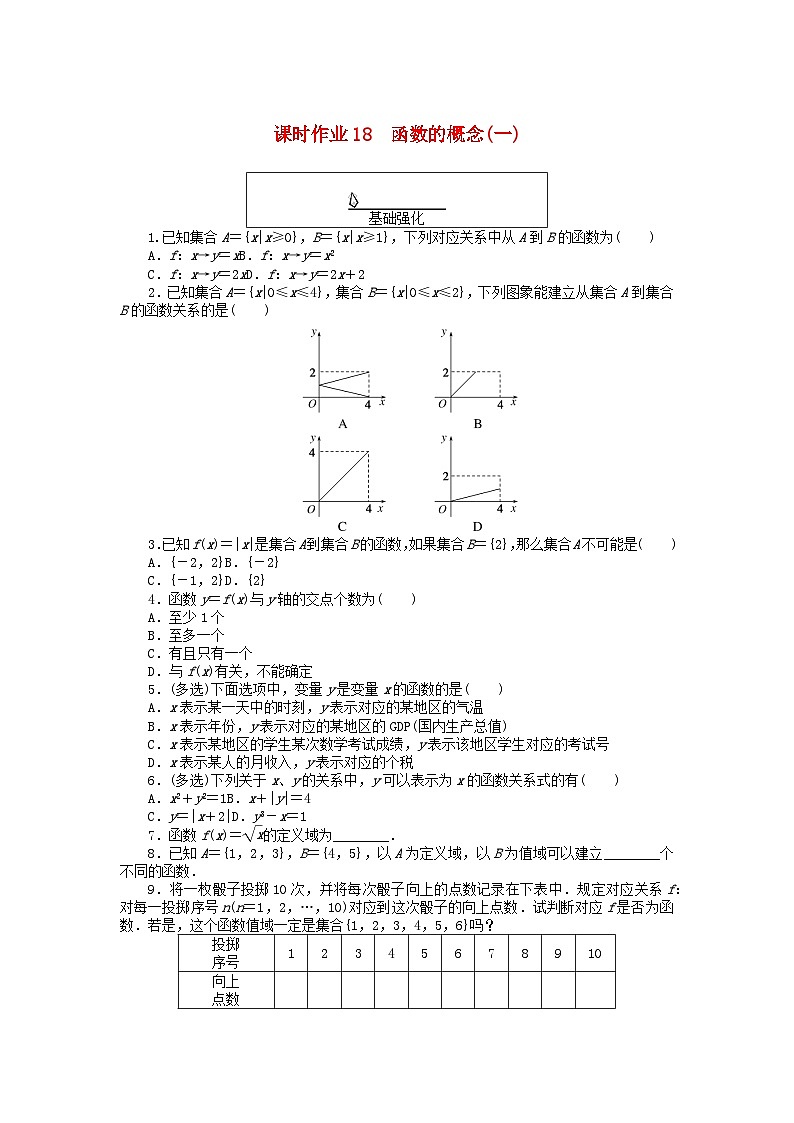
2．已知集合A＝{x|0≤x≤4}，集合B＝{x|0≤x≤2}，下列图象能建立从集合A到集合B的函数关系的是( )
3．已知f(x)＝|x|是集合A到集合B的函数，如果集合B＝{2}，那么集合A不可能是( )
A．{－2，2}B．{－2}
C．{－1，2}D．{2}
4．函数y＝f(x)与y轴的交点个数为( )
A．至少1个
B．至多一个
C．有且只有一个
D．与f(x)有关，不能确定
5．(多选)下面选项中，变量y是变量x的函数的是( )
A．x表示某一天中的时刻，y表示对应的某地区的气温
B．x表示年份，y表示对应的某地区的GDP(国内生产总值)
C．x表示某地区的学生某次数学考试成绩，y表示该地区学生对应的考试号
D．x表示某人的月收入，y表示对应的个税
6．(多选)下列关于x、y的关系中，y可以表示为x的函数关系式的有( )
A．x2＋y2＝1B．x＋|y|＝4
C．y＝|x＋2|D．y3－x＝1
7．函数f(x)＝eq \r(x)的定义域为________．
8．已知A＝{1，2，3}，B＝{4，5}，以A为定义域，以B为值域可以建立________个不同的函数．
9．将一枚骰子投掷10次，并将每次骰子向上的点数记录在下表中．规定对应关系f：对每一投掷序号n(n＝1，2，…，10)对应到这次骰子的向上点数．试判断对应f是否为函数．若是，这个函数值域一定是集合{1，2，3，4，5，6}吗？
10．求下列函数的定义域：
(1)f(x)＝eq \f(1,x2－1)；
(2)f(x)＝eq \r(2＋x)＋eq \r(1－x)；
(3)f(x)＝eq \f(\r(x＋1),x＋2).
11.如图所示某加油站地下圆柱体储油罐示意图，已知储油罐长度为d，截面半径为r(d，r为常量)，油面高度为h，油面宽度为w，油量为v(h，w，v为变量)，则下列说法错误的是( )
A．w是v的函数B．v是w的函数
C．h是v的函数D．v是h的函数
12．已知集合A＝{1，2，k}，B＝{4，7，10}，x∈A，y∈B，使B中元素y和A中元素x一一对应，对应关系为y＝3x＋1，则k的值为( )
A．2B．3
C．4D．5
13．已知A＝{a，b，c}(a，b，c∈R)，B＝{－1，0，1}，在f：A→B的函数中，满足f(a)＋f(b)＝f(c)的函数个数共有( )个
A．8B．6
C．9D．7
14．(多选)记无理数π＝3.1415926…0288…小数点后第a位上的数字是b，则b是a的函数，记作b＝f(a)，定义域为A，值域为B，下列说法正确的是( )
A．值域B是定义域A的子集
B．函数图象f(a)是一群孤立的点
C．f(6)＝2
D．a也是b的函数，记作a＝f(b)
15.函数f(x)＝eq \r(－mx2－2x＋1)的定义域为R，则实数m的取值范围是________．
16．试构建一个问题情境，使其中的变量关系可以用解析式y＝eq \f(10,x)(x∈{x|x＞0})来描述．
课时作业18
1．解析：对于A，在对应关系f：x→y＝x中，当x＝0时，y＝0，则集合B中没有元素和x对应，不是从集合A到集合B的函数，故A错误，
对于B，在对应关系f：x→y＝x2中，当x＝0时，y＝0，则集合B中没有元素和x对应，不是从集合A到集合B的函数，故B错误，
对于C，在对应关系f：x→y＝2x中，当x＝0时，y＝0，则集合B中没有元素和x对应，不是从集合A到集合B的函数，故C错误，
对于D，在对应关系f：x→y＝2x＋2中，因为x≥0，所以y∈{x|x≥2}{x|x≥1}，则集合A中任意一个元素x在集合B中都有唯一的元素与之对应，满足函数的定义，是从集合A到集合B的函数，故D正确．故选D.
答案：D
2．解析：对选项A：存在点使一个x与两个y对应，不符合，排除；
对选项B：当2对选项C：y的范围超出了集合B的范围，不符合，排除；
对选项D：满足函数关系的条件，正确．故选D.
答案：D
3．解析：若集合A＝{－1，2}，则－1∈A，但|－1|＝1∉B.故选C.
答案：C
4．解析：由函数定义可知，定义域包含x＝0时，则与y轴有1个交点，当定义域不包含x＝0时，则与y轴无交点，所以函数y＝f(x)与y轴的交点个数为0个．故选B.
答案：B
5．解析：ABD均满足函数的定义，C选项，同一个分数可以对应多个考试号，不满足对于任意的x，都有唯一的y与其对应，故C选项错误．故选ABD.
答案：ABD
6．解析：根据函数的定义，函数关系中任意一个x都有唯一的y对应，可看出：选项A，B的关于x、y的关系式中一个x都有两个y与之对应，不能构成函数关系；选项C，D中的任意一个x都有唯一的y对应，能构成函数关系．故选CD.
答案：CD
7．解析：要使函数f(x)＝eq \r(x)有意义，只需x≥0.
所以函数f(x)＝eq \r(x)的定义域为{x|x≥0}．
答案：{x|x≥0}
8．解析：∵A＝{1，2，3}，B＝{4，5}，且集合A为定义域，集合B为值域，
∴根据函数的定义可得集合B中的4或5在集合A中就一定有两个元素与之对应．
若4在集合A中有两个元素与之对应，那就会有{1，2}，{2，3}，{1，3}这三种情况．
同理，若5在集合A中有两个元素与之对应，也就会有{1，2}，{2，3}，{1，3}这三种情况．
∴函数可以建立的个数为3＋3＝6(个).
答案：6
9．解析：因为每一个投掷序号n，都有唯一的向上的点数与之对应，
所以根据函数的定义可知，对应f是函数；
这个函数值域不一定是集合{1，2，3，4，5，6}，应该是集合{1，2，3，4，5，6}的非空子集．
10．解析：(1)由x2－1≠0得x≠±1，
所以f(x)＝eq \f(1,x2－1)的定义域为{x|x≠－1且x≠1}．
(2)由eq \b\lc\{(\a\vs4\al\c1(2＋x≥0,1－x≥0))，得－2≤x≤1，
所以f(x)＝eq \r(2＋x)＋eq \r(1－x)的定义域为{x|－2≤x≤1}．
(3)由eq \b\lc\{(\a\vs4\al\c1(x＋1≥0,x＋2≠0))，得x≥－1，所以f(x)的定义域为{x|x≥－1}．
11．解析：根据圆柱的体积公式的实际应用，油面高度为h，会影响油面的宽度w，从而影响油量v，
A：由于v确定，故h确定，w就确定，符合函数的定义，故A正确；
B：由于w确定，h有两个(上下对称)，所以v有两个，
故与函数的定义相矛盾，不是函数，故B错误；
C：由于v确定，故h确定，符合函数的定义，故C正确；
D：由于h确定，故v确定，符合函数的定义，故D正确．
故选B.
答案：B
12．解析：根据对应关系y＝3x＋1，3×1＋1＝4，
3×2＋1＝7，由题意可得3×k＋1＝3k＋1＝10，
∴k＝3.故选B.
答案：B
13．解析：根据函数的定义可得f(a)，f(b)，f(c)均可取－1，0，1中的一个，
则满足f(a)＋f(b)＝f(c)的有：
0＋0＝0，0＋1＝1，1＋0＝1，0－1＝－1，－1＋0＝－1，1－1＝0，－1＋1＝0，共7个．故选D.
答案：D
14．解析：对于A，根据题意可知定义域为A＝{a∈N*|a≥1}，B＝{0，1，2，3，4，5，6，7，8，9}，
因为0∈B，0∉A，所以值域B不是定义域A的子集，所以A错误，
对于BC，由题意可知数位a对应的数字依次为1，4，1，5，9，2，6，…，则函数图象f(a)是一群孤立的点，f(6)＝2，所以BC正确，
对于D，因为b＝1时，a＝1和3，不符合函数的定义，所以D错误．故选BC.
答案：BC
15．解析：f(x)的定义域是R，则－mx2－2x＋1≥0恒成立，
即mx2＋2x－1≤0恒成立，则eq \b\lc\{(\a\vs4\al\c1(m＜0,Δ≤0))，解得m≤－1，
所以实数m的取值范围为m≤－1.
答案：{m|m≤－1}
16．解析：直角三角形的面积为5，设一条直角边长为x，另一条直角边长为y，那么y＝eq \f(10,x).其中，x的取值范围是A＝{x|x＞0}，y的取值范围是B＝{y|y>0}．对应关系f把每一个直角三角形的一条直角边长x，对应到唯一确定的另一条直角边长eq \f(10,x).
基础强化
投掷
序号
1
2
3
4
5
6
7
8
9
10
向上
点数
能力提升