北师大版八年级数学上册课件 第4章末复习

这是一份北师大版八年级数学上册课件 第4章末复习，共29页。

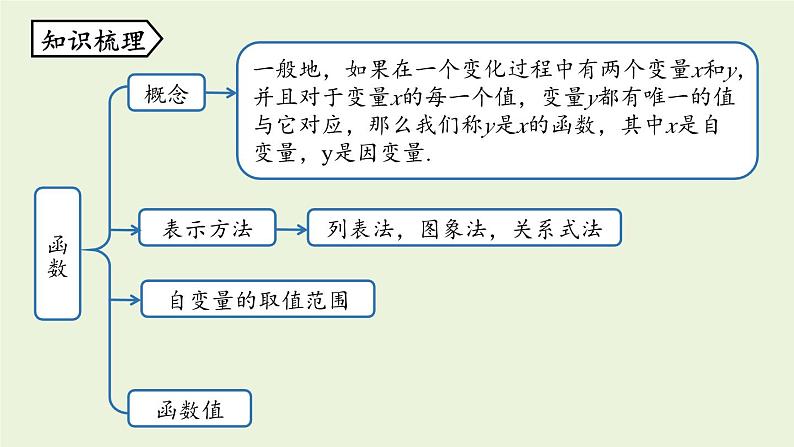
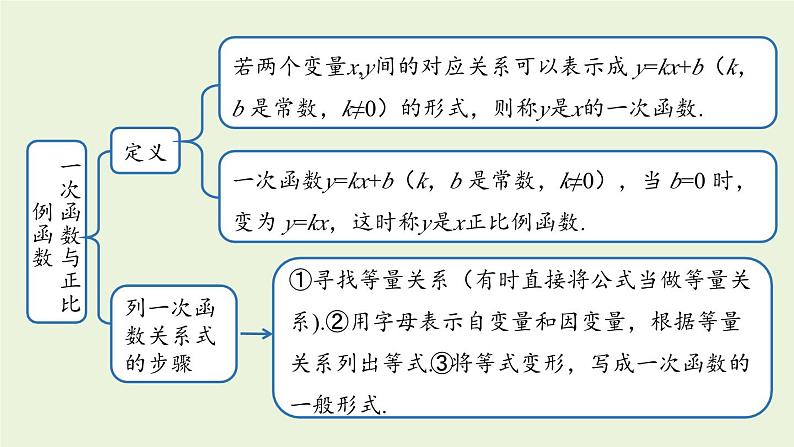
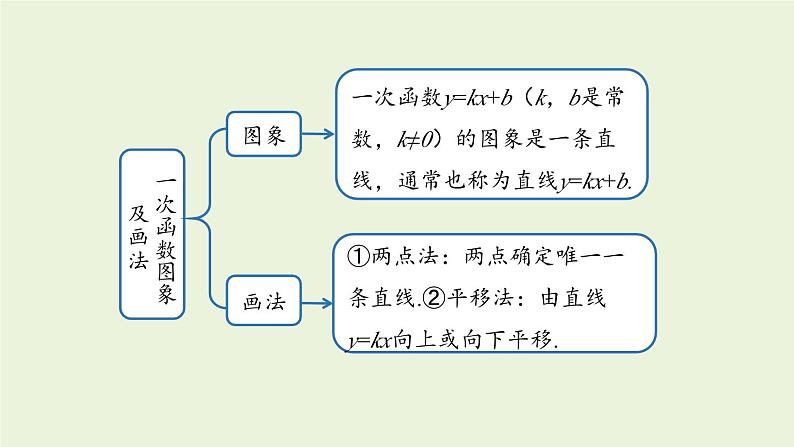
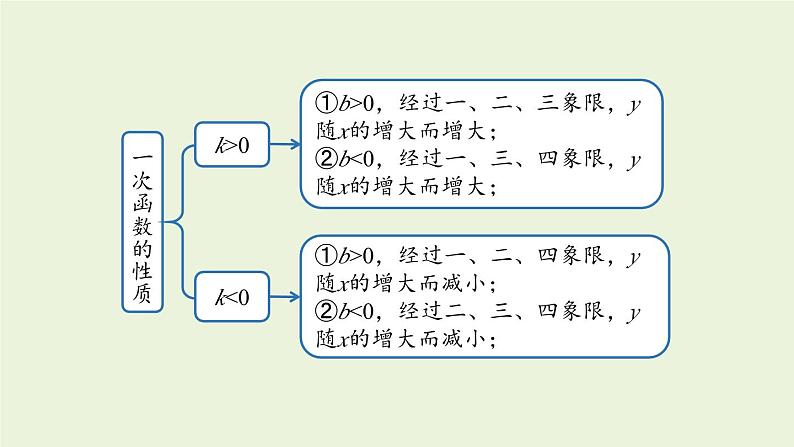
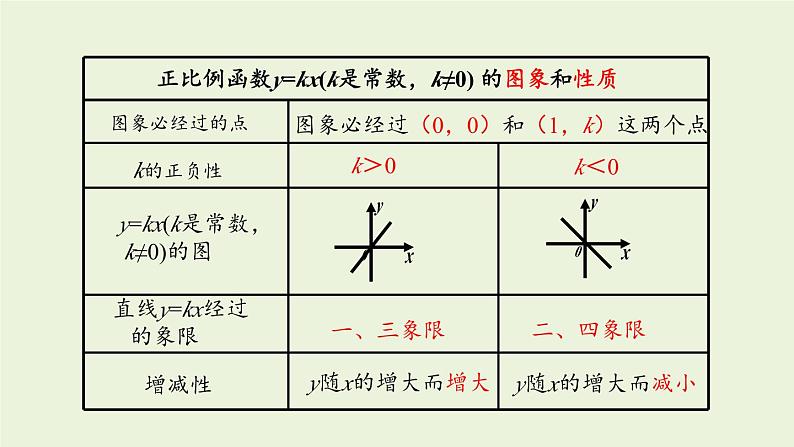
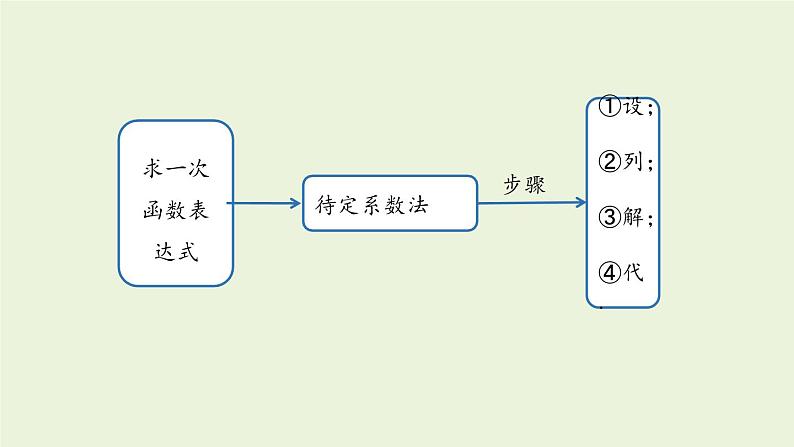
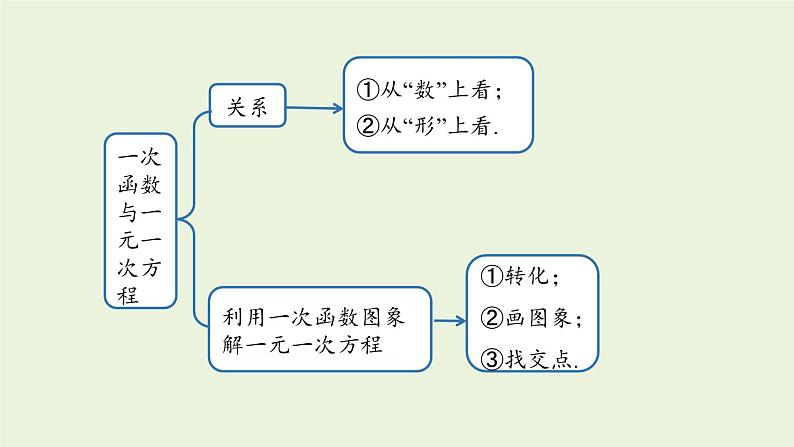
4. 章末复习函数概念一般地，如果在一个变化过程中有两个变量x和y，并且对于变量x的每一个值，变量y都有唯一的值与它对应，那么我们称y是x的函数，其中x是自变量，y是因变量.表示方法列表法，图象法，关系式法自变量的取值范围函数值知识梳理一次函数与正比例函数定义列一次函数关系式的步骤若两个变量x,y间的对应关系可以表示成 y=kx+b（k，b 是常数，k≠0）的形式，则称y是x的一次函数.①寻找等量关系（有时直接将公式当做等量关系).②用字母表示自变量和因变量，根据等量关系列出等式.③将等式变形，写成一次函数的一般形式.一次函数y=kx+b（k，b 是常数，k≠0），当 b=0 时，变为 y=kx，这时称y是x正比例函数.一次函数图象及画法图象画法一次函数y=kx+b（k，b是常数，k≠0）的图象是一条直线，通常也称为直线y=kx+b.①两点法：两点确定唯一一条直线.②平移法：由直线y=kx向上或向下平移.一次函数的性质k>0k<0①b>0，经过一、二、三象限，y随x的增大而增大；②b<0，经过一、三、四象限，y随x的增大而增大；①b>0，经过一、二、四象限，y随x的增大而减小；②b<0，经过二、三、四象限，y随x的增大而减小；一、三象限二、四象限y随x的增大而减小y随x的增大而增大图象必经过（0，0）和（1，k）这两个点k的正负性k＞0k＜0y=kx(k是常数， k≠0)的图求一次函数表达式待定系数法①设；②列；③解；④代.步骤关系利用一次函数图象解一元一次方程①从“数”上看；②从“形”上看.①转化；②画图象；③找交点.一次函数与一元一次方程一次函数图象的应用一个一次函数图象的应用两个一次函数图象的应用①根据图象，判断函数的类型，②利用图象上特殊点的坐标建立关系求出函数表达式，同时由点的意义，即横、纵坐标的意义表示实际意义.随堂练习1.下列变量间的关系不是函数关系的是（ ）.A.圆的半径与圆的面积B.正方形的周长与正方形的边长C.在汽车速度一定的情况下，时间与路程D.等腰三角形的底边长与面积D2.小刚从家去学校，先匀速步行到车站，等了几分钟后坐上了公交车，公交车匀速行驶一段时间后到达学校，小刚从家到学校行驶路程 s（单位：m）与时间 t（单位：min）之间的函数关系的大致图象是（ ）.B3.周日下午，小红和小兰相约在某公交车站一起乘车回学校，小红从家出发先步行到车站，等小兰到车站后两人一起乘公交车回到学校.下图表示小红离开家的路程 y（千米）和所用的时间 x（分钟）之间的函数关系.下列哪个说法是错误的（ ）.A.小红从家到公交车站步行了2千米.B.小红乘坐公交车用了30分钟.C.小红在公交车站等小兰用了10分钟.D.公交车的平均速度是34千米/小时.解：从图上来看，小红出发20分钟后小红从家走到了公交车站，路程变化为2千米；20分~30分之间小红离开家的路程未发生变化，说明此阶段是在公交车站等小兰；30分~ 60分小红和小兰一起乘坐公交车到达学校，用时30分钟，路程为15千米.公交车速度为15÷0.5=30 （千米/时）.故选D.4.下列所有表达式中，是一次函数但不是正比例函数的是（ ）    B5.下列图形中，表示一次函数 y1=mx+n 与正比例函数y2=mnx（m、n为常数，且mn≠0）的图象的是（ ）6.一元一次方程 ax-b=0 的解为 x=5，则函数 y=ax-b 与 x 轴的交点坐标是（ ）.A.（0，5） B.（0 ，-5） CC.（5，0） D.（-5 ，0） 解析：ax-b=0 的解就是当函数 y=ax-b 中 y=0 时 x 的值.7.如图，一次函数y=2x+1的图象与坐标轴分别交于A，B两点，O为坐标原点，则△AOB的面积是（ ）.  A8.已知函数 y=2x+3.（1）试判断点 A（1，5）和点 B（-1，3）是否在此 函数图象上；（2）已知点 C（m，m+3）在此函数图象上，求 m 的值.  2m+3=m+3，解得m=0将 x=m， y=m+3 代入函数解析式中9.小李从西安通过某快递公司给在南昌的外婆邮寄一盒樱桃，快递时，他了解到这个公司除收取每次 6 元的包装费外，樱桃不超过 1kg 收费 22 元，超过 1kg 的部分按照每千克 10 元加收费用.设该公司从西安到南昌快递樱桃的费用为 y（元），所寄樱桃为 x（kg）.（1）求 y 与 x 之间的函数解析式；（2）已知小李给外婆快递了 2.5kg 樱桃，请你求出这次快递的费用是多少元？解:（1）由题意得,当 01 时，y=28+10(x-1)=10x+18； 所以小李此次的快寄费用是 43 元.10.根据记录，从地面向上 11 km 以内，每升高 1km，气温降低6℃；又知道在距离地面 11km 以上的高空，气温几乎不变.若地面气温为 m(℃)，设距地面的高度为 x(km) 处的气温为 y(℃).（1）写出距地面的高度在 11 km 以内的 y 与 x 之间的函数解析式；解：由题意知，y=m-6x（0≤x≤11）.（2）上周日，小敏乘飞机从上海飞回西安途中，某一时刻，她从机舱内屏幕显示的相关数据得知，飞机外气温为-26℃时，飞机距地面的高度为 7 km，求当时这架飞机下方地面的气温；小敏想，假如飞机当时在距地面 12 km 的高空，飞机外的气温是多少度呢？请求出假如当飞机距地面 12 km 时，飞机外的气温.解：将 x=7, y=-26 代入 y=m-6x,得 -26=m-42，解得m=16,即当飞机外气温为-26 ℃时，飞机下方地面温度为16 ℃.因为 12>11，所以此时飞机外的气温为16-6×11=50 (℃).（2）将 x=7 时，y=-26 代入 y=m-6x，得 -26=m-42，解得：m=16.所以当时这架飞机下方地面的气温为 16℃.因为 12>11，所以 y=-50℃，则假如当飞机距地面12km 时，飞机外的气温为 -50℃.11.在“美丽家乡，清洁乡村”活动中，李家村村长提出两种购买垃圾桶的方案，方案一：买分类垃圾桶，需要费用 3000 元，以后每月的垃圾处理费用为 250 元；方案二：买不分类垃圾桶，需要费用 1000 元，以后每月的垃圾处理费用为 500 元.设方案一的购买费和垃圾处理费共 y1 元，方案二的购买费和垃圾处理费共 y2 元，交费时间为 x 个月.（2）在同一平面直角坐标系中，画出函数 y2，y2 的图象；（3）在垃圾桶使用寿命相同的情况下，哪种方案更省钱？解：（1） 由题意可得：y1=250x+3000（x≥0）；y2=500x+1000（x≥0）.（1）直接写出 y1，y2 与 x 的函数解析式；（2）对于 y1=250x+3000（x≥0）,当 x=0 时，y1=3000；当 x=4 时，y1=4000 . 过点（0，3000）,（4，4000）在第一象限内画射线，即是函数 y1=250x+3000（x≥0）的图象.对于 y2=500x+1000（x≥0） ，当 x=0 时，y2=1000；当 x=4 时，y1=3000 . 过点（0，1000），（4，3000）在第一象限内画射线,即是函数 y2=500x+1000（x≥0）的图象.y1=250x+3000（x≥0）,过点（0，3000）,（4，4000）； y2=500x+1000（x≥0）,过点（0，1000）,（4，3000）.所以函数 y1=250x+3000（x≥0）,y2=500x+1000（x≥0）的图象的交点坐标为（8，5000）.观察图象可得：当x>8时，y1y2，方案二更省钱.