初中数学北师大版八年级上册4 平行线的性质集体备课课件ppt

这是一份初中数学北师大版八年级上册4 平行线的性质集体备课课件ppt，共20页。PPT课件主要包含了知识回顾，学习目标，两直线平行，课堂导入，新知探究，定理1，定理23，随堂练习，∠5∠260°，∠4与∠5互补等内容，欢迎下载使用。
根据右图，填空：① 如果∠1＝∠C，　那么 ∥ .（ 　　　　　 　 ）② 如果∠1＝∠B ， 那么 ∥ .（ 　　 　　 　 ）③ 如果∠2＋∠B＝180°，　那么 ∥ .（ 　　 ）
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
1.掌握平行线的性质定理，会运用两条直线是平行关系判断角相等或互补.
2.了解性质定理与判定定理的联系，初步感受互逆的思维过程.
3.进一步理解证明的步骤、格式和方法，发展演绎推理能力.
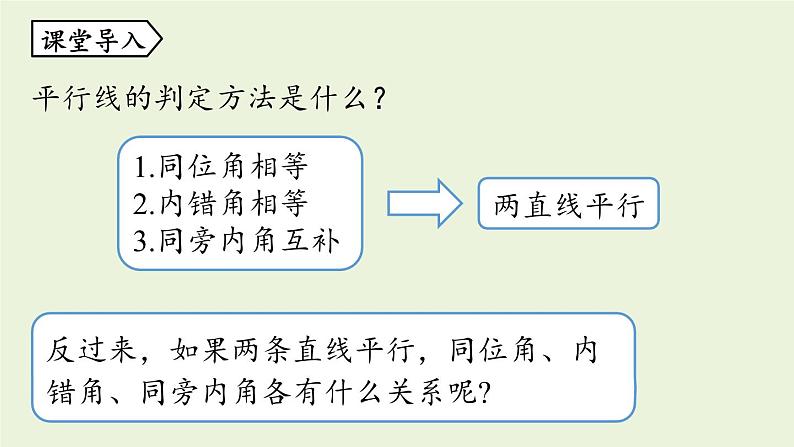
1.同位角相等2.内错角相等3.同旁内角互补
平行线的判定方法是什么？
反过来，如果两条直线平行，同位角、内错角、同旁内角各有什么关系呢?
证明：两条平行直线被第三条直线所截，同位角相等.
（1）你能作出相关的图形吗？（2）你能根据所作的图形写出已知、求证吗？（3）你能说说证明的思路吗？
已知：如图，直线 AB∥CD，∠1和∠2是直线 AB，CD 被直线 EF 截出的同位角.求证：∠1=∠2.
如果∠1≠∠2，AB与CD的位置关系会怎样呢？
证明：假设∠1≠∠2，那么我们可以过M点作直线GH，使∠EMH =∠2，如图所示.
根据“同位角相等，两直线平行”可知GH∥CD.
又因为AB∥CD，所以这样经过点M存在两条直线AB和GH都与直线CD平行.
这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
这说明∠1≠∠2的假设不成立，所以∠1=∠2.
两条平行直线被第三条直线所截，同位角相等.
简述为：两直线平行，同位角相等.
证明：两条平行直线被第三条直线所截，内错角相等.
已知：如图，直线 l1∥l2，∠1和∠2是直线 l1 ， l2 被直线 l 截出的内错角.求证：∠1=∠2.
∵ l1∥l2（已知），
∴ ∠1=∠3（两直线平行，同位角相等）.
∴ ∠1=∠2（等量代换）.
又∵ ∠2=∠3（对顶角相等），
两条平行直线被第三条直线所截，内错角相等.简述为：两直线平行，内错角相等.
定理3：两条平行直线被第三条直线所截，同旁内角互补.简述为：两直线平行，同旁内角互补.
类似地，还可以证明：
例1 如图是一块梯形铁片的残余部分，量得∠A=100°，∠B=115°，梯形的另外两个角分别是多少度？
解：因为梯形上、下底互相平行，所以∠A 与∠D 互补,∠B 与∠C 互补.
即梯形的另外两个角分别是 80°，65°.
所以∠D=180 °-∠A=180°-100°=80°，∠C= 180 °-∠B=180°-115°=65°.
平行线的判定和性质的区别和联系联系：平行线的判定和性质反映了角的数量关系和直线的位置关系之间的相互转换.区别：平行线的判定以两直线平行为结论，即由两角相等或互补得到两直线平行，是由数量关系得到位置关系；平行线的性质以两直线平行为条件，即由两直线平行得到两角相等或互补， 是由位置关系得到数量关系.
1.如图，CD//AB，点 O 在 AB 上，OE 平分∠BOD，OF⊥OE，∠D=110°，则∠AOF 的度数是( )A.20° B.25° C.30° D.35°
2.如图，如果∠1=∠3，∠2= 60°，那么，∠4的度数为( )A.60°B.100°C.120°D.130°
3.如图，AB//CD，∠ABD 的平分线与∠BDC 的平分线交于点 E，则∠1+∠2= .
∠ABD+∠CDB=180°
解：(1)根据两直线平行，内错角相等，可得∠ABG=48°，∴ 从 B 地测得公路的走向是南偏西 48°.
4.如图，在 A，B 两地之间要修一条笔直的公路，从 A 地测得公路走向是北偏东 48°，A，B 两地同时开工，若干天后公路准确接通.(1)从 B 地测得公路的走向是南偏西多少度?
(2)若公路 AB 长 8 km，另一条公路 BC 长 6 km，且从 B 地测得公路 BC 的走向是北偏西 42°，试求 A 地到公路 BC 的距离.
解：(2)∵ ∠ABC=180°-∠ABG -∠EBC =180°-48°-42°=90°，∴ AB⊥BC，∴ AB 的长度就是点 A 到直线 BC 的距离.∵ AB =8 km， ∴ A 地到公路 BC 的距离是 8 km.
5. 已知：如图，∠1=∠2，∠3=∠4. 求证：EG∥FH.证明：∵∠1=∠2(已知)，∠AEF=∠1 (对顶角相等)，∴∠AEF=∠2 (等量代换).∴AB∥CD (同位角相等，两直线平行).∴∠BEF=∠CFE (两直线平行，内错角相等). ∵∠3=∠4(已知)，∴∠BEF－∠4=∠CFE－∠3.即∠GEF=∠HFE (等式的性质).∴EG∥FH (内错角相等，两直线平行).