江苏省南京市玄武区南京外国语学校2023-2024学年九年级上学期期中数学试题(无答案)

这是一份江苏省南京市玄武区南京外国语学校2023-2024学年九年级上学期期中数学试题(无答案)，共4页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
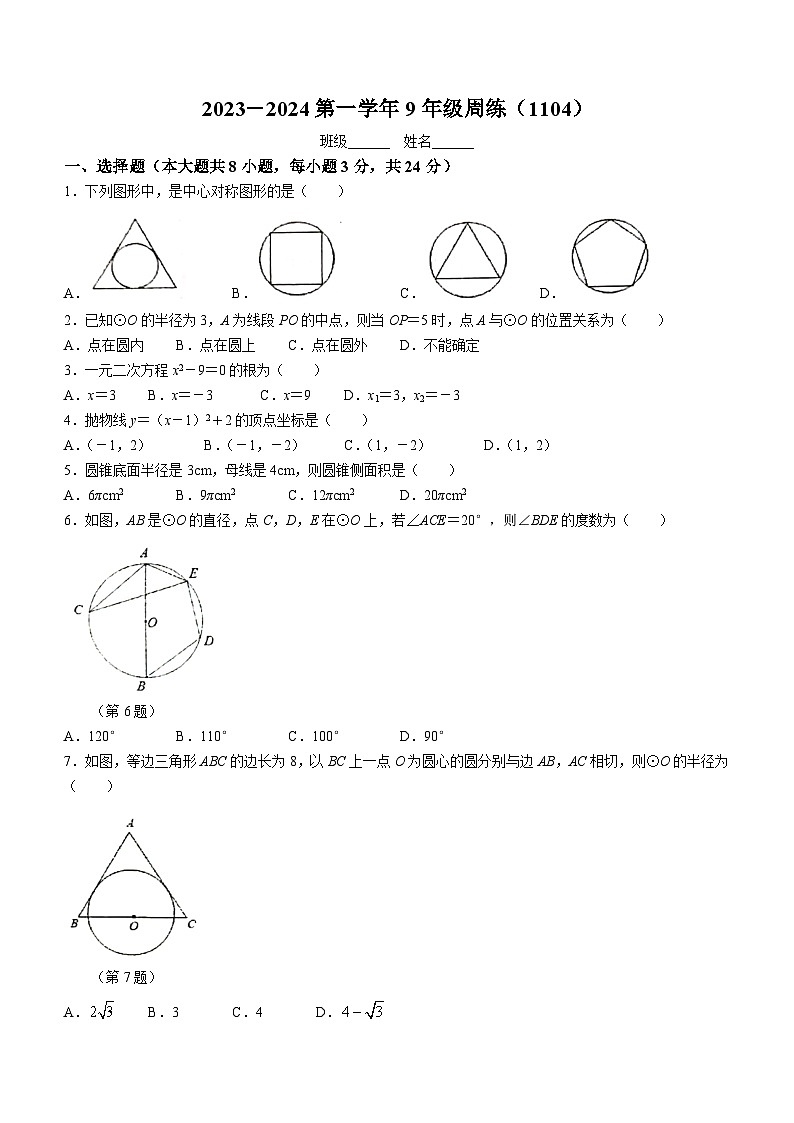
一、选择题（本大题共8小题，每小题3分，共24分）
1．下列图形中，是中心对称图形的是（ ）
A．B．C．D．
2．已知⊙O的半径为3，A为线段PO的中点，则当OP＝5时，点A与⊙O的位置关系为（ ）
A．点在圆内B．点在圆上C．点在圆外D．不能确定
3．一元二次方程x2－9＝0的根为（ ）
A．x＝3B．x＝－3C．x＝9D．x1＝3，x2＝－3
4．抛物线y＝（x－1）2＋2的顶点坐标是（ ）
A．（－1，2）B．（－1，－2）C．（1，－2）D．（1，2）
5．圆锥底面半径是3cm，母线是4cm，则圆锥侧面积是（ ）
A．6πcm2B．9πcm2C．12πcm2D．20πcm2
6．如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠ACE＝20°，则∠BDE的度数为（ ）
（第6题）
A．120°B．110°C．100°D．90°
7．如图，等边三角形ABC的边长为8，以BC上一点O为圆心的圆分别与边AB，AC相切，则⊙O的半径为（ ）
（第7题）
A．B．3C．4D．
8．如图是二次函数y＝ax2＋bx＋c图像的一部分，其对称轴为直线x＝－1，且过点（－3，0），下列说法：①abc＜0；②2a－b＝0；③4a＋2b＋c＜0；④若（－5，y1），（2.5，y2）是抛物线上两点，则y1＞y2，其中说法正确的是（ ）
（第8题）
A．①②③B．②③C．①②④D．①②③④
二、填空题（本大题共8小题，每小题3分，共24分）
9．方程x2＝x的解是______．
10．四边形ABCD内接于圆，若∠A＝110°，则∠C＝______°．
11．已知扇形的圆心角为120°，半径为6cm，则该扇形的弧长为______cm（结果保留π）．
12．一元二次方程2x2＋4x－1＝0的两根为x1，x2，则x1＋x2的值是______．
13．抛物线y＝x2沿x轴向右平移1个单位长度，则平移后抛物线对应的表达式是______．
14．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB＝8，AE＝1，则弦CD的长是______．
（第14题）
15．如图，半径为4的⊙O与含有30°角的直角三角板ABC的边AC切于点A，将直角三角板沿CA边所在的直线向左平移，当平移到AB与⊙O相切时，该直角三角板平移的距离为______．
（第15题）
16．如图，在平面直角坐标系xOy中，已知点A（1，0），B（3，0），C为平面内的动点，且满足∠ACB＝90°，D为直线y＝x上的动点，则线段CD长的最小值为______．
（第16题）
三、解答题（本大题共5小题，共52分）
17．（本题10分）解方程：（1）2x2＋1＝3x（2）3（y－1）2＝1－y
18．（本题10分）如图，在Rt△ABC中，∠C＝90°，
（1）求作⊙P，使圆心P在BC上，且⊙P与AC、AB都相切；（要求：尺规作图，不写作法，保留作图痕迹）
（2）在（1）的条件下，若AC＝4，BC＝3．求⊙P的半径．
19．（10分）如图，CD是⊙O的直径，且CD＝2cm，点P为CD的延长线上一点，过点P作⊙O的切线PA，PB，切点分别为点A，B．
（第19题）
（1）连接AC，若∠APO＝30°，求证：△ACP是等腰三角形；
（2）填空：①当DP＝______cm时，四边形AOBD是菱形；
②当DP＝______cm时，四边形AOBP是正方形．
20．（10分）某市场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元。为了扩大销售，增加赢利，尽快减少库存，商场决定采取适当降价措施。经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件。求：
（1）若商场平均每天要赢利1200元，每件衬衫应降价多少元？
（2）当每件衬衫降价多少元时，商场平均每天赢利最多，最多是多少？
21．（12分）如图，抛物线与x轴交于点A（－1，0），B（3，0）两点，与y轴交于点C（0，－3）．
（1）求该抛物线的函数表达式及顶点M的坐标；
（2）求△BCM面积与△ABC面积的比；
（3）若P是x轴上一个动点，过P作射线交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A、P、Q、C为顶点的四边形为平行四边形？若存在请直接写出Q点的坐标；若不存在，请说明理由．