



还剩12页未读,
继续阅读
所属成套资源:北师大版八年级数学上册课件
成套系列资料,整套一键下载
北师大版八年级数学上册课件 7.5.2 三角形内角和定理
展开
这是一份北师大版八年级数学上册课件 7.5.2 三角形内角和定理,共20页。
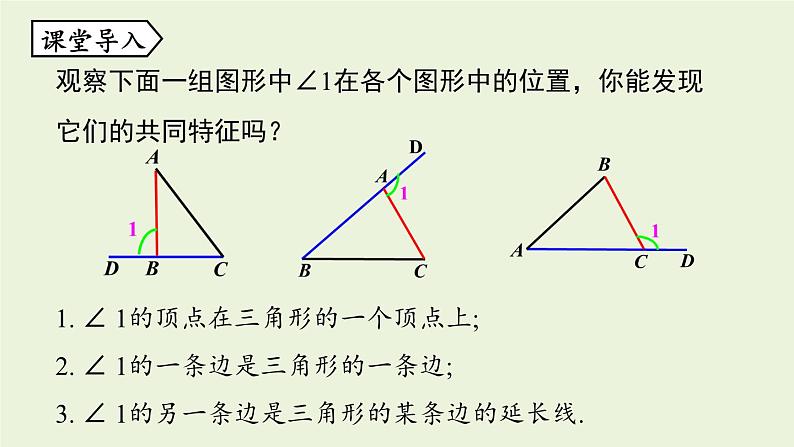
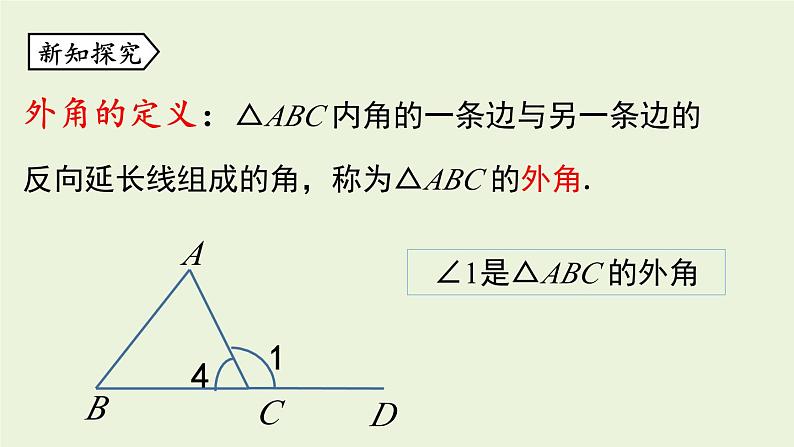
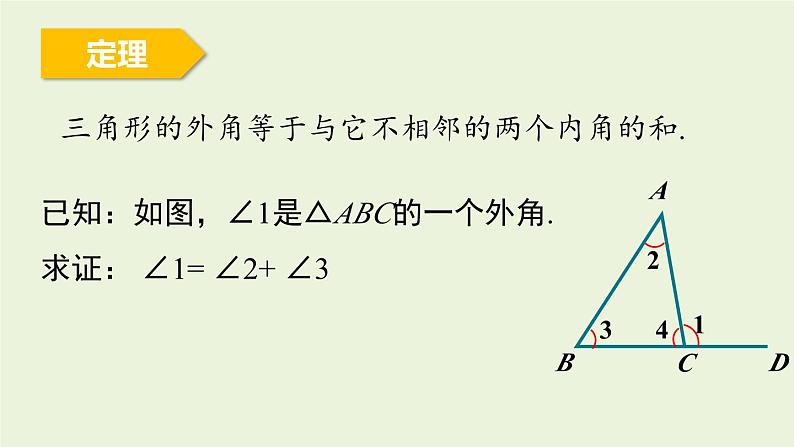
7.5.2 三角形内角和定理知识回顾内容证明三角形内角和定理的证明三角形的内角和等于180°借助平行线将三个内角拼成一个平角1.了解并掌握三角形的外角的定义.2.掌握三角形的外角的性质,利用外角的性质进行简单的证明和计算.学习目标课堂导入观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?1. ∠ 1的顶点在三角形的一个顶点上;2. ∠ 1的一条边是三角形的一条边;3. ∠ 1的另一条边是三角形的某条边的延长线.外角的定义:△ABC 内角的一条边与另一条边的反向延长线组成的角,称为△ABC 的外角.∠1是△ABC 的外角新知探究探究1: 画出△ABC所有的外角,并指出有哪几个? 有6个,它们是∠1,∠2, ∠3, ∠4, ∠5, ∠6.探究2: △ABC的6个外角有什么关系?∠1和∠4是对顶角,相等;∠2和 ∠5是对顶角,相等;∠3和∠6是对顶角,相等.总结三角形的外角应具备的条件:①角的顶点是三角形的顶点;②角的一边是三角形的一边;③另一边是三角形中一边的延长线. ∠ACD是△ABC的一个外角, 每一个三角形都有6个外角.定理三角形的外角等于与它不相邻的两个内角的和.已知:如图,∠1是△ABC的一个外角.求证: ∠1= ∠2+ ∠3证明:∵ ∠4 +∠2+ ∠3=180°(三角形内角和定理), ∴ ∠2+ ∠3= 180°-∠4(等式的性质). ∵ ∠1+ ∠4= 180°(1平角= 180°), ∴ ∠1 = 180°-∠4(等式的性质), ∴ ∠ 1= ∠2+ ∠3 (等量代换).定理三角形的一个外角大于任何一个和它不相邻的内角.已知:如图,∠1是△ABC的一个外角.求证: ∠1> ∠2, ∠1> ∠3证明: ∵ ∠1 =∠2+ ∠3(三角形的一个外角等于和它不相邻的两内角和). ∴ ∠1>∠2, ∠1>∠3 (和大于部分).例1 一个零件的形状如图所示,按规定∠A 应等于90°,∠B,∠C 应分别是21°和32°,检验工人量得∠BDC=148°,就断定这个零件不合格,这是为什么呢? 例2 已知:如图,P是△ABC 内一点,连接PB, PC.求证:∠BPC > ∠A.证明:如图,延长BP,交AC于点D.∵∠BPC是△PDC的一个外角(外角的定义),∴ ∠BPC>∠ PDC(三角形的一个外角大于任何一个和它不相邻的内角).∵∠PDC是△ABD的一个外角(外角的定义),∴∠PDC>∠ A(三角形的一个外角大于任何一个和它不相邻的内角),∴∠BPC>∠A.D 例3 如图, ∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE= ∠2+ ∠3,∠CBF= ∠1+ ∠3,∠ACD= ∠1+ ∠2.又知∠1+ ∠2+ ∠3=180 °,所以∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.你还有其他解法吗?方法二 如图,∠BAE+∠1=180 °, ①∠CBF +∠2=180 ° ,②∠ACD +∠3=180 ° .③又知∠1+ ∠2+ ∠3=180 °,①+ ②+ ③得∠BAE+ ∠CBF+ ∠ACD+(∠1+ ∠2+ ∠3)=540 °,所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.方法三 如图所示,过点A 作射线AP,使AP∥BD. ∵ AP∥BD, ∴ ∠CBF =∠PAB,∠ACD =∠EAP. ∴ ∠BAE+∠CBF+∠ACD=∠BAE+∠PAB+∠EAP=360°. P(随堂练习1.如图,在△ABC 中,∠B=40°,∠ACD=120°,则∠A的度数是 .80°2.在△ABC中,∠A=50°,∠ABC=70°, BD平分∠ABC,则∠BDC的度数是 .85°50°?70°(((3. 已知:如图,∠1,∠2,∠3是△ABC的三个外角。求∠1+∠2+∠3的度数.解:∵∠1,∠2,∠3是△ABC的三个外角, ∴ ∠1= ∠ABC+ ∠ACB,∠2= ∠BAC+ ∠ACB,∠3= ∠ABC+ ∠CAB,∵三角形内角和为180°,∴ ∠BAC+ ∠ABC+ ∠ACB=180°,∴ ∠1+∠2+∠3=2(∠BAC+ ∠ABC+ ∠ACB)=360°.解:因为∠ADC是△ABD的外角,4 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°.求:(1)∠B 的度数;(2)∠C的度数.在△ABC中,∠B+∠BAC+∠C=180°,所以∠C=180º-40º-70º=70°.所以∠ADC=∠B+∠BAD=80°.又因为∠B=∠BAD, ABCD三角形的外角定义角一边必须是三角形的一边,另一边必须是三角形另一边的延长线性质1.三角形的外角等于与它不相邻的两个内角的和三角形的外角和三角形的外角和等于360 °2.三角形的外角大于与它不相邻的任何一个内角
7.5.2 三角形内角和定理知识回顾内容证明三角形内角和定理的证明三角形的内角和等于180°借助平行线将三个内角拼成一个平角1.了解并掌握三角形的外角的定义.2.掌握三角形的外角的性质,利用外角的性质进行简单的证明和计算.学习目标课堂导入观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?1. ∠ 1的顶点在三角形的一个顶点上;2. ∠ 1的一条边是三角形的一条边;3. ∠ 1的另一条边是三角形的某条边的延长线.外角的定义:△ABC 内角的一条边与另一条边的反向延长线组成的角,称为△ABC 的外角.∠1是△ABC 的外角新知探究探究1: 画出△ABC所有的外角,并指出有哪几个? 有6个,它们是∠1,∠2, ∠3, ∠4, ∠5, ∠6.探究2: △ABC的6个外角有什么关系?∠1和∠4是对顶角,相等;∠2和 ∠5是对顶角,相等;∠3和∠6是对顶角,相等.总结三角形的外角应具备的条件:①角的顶点是三角形的顶点;②角的一边是三角形的一边;③另一边是三角形中一边的延长线. ∠ACD是△ABC的一个外角, 每一个三角形都有6个外角.定理三角形的外角等于与它不相邻的两个内角的和.已知:如图,∠1是△ABC的一个外角.求证: ∠1= ∠2+ ∠3证明:∵ ∠4 +∠2+ ∠3=180°(三角形内角和定理), ∴ ∠2+ ∠3= 180°-∠4(等式的性质). ∵ ∠1+ ∠4= 180°(1平角= 180°), ∴ ∠1 = 180°-∠4(等式的性质), ∴ ∠ 1= ∠2+ ∠3 (等量代换).定理三角形的一个外角大于任何一个和它不相邻的内角.已知:如图,∠1是△ABC的一个外角.求证: ∠1> ∠2, ∠1> ∠3证明: ∵ ∠1 =∠2+ ∠3(三角形的一个外角等于和它不相邻的两内角和). ∴ ∠1>∠2, ∠1>∠3 (和大于部分).例1 一个零件的形状如图所示,按规定∠A 应等于90°,∠B,∠C 应分别是21°和32°,检验工人量得∠BDC=148°,就断定这个零件不合格,这是为什么呢? 例2 已知:如图,P是△ABC 内一点,连接PB, PC.求证:∠BPC > ∠A.证明:如图,延长BP,交AC于点D.∵∠BPC是△PDC的一个外角(外角的定义),∴ ∠BPC>∠ PDC(三角形的一个外角大于任何一个和它不相邻的内角).∵∠PDC是△ABD的一个外角(外角的定义),∴∠PDC>∠ A(三角形的一个外角大于任何一个和它不相邻的内角),∴∠BPC>∠A.D 例3 如图, ∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE= ∠2+ ∠3,∠CBF= ∠1+ ∠3,∠ACD= ∠1+ ∠2.又知∠1+ ∠2+ ∠3=180 °,所以∠BAE+ ∠CBF+ ∠ACD=2(∠1+ ∠2+ ∠3)=360 °.你还有其他解法吗?方法二 如图,∠BAE+∠1=180 °, ①∠CBF +∠2=180 ° ,②∠ACD +∠3=180 ° .③又知∠1+ ∠2+ ∠3=180 °,①+ ②+ ③得∠BAE+ ∠CBF+ ∠ACD+(∠1+ ∠2+ ∠3)=540 °,所以∠BAE+ ∠CBF+ ∠ACD=540 °-180°=360°.方法三 如图所示,过点A 作射线AP,使AP∥BD. ∵ AP∥BD, ∴ ∠CBF =∠PAB,∠ACD =∠EAP. ∴ ∠BAE+∠CBF+∠ACD=∠BAE+∠PAB+∠EAP=360°. P(随堂练习1.如图,在△ABC 中,∠B=40°,∠ACD=120°,则∠A的度数是 .80°2.在△ABC中,∠A=50°,∠ABC=70°, BD平分∠ABC,则∠BDC的度数是 .85°50°?70°(((3. 已知:如图,∠1,∠2,∠3是△ABC的三个外角。求∠1+∠2+∠3的度数.解:∵∠1,∠2,∠3是△ABC的三个外角, ∴ ∠1= ∠ABC+ ∠ACB,∠2= ∠BAC+ ∠ACB,∠3= ∠ABC+ ∠CAB,∵三角形内角和为180°,∴ ∠BAC+ ∠ABC+ ∠ACB=180°,∴ ∠1+∠2+∠3=2(∠BAC+ ∠ABC+ ∠ACB)=360°.解:因为∠ADC是△ABD的外角,4 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°.求:(1)∠B 的度数;(2)∠C的度数.在△ABC中,∠B+∠BAC+∠C=180°,所以∠C=180º-40º-70º=70°.所以∠ADC=∠B+∠BAD=80°.又因为∠B=∠BAD, ABCD三角形的外角定义角一边必须是三角形的一边,另一边必须是三角形另一边的延长线性质1.三角形的外角等于与它不相邻的两个内角的和三角形的外角和三角形的外角和等于360 °2.三角形的外角大于与它不相邻的任何一个内角
相关资料
更多









