24.3.2 余弦、正切函数 华师大版数学九年级上册课件

这是一份24.3.2 余弦、正切函数 华师大版数学九年级上册课件，共28页。

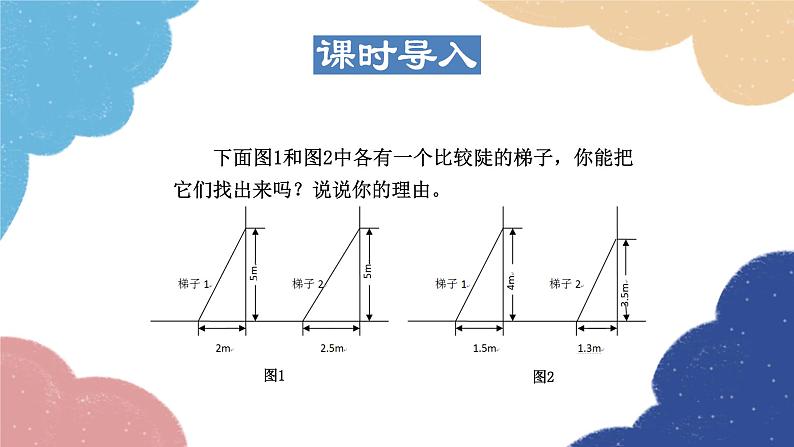
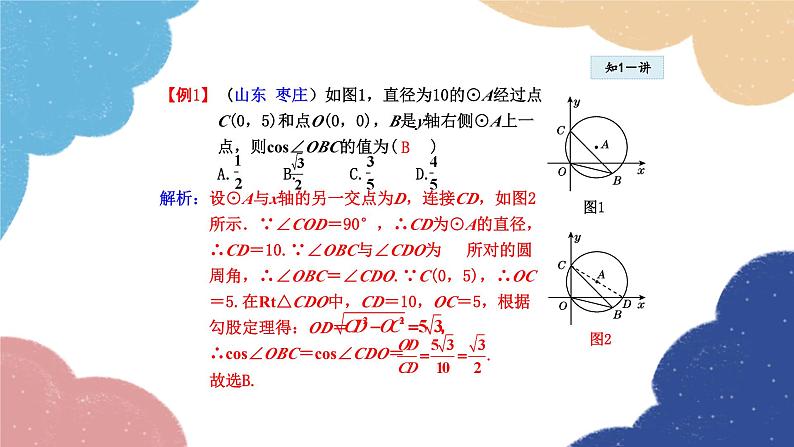
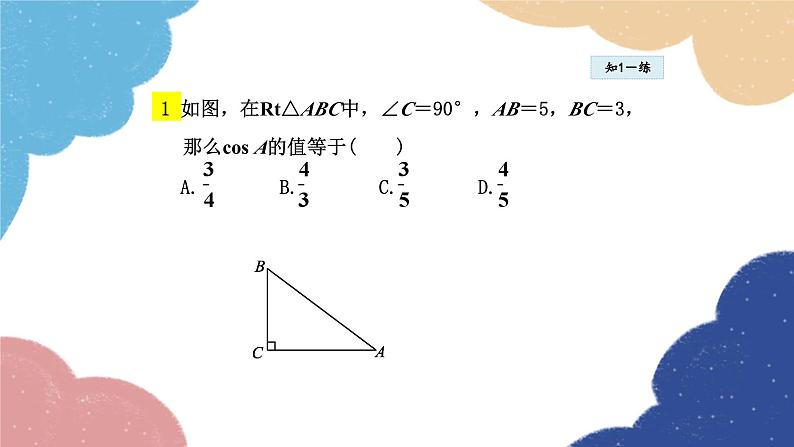
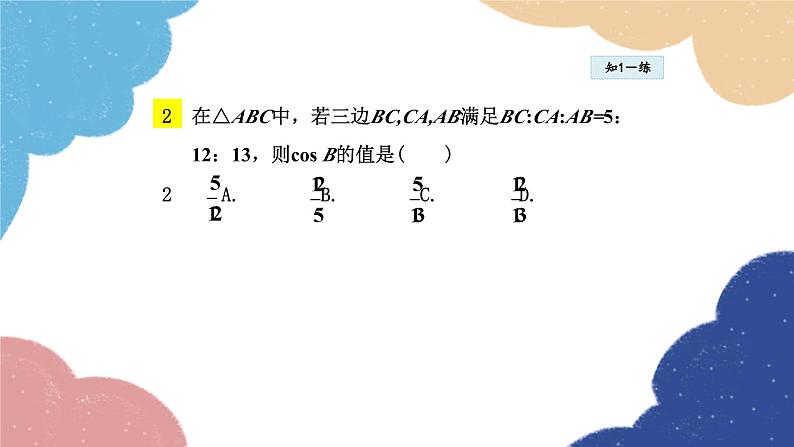
第二十四章 解直角三角形24.3 锐角三角函数第2课时 余弦、正切函数1课堂讲解余弦函数 正切函数 锐角三角函数间的关系2课时流程逐点导讲练课堂小结作业提升 下面图1和图2中各有一个比较陡的梯子，你能把它们找出来吗？说说你的理由。图1图21知识点余弦 余弦：∠A的邻边与斜边的比叫做∠A的余弦，记作cos A，即cos A＝ .知1－讲【例1】（山东 枣庄）如图1，直径为10的⊙A经过点 C(0，5)和点O(0，0)，B是y轴右侧⊙A上一 点，则cos∠OBC的值为(　　) A.　　　B.　　　C.　　　D.解析：设⊙A与x轴的另一交点为D，连接CD，如图2 所示．∵∠COD＝90°，∴CD为⊙A的直径， ∴CD＝10.∵∠OBC与∠CDO为 所对的圆 周角，∴∠OBC＝∠CDO.∵C(0，5)，∴OC ＝5.在Rt△CDO中，CD＝10，OC＝5，根据 勾股定理得：OD＝ ∴cos∠OBC＝cos∠CDO＝ 故选B.知1－讲B图1图2知1－讲 本题运用构造法得到直角三角形，然后运用圆周角定理的推论，勾股定理以及三角函数的定义解答． 知1－练1 如图，在Rt△ABC中，∠C＝90°，AB＝5，BC＝3，那么cos A的值等于(　　)　　　　　　　　　　　　　　　　　　 A. B. C. D.知1－练在△ABC中，若三边BC,CA,AB满足BC:CA:AB=5： 12：13，则cos B的值是(　　) A. B. C. D.知1－练3．如图，已知△ABC的三个顶点均在格点 上，则cos A的值为(　　) A. B. C. D.2知识点正切函数知2－导如图，小明想通过测量B1C1及AC1，算出它们的比，来说明梯子的倾斜程度；而小亮则认为，通过测量B2C2及AC2，算出它们的比，也能说明梯子的倾斜程度。你同意小亮的看法吗？（1）直角三角形AB1C1和直角三角形AB2C2有什么关系？（2） 和 有什么关系？（3）如果改变B2在梯子上的位置呢？ 由此你能得出什么结论？知2－讲 正切：∠A的对边与邻边的比叫做∠A的正切， 记做tan A，即tan A＝ ．知2－讲【例2】如图24.3.3，在Rt△ABC中，∠C＝90°， AC ＝15，BC＝8.试求出∠A的三个三角函数值. 解：【例3】在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对 边分别为a，b，c，请根据下列条件分别求出∠A 的三个三角函数值：(1)a＝6，b＝8；(2)b＝2， c＝ .知2－讲导引：锐角三角函数揭示了直角三角形的三边关系， 所以先利用勾股定理求出未知边的长度，然 后根据定义求∠A的三角函数值．解：(1)如图，在Rt△ABC中， ∵∠C＝90°，a＝6，b＝8， ∴ ∴ 知2－讲 (2)如图，在Rt△ABC中， ∵∠C＝90°，b＝2，c= ∴ ∴ 知2－讲知2－讲 已知直角三角形的任意两边长求某个锐角的三角函数值时，运用数形结合思想，首先画出符合题意的直角三角形，然后根据勾股定理求出未知边长，最后结合锐角三角函数的定义求三角函数值．知2－练1．在Rt△ABC中，∠C＝90°，若斜边AB 是直角边BC的3倍，则tan B的值是(　　) A. B. 3 C. D.知2－练2. (中考·鄂州)如图，在Rt△ABC中，∠BAC＝90°， AD⊥BC于点D，若BD∶CD＝3∶2，则tan B＝ (　　) A. B. C. D.知2－练3．如图，BD是菱形ABCD的对角线，CE⊥AB于点E，交BD于点F，且点E是AB的中点， 则tan ∠BFE的值是(　　) A. B. 2 C. D.3知识点锐角三角函数间的关系知3－讲1.同角的正弦、余弦、正切的关系：同角的正弦与余弦值的比等于该角的正切值，即tan A= 在Rt△ABC中，∠C=90°，a,b,c分别是∠A，∠B，∠C的对边，则sin A= cos A= ∴tan A=知3－讲(1)“sin A”“cos A”“tan A”是整体符号，不能理解为 “sin·A”“cos ·A”“tan ·A”．(2)当锐角是用一个大写英文字母或一个小写希腊字母 表示时，它的三角函数习惯上省略角的符号，如sin A，cos α，tan B等；当锐角是用三个大写英文字母 或数字表示时，它的三角函数不能省略角的符号， 如sin ∠ABC，sin ∠1等．(3)三角函数符号后面可以写成度数，如sin 20°等．知3－讲易错警示：(1)在sin A，cos A，tan A中，三角函数的符号一定要 小写，不能大写．(2)正弦、余弦、正切函数是直角三角形中相对于锐角 而定义的，反映了直角三角形边角之间的关系，是 两条线段的比值，没有单位．【例4】 如图，在△ABC中，AC＝5，∠B＝45°，sin C ＝ ，则△ABC的面积是(　　) A. B．12 C．14 D．21知3－讲A导引：如图，过点A作AD⊥BC于点D. ∵∠B＝45°，∴∠BAD＝45°，∴AD＝BD. ∵sin C ，∴ 解得AD＝BD＝3， ∴DC ∴BC＝BD＋DC＝7. ∴S△ABC＝ BC·AD＝ ×7×3＝ .知3－讲知3－讲 锐角三角函数表示的是边与角之间的关系，三者之间可以相互转化．在Rt△ABC中，∠C＝90°，∠A，∠B，∠C的对边分别为a，b，c，所以sin A＝ ，则a＝c·sin A，c＝ ；cos A＝ ，则b＝c·cos A，c＝ ；tan A＝ ，则a＝b·tan A，b＝ .这九个式子应该灵活运用．知3－练1.在Rt△ABC中，∠C＝90°，sin A＝ ，则cos B的值是（ ） A. B. C. D.知3－练2．在Rt△ABC中，∠C＝90°，下列式子不一定成立 的是(　　) A．tan A＝ B．sin2 A＋cos2 A＝1 C．sin2 A＋sin2 B＝1 D．tan A·tan B＝1求锐角的三角函数值的三种方法：1．在直角三角形里，确定各个边，根据定义直接求 出．2．利用相似、全等等关系，寻找与所求角相等的角 (若该角的三角函数值知道或者易求)．3．利用互余的两个角间的特殊关系求．