



初中数学青岛版九年级上册第1章 图形的相似1.2 怎样判定三角形相似备课ppt课件
展开1、理解并掌握平行线分线段成比例的基本事实及其推论,并会灵活应用。 2、通过应用,培养识图能力和推理论证能力。 3、培养学生积极的思考、动手、观察的能力,使学生感悟几何知识在生活中的价值。
1、什么是成比例线段?2、你能不通过测量快速将一根绳子分成两部分,使得 这两部分的比是2∶3吗?
(1) 如图1-4,直线 l1,l2 被平行直线 l3,l4 所截,交点分别为 A,B,C,D . 过线段AB 的中点 E,作直线l5//l4,交l2于点F. F是线段DC的中点吗?如果是,证明你的结论.
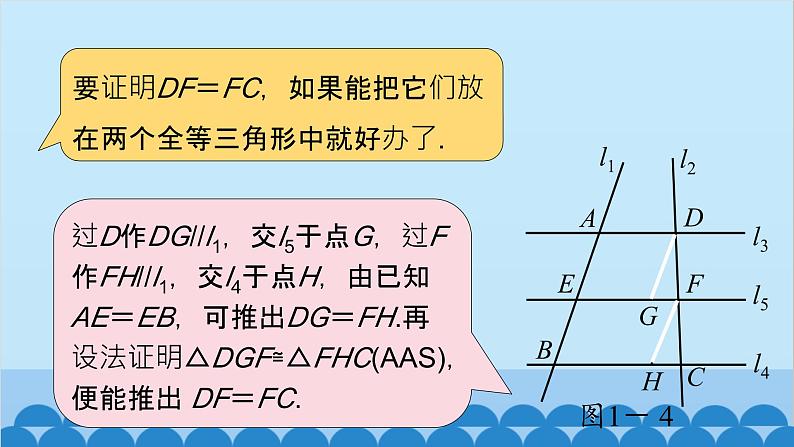
要证明DF=FC,如果能把它们放在两个全等三角形中就好办了.
过D作DG//l1,交l5于点G,过F作FH//l1,交l4于点H,由已知AE=EB,可推出DG=FH.再设法证明△DGF≌△FHC(AAS),便能推出 DF=FC.
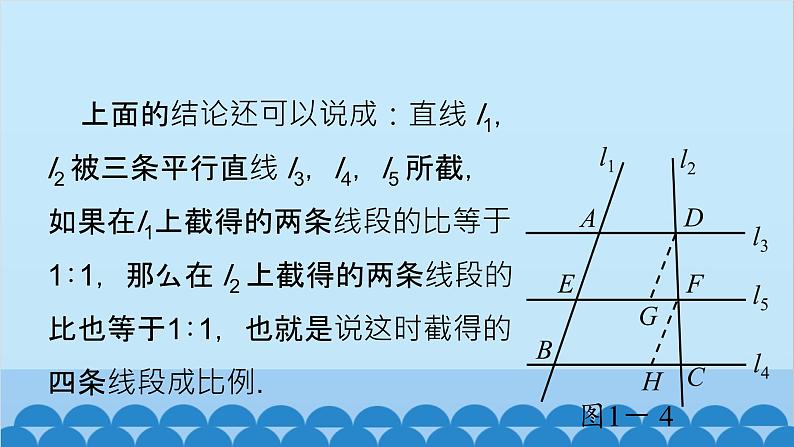
上面的结论还可以说成:直线 l1,l2 被三条平行直线 l3,l4,l5 所截,如果在l1上截得的两条线段的比等于 1∶1,那么在 l2 上截得的两条线段的比也等于1∶1,也就是说这时截得的四条线段成比例.
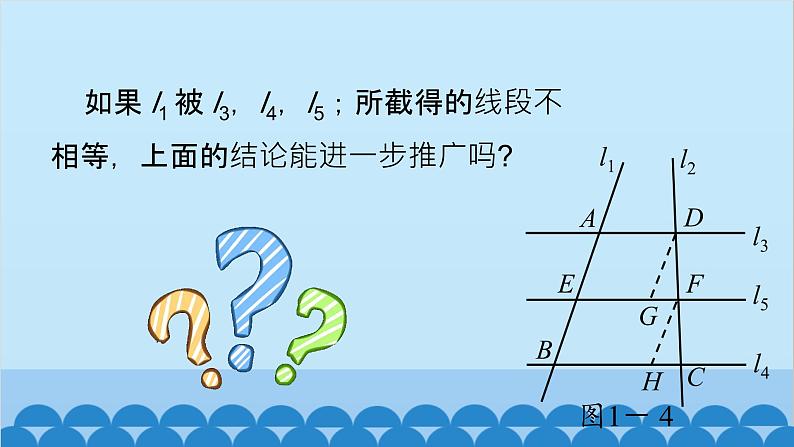
如果 l1 被 l3,l4,l5;所截得的线段不相等,上面的结论能进一步推广吗?
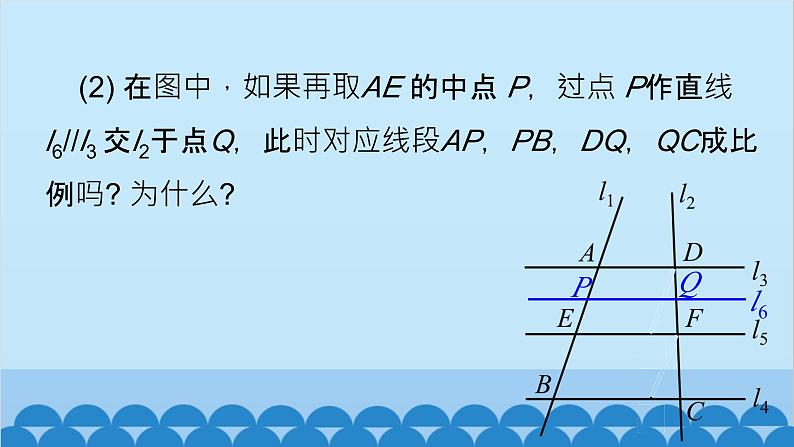
(2) 在图中,如果再取AE 的中点 P,过点 P作直线 l6//l3 交l2于点Q,此时对应线段AP,PB,DQ,QC成比例吗? 为什么?
如果取EB的中点 P1,过点 P1 作直线 l1//l2,交l2于点Q1(图1-5②).你发现 l1,l2,被平行线 l3,l7,l4截得的对应线段AP1,P1B,DQ1,Q1C 成比例吗(图1-5②)?
(3) 在图①中,再继续取 AP 的中点P2,或PE的中点P3,或PB的中点 P4,或 AP4的中点 P5,分别过这些点作 l3 的平行线,重复 (2)中的推理过程,还可得到
在本书中,把下面的命题作为第9个基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
(6) 特别地,在△ABC中,DE//BC线段AD,AB,AE,AC成比例吗?线段AD,AB,DE,BC呢?
于是,就得到基本事实9的一个推论:
推论 平行于三角形的一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
1. 如图,已知直线 l1//l2//l3,AB=3 cm,BC=5 cm,DE=2.4 cm,求DF的长.
2. 如图,已知直线 l1//l2//l3,直线 l4,l5分别与l1,l2,l3相交,直线l4与l5相交于点A,如图①②③.分别写出图中对应线段的比例式.
(1) 相似三角形是最简单、最常见的相似多边形你能根据相似多边形的定义说出两个怎样的三角形是相似三角形吗?怎样判定两个三角形是相似三角形呢?
利用定义判定两个三角形相似太不方便了。能否适当减少其中的某些条件,建立简便一些的判定方法呢?
(2) 我们知道,两个三角形有6 对元素,只要其中的3 对元素符合下面的种情况,就可以判定这两个三角形全等:
①两角及其夹边分别相等;②两角及其中一组等角的对边分别相等;③两边其夹角分别相等;④三边分别相等.
在①和②两种情况中,都包含三个条件:两角相等及其中某一边分别相等,由于相似三角形对应边的长可以不相等,如果把其中一边相等的条件去掉,仅保留两角分别相等的条件,能判定这两个三角形相似吗?
(3) 任意画△ABC,然后再作一个△A′B′C′,使∠A=∠A′,∠B=∠B′ (图1-9),观察这两个三角形,它们的形状相同吗?怎样判定它们相似呢?
如果将△A′B′C′放到 △ABC上面,使A′与A重合. A′B′落到AB上,由∠A=∠A′,那么A′C′落到AC上. 因为∠B=∠B′,所以 B′C′//BC,于是△ABC与△A′B′C′的三边对应成比例,且∠C=∠C′,所以△ABC∽△A′B′C′.
(4) 小莹利用实验的方法探索发现了命题“两角分别相等的三角形是相似三角形”.你能在她的思路的基础上,完成这一命题的证明吗?
*证明 在AB边(当AB<A′B′时,在其延长线)上截取AD=A′B′,过点D作DE//BC,交AC于点E. 则∠ADE =∠B,∠AED =∠C.
在△ADE和△A′B′C′中, ∵AD=AB,∠A=∠A′又∵∠B=∠B′, ∴∠ADE=∠B′. ∴ △ADE ≌△A′B′C′(ASA) ∴ ∠AED=∠C′,∠C=∠C′.
相似三角形的判定定理1 两角分别相等的两个三角形相似
如图,已知点 B,D 分别是∠A的两边AC,AE 上的点,连接BE,CD,相交于点O,如果∠1=∠2,图中有哪几对相似三角形?说明理由.
解:△DOE∽△BOC,△ABE∽△ADC.
理由是:因为∠1=∠2,∠DOE =∠BOC,由判定定理1,所以△DOE∽△BOC.同理,由∠E=∠C,∠A=∠A,所以 △ABE∽△ADC.
如图. B,C 分别是∠A两边上的任意一点. 过点B作BD⊥AC,垂足为点D. 过点C作CE⊥AB,垂足为点E. BD,CE 相交于点F. 图中共有哪几对相似三角形?说明理由.
图中的相似三角形有 6 对:△ABD∽△ACE,△ABD∽△FBE,△ABD∽△FCD,△FBE∽△ACE,△FBE∽△FCD,△ACE∽△FCD.
1. 在△ABC和△A′B′C′中,∠A=68°,∠B=40°,∠A′=68°,∠C′=72°,△ABC和△A′B′C′是否相似? 为什么?
2. 如图,CD是Rt△ABC的斜边AB上的高. (1)△ABC与△ACD相似吗? 为什么?
(2) 图中还有哪几对相似三角形?说明理由
(1) 我们知道,两边及其夹角分别相等的两个三角形全等.如果把其中两边相等的条件改为:“两个三角形的两边成比例”,保留“夹角相等”的条件,这两个三角形相似吗?
由已知∠A=∠A′,能仿照判定定理1的证明思路,在△ABC上截得一个与△A′B′C′全等且与△ABC相似的三角形吗?
证明:如图,在AB(或它的延长线)上截取 AD =A′B′,过点D作DE//BC,交 AC于点E. 于是
相似三角形的判定定理2 两边成比例,且夹角相等的两个三角形相似.
如图,AD=3,AE=4,BE=5,CD=9. △ADE与△ABC相似吗? 说明理由.
如图,ABCD,CDEF,EFGH是三个相连的正方形,连接AC,AF,AG . 你能证明∠FAC=∠AGC 吗? 试一试.
1. 选择题:如图,△ACD与△ABC相似的条件是 ( )(A) AC∶CD =AB∶BC(B) CD∶AD =AB∶AC(C) AC2 =AD·AB(D) CD′=AD·DB
(1) 我们知道,三边分别相等的两个三角形全等.如果把条件“三边相等’改为“三条边成比例”,这两个三角形相似吗?
与证明相似三角形的判定定理 1,2 类似,如果能在△ABC中用平行于BC边的直线截得一个△ADE,使它与△A′B′C′全等,并与△ABC相似,问题就可以解决.
*证明: 如图,在 AB(或它的延长线) 上截取 AD=A′B′ 过点D作 DE//BC,交AC于点E. 于是
∴ AE = A′C′,DE = B′C′,∴ △ADE ≌ △A′B′C′(SSS)∴ ∠A =∠A′.∴ △ABC ∽ △A′B′C′ (相似三角形的判定定理2).
相似三角形的判定定理3 三边成比例的两个三角形相似.
(1) 如果两个三角形的三条边的比都是 3∶4∶5,这两个三角形相似吗?
(2) 在什么条件下两个等腰三角形相似?在什么条件下两个直角三角形相似?
顶角相等的两个等腰三角形相似,底角相等的两个等腰三角形相似,腰和底边对应成比例的两个等腰三角形相似. 有一个锐角相等的两个直角三角形相似两直角边对应成比例的两个直角三角形相似,斜边和一条直角边对应成比例的两个直角三角形相似.
1. 在如图所示的正方形网格中,各画有一个格点三角形.找出其中的相似三角形.
图①中的格点三角形与图③中的格点三角形相似.
2. 已知三角形三边的长分别为 4,5,6,画出与它相似 的另一个三角形,使它的一条边长为2.你能画出几种 符合要求的三角形?与同学交流.
如图 ,为了测量一座水塔的高度,在阳光下,小亮走进水塔的影子里,使自己的影子刚好被水塔的影子遮住. 已知小亮的身高 BC=1.6 m此时,他的影子的长 AC=1m,他距水塔的底部E处11.5 m,水塔的顶部为点D. 根据以上数据,你能算出水塔的高度DE是多少吗?
按照例4的方法,你会测量教室附近一根电线杆的高度吗?与同学一起试一试.
小亮在测量一根电线杆的高度时,恰逢阴天,物体没有影子,于是他设计了测量电线杆高度的另一种方案:先在地面的适当位置平放一面小镜子,然后他看着镜子中电线杆的像,沿着电线杆的底部与镜子所在的直线一步步向后退,一直退到在镜子中刚好能看到电线杆的顶端为止.
这时分别量出他到镜子以及镜子到电线杆底部的距离和他的眼睛到地面的距离,就可算出电线杆的高. 你认为小亮的这个方案是否可行?它的原理是什么?
小亮的这个方案可行,它的原理是“反射角等于入射角”的光学原理.
如果认为可行,请用这种方法测出你们学校某幢建筑物的高度.
太阳给人类和自然界的生存与延续提供了宝贵的能源. 太阳离地球究竟有多远?自古以来,人们就在寻找这一问题的答案. 在我国,约公元前1世纪成书的《周算经》中有陈子测日的记载.陈子是公元前 6-7世纪人,与测量金字塔
高度的古希腊人泰勒斯是同一时期的人.他采用的方法如下: 如图,S表示太阳,C 是太阳正下方的点,在夏至时,分别在D,E两处立杆(即“牌”) AD和FE、BD和GE分别是杆 AD,
这一测量公式当初是怎样推出的,后人颇多探讨,并无定论.但我们可以用相似三角形对应边成比例的原理加以解释.
1. 如图,小亮要测量河流两岸 A,B 两点间的距离.他先从 B处出发,沿与AB成90°角的方向向前走 50 m到C处,立一竹竿,然后继续按这个方向朝前走 10 m到D处转90°,沿DE方向再到E处,使A(目标),C (竹竿)与E在同一条直线上,量得 DE=17m,利用以上数据,他是怎样求出A,B两点间距离的呢?
2. 在第 1 题中,除了小亮设计的方案外,你还能利用相 似三角形的知识,设计出另外的方案吗?
1.如图,已知DE//BC,DF//AC.指出与△ADE相似的三角形,并说明理由.
解:△ADE∽△ABC∽△DBF.
理由如下: ∵DE//BC, ∴∠ADE=∠B. ∵∠A=∠A, ∴△ADE∽△ABC.同理:△DBF∽△ABC. ∴△ADE∽△ABC∽△DBF.
2. 已知△ABC∽△A1B1C1 (1)如果△A1B1C1≌△A2B2C2 ,那么△A1B1C1与△A2B2C2相似吗? 为什么?
∵△ABC ∽ △A1B1C1,∴∠A =∠A1,∠B =∠B1.∵△A1B1C1 ≌ △A2B2C2,∴ ∠A1= ∠A2,∠B1= ∠B2.∴ ∠A = ∠A2.∠B = ∠B2,∴ △ABC ∽ △A2B2C2.
(2) 如果△A1B1C1 ∽ △A2B2C2 ,那么△ABC与△A2B2C2 相似吗? 为什么?
∵△ ABC ∽ △A1B1C1,∴∠A =∠A1,∠B =∠B1.∵△A1B1C1 ∽ △A2B2C2,∴ ∠A1= ∠A2,∠B1= ∠B2.∴ ∠A = ∠A2.∠B = ∠B2,∴ △ABC ∽ △A2B2C2.
3. 如图,已知 EF//CD//AB,EA//FB. (1) 写出所有与△ECG相似的三角形;
△BDG,△EAB,△BFE
4. 如图,AE与BD相交于点C,∠DME=∠A=∠B,且DM交AC于点F,ME交BC于点G.写出图中三对相似三角形,并选任一对说明其相似的理由.
解:△EAM∽△EMF,△DBM∽△DMG, △AFM∽△BMG (答案不唯一)
6. 在△ABC与△DEF中,已知∠B=∠E,且AB·EF=DE·BC,这两个三角形相似吗?为什么?
7.如图,在△ABC中,已知AE=2,BE=3,DB=AE,BC=7.5 . (1) △ABC∽△DBE吗? 为什么?
(2) 如果 DE=2.5,那么AC的长是多少?
8. 在△ABC与△A′B′C′中,已知AB=c,BC=a,CA=b,B′C′=a′,C′A′=b′,并且 a∶a′=b∶b′. 当A′B′为多少时(用a,a′,c或 b,b′,c 表示),△ABC与△A′B′C′相似?
9. 大刚的身高为 1.7 m,测得他站立在阳光下的影子长为 0.85 m,他把一只手臂竖直向上举起,测得影子长为1.1 m,大刚举起手臂超过头顶多少米?
10. 如图,在△ABC中,已知D是边AB上的一点,连接CD,那么还需要增加一个什么条件,才能使△ACD ∽ △ABC ?
11. 如图,在△ABC中,点D在边BC上, ∠BAC =∠ADC,AC=8,BC=16, 求CD的长.
解:在△ABC与△DAC中, ∠C为公共角, ∠BAC =∠ADC, 由相似三角形的判定定理1,得△ABC ∽△DAC,
12. P是Rt△ABC的斜边AB上异于A,B的一点,过点P作 直线截△ABC,使截得的三角形与△ABC相似,满足 这样条件的直线有几条?画出图形,并说明理由.
初中数学青岛版九年级上册第1章 图形的相似1.2 怎样判定三角形相似教课内容课件ppt: 这是一份初中数学青岛版九年级上册第1章 图形的相似1.2 怎样判定三角形相似教课内容课件ppt,共14页。PPT课件主要包含了巩固练习一,教材P14练习1,巩固练习二,拓展延伸等内容,欢迎下载使用。
2020-2021学年1.2 怎样判定三角形相似备课ppt课件: 这是一份2020-2021学年1.2 怎样判定三角形相似备课ppt课件,共22页。PPT课件主要包含了学习目标,复习引入,导入新课,合作探究,讲授新课,符号语言,典例精析,练一练,随堂练习,答案不相似等内容,欢迎下载使用。
青岛版九年级上册1.2 怎样判定三角形相似课文内容课件ppt: 这是一份青岛版九年级上册1.2 怎样判定三角形相似课文内容课件ppt,共21页。PPT课件主要包含了学习目标,不相似,观察与思考,导入新课,合作探究,讲授新课,符号语言,典例精析,练一练,随堂练习等内容,欢迎下载使用。













