初中数学北师大版九年级上册第二章 一元二次方程5 一元二次方程的根与系数的关系集体备课课件ppt

这是一份初中数学北师大版九年级上册第二章 一元二次方程5 一元二次方程的根与系数的关系集体备课课件ppt，共19页。PPT课件主要包含了知识回顾，学习目标，课堂导入，计算填表，x2-2x+10，新知探究，x1+x2，x1x2，∴方程有两个实数根，随堂练习等内容，欢迎下载使用。
1. 一元二次方程的一般形式？
ax2 + bx + c = 0 ( a≠0 )
2.一元二次方程有实数根的条件是什么？
△ = b2-4ac ≥ 0
3. 当△＞0，△=0，△＜0 根的情况如何？
△ > 0 时，方程有两个不相等的实数根；
△ = 0 时，方程有两个相等的实数根；
△ < 0 时，方程没有实数根；
4. 一元二次方程的求根公式是什么？
1.了解一元二次方程的根与系数的关系.
2.不解方程利用一元二次方程的根与系数的关系解决问题.
同学们，我们来做一个游戏，看谁能更快速的说出下列一元二次方程的两根和与两根积？ 
（1）x2-2x+1=0 （2）x2 - x-1=0  （3） 2x2-3x +1=0
x2 - x-1=0 
2x2-3x +1=0
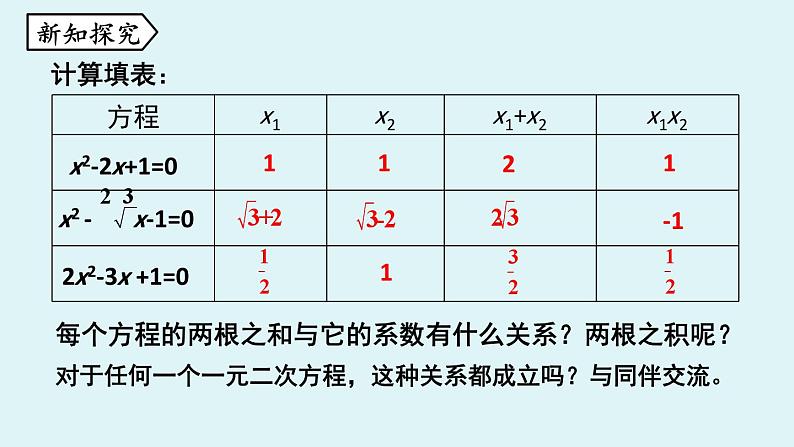
每个方程的两根之和与它的系数有什么关系？两根之积呢？
对于任何一个一元二次方程，这种关系都成立吗？与同伴交流。
一元二次方程 ax2+bx+c=0（a≠0）当b2-4ac ≥ 0 时有两个根：
如果方程 ax2+bx+c=0（a≠0）有两根实数根x1，x2，那么
例1 利用根与系数的关系，求下列方程的两根之和、两根之积：（1）x2 +7x +6 = 0 ; （2）2x2 - 3x -2 = 0 .
解： （1）这里 a = 1，b = 7，c = 6.
△ =b2-4ac = 72+4×1×6 = 49-24 = 25 > 0，
设方程的两个实数根是x1，x2，那么
x1+x2=-7， x1x2 = 6.
（2）这里 a = 2，b = -3，c = -2.
△ =b2-4ac = (-3)2-4×2×(-2) = 9+16 = 25 > 0，
x1+x2= ， x1x2 = -1.
(教材P50随堂练习）利用根与系数的关系，求下列方程的两根之和、两根之积： （1）x2-3x-1=0； （2）3x2+2x-5=0.
解：（1）x1+x2=3， x1x2 = -1.
（2）x1+x2= ， x1x2 = .
2. （教材P50随堂练习）小明和小华分别求出了方程 9x2+6x-1=0 的根.小明：x1 = x2 = ；小华：x1 = ，x2 = .他们的答案正确吗？说说你的判断方法.
小明和小华求得的根与算式都不符合，
∴小明和小华的答案都不正确.
3. （教材P50随堂练习）已知方程 x2- x-7=0 的一个根是 3 ，求它的另一个根.
解：因为x1x2 = -7.
所以x2 = .
4.（教材P51习题2.8第1题）利用根与系数的关系，求下列方程的两根之和、两根之积： （1）x(3x - 1)-1= 0； （2）(2x + 5) (x+1)= x + 7.
解：（1）3x2-x-1=0.
x1+x2= ，x1x2 = .
（2）x2+3x-1=0.
x1+x2= -3，x1x2 = -1 .
5. （教材P51习题2.8第2题）解下列方程： （1）12x2+7x+1 = 0； （2）0.8x2 + x = 0.3. （3）3x2+1= x； （4）(x+1)(x-3) = 2x+5.
（4）x2-4x-8=0，
（3）3x2- x+1=0，
6. （教材第51习题2.8第3题）已知方程 5x2+kx-6 = 0 的一个根是 2，求它的另一个根及 k 的值.
∵ x1= 2，∴x2 = ，
7. （教材P51习题2.8第4题）如果一个三角形两边的长分别等于一元二次方程x2-17x+66 = 0 的两个实数根，那么这个三角形的第三边的长可能是 20 吗？为什么？
解：由题意，可得 x1+x2 = 17，即两边长之和为 17，小于 20，所以这个三角形的第三边的长不可能是 20.