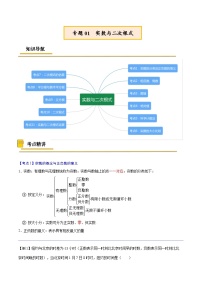
中考数学二轮复习专题01实数与二次根式含解析答案

这是一份中考数学二轮复习专题01实数与二次根式含解析答案，共18页。试卷主要包含了纽约与北京的时差为﹣13小时，下列实数中是无理数的是，下列各数是有理数的是，-2021的相反数是等内容，欢迎下载使用。


1．纽约与北京的时差为﹣13小时（正数表示同一时刻比北京时间早的时数，负数表示同一时刻比北京时间晚的时数），当北京时间1月7日8时时，纽约的时间是（ ）
A．1月6日21时B．1月7日21时C．1月6日19时D．1月6日20时
2．下列实数中是无理数的是（ ）
A．3.14B．C．D．
3．若盈余2万元记作万元，则万元表示（ ）
A．盈余2万元B．亏损2万元C．亏损万元D．不盈余也不亏损
4．下列各数是有理数的是（ ）
A．B．C．D．
5．-2021的相反数是（ ）
A．2021B．-2021C．D．
6．若，则实数在数轴上对应的点的位置是（ ）．
A．B．
C．D．
7．实数，在数轴上的位置如图所示，则下列式子正确的是（ ）
A．B．C．D．
8．实数在数轴上的对应点的位置如图所示，下列结论中正确的是（ ）
A．B．C．D．
9．如图，数轴上点A，B，C对应的有理数分别为，，，则下列结论中，正确的有（）
① ② ③ ④
A．1个B．2个
C．3个D．4个
10．有理数，在数轴上的对应点的位置如图所示，把按照从小到大的顺序排列，正确的是（ ）
A．B．
C．D．
11．的绝对值是（ ）
A．B．C．D．
12．的绝对值是（ ）
A．B．2021C．D．
13．据国家卫生健康委员会发布，截至2021年5月23日，31个省（区、市）及新疆生产建设兵团累计报告接种新冠病毒疫苗51085.8万剂次，将“51085.8万”用科学记数法表示为（ ）
A．B．C．D．
14．据交通运输部报道，截至2020年底，全国共有城市新能源公交车46.61万辆，位居全球第一．将46.61万用科学记数法表示为，则n等于（ ）
A．6B．5C．4D．3
15．我国是世界上免费为国民接种新冠疫苗最多的国家，截至2021年6月5日，免费接种数量已超过700000000剂次，将700000000用科学记数法表示为（ ）
A．B．C．D．
16．2021年2月25日，全国脱贫攻坚总结表彰大会在京举行，习近平总书记在大会上庄严宣告：“我国脱贫攻坚战取得了全面胜利．这是中国人民的伟大光荣，是中国共产党的伟大光荣，是中华民族的伟大光荣!”现行标准下9899万农村贫困人口全部脱贫，创造了又一个彪炳史册的人间奇迹．98990000用科学记数法表示为（ ）．
A．B．C．D．
17．若，则的大小关系是 ( )
A．B．C．D．
18．在实数3，，0，中，最大的数为（ ）
A．3B．C．0D．
19．下列各数中最大的是（ ）
A．B．C．0D．1
20．实数在数轴上的对应点可能是（ ）
A．点B．点C．点D．点
21．实数2介于（ ）
A．4和5之间B．5和6之间C．6和7之间D．7和8之间
22．4的算术平方根是（ ）
A．-2B．2C．D．
23．下列二次根式中，与是同类二次根式的是（ ）
A．B．C．D．
24．下列各式是最简二次根式的是（ ）
A．B．C．D．
25．将化为最简二次根式，其结果是（ ）
A．B．C．D．
26．是某三角形三边的长，则等于（ ）
A．B．C．10D．4
27．下列等式成立的是（ ）
A．B．C．D．
28．计算的结果正确的是（ ）．
A．1B．C．5D．9
29．的相反数是 ，倒数是 ．
30．已知（x-3）2+│2x-3y-3│=0，则y= ．
31．已知互为相反数，则=
32．比较大小： （填写“＞”或“＜”或“＝”）．
33．2021年5月7日，《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果．祖冲之是我国南北朝时期杰出的数学家，他是第一个将圆周率精确到小数点后第七位的人，他给出的两个分数形式：（约率）和（密率）．同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法，其理论依据是：设实数的不足近似值和过剩近似值分别为和（即有，其中，，，为正整数），则是的更为精确的近似值．例如：已知，则利用一次“调日法”后可得到的一个更为精确的近似分数为：；由于，再由，可以再次使用“调日法”得到的更为精确的近似分数……现已知，则使用两次“调日法”可得到的近似分数为 ．
34．9的平方根是 ．
35．
36．实数8的立方根是 ．
37．使在实数范围内有意义的的取值范围是 ．
38．使在实数范围内有意义的的取值范围是 ．
39．计算：．
40．计算：．
41．计算：．
42．计算：．
43．计算：．
评卷人
得分
一、单选题
评卷人
得分
二、填空题
评卷人
得分
三、计算题
参考答案：
1．C
【分析】纽约与北京的时差为-13小时，表示纽约的时间比北京时间晚13个小时，比得北京时间1月7日8时晚13个小时的时间为1月6日19时，从而得出答案．
【详解】解：24﹣[8+（﹣13）]＝19，
故选：C．
【点睛】考查有理数的意义，具有相反意义的量一个用正数表示，则与之相反的量就用负数表示，理解有理数的意义是解决问题的关键．
2．C
【分析】根据算术平方根、无理数的定义即可得．
【详解】A、是有限小数，属于有理数，此项不符题意；
B、，是有理数，此项不符题意；
C、是无理数，此项符合题意；
D、是分数，属于有理数，此项不符题意；
故选：C．
【点睛】本题考查了算术平方根、无理数，熟记定义是解题关键．
3．B
【分析】根据正数和负数表示具有相反意义的量解答．
【详解】解：∵盈余2万元记作 +2 万元，
∴-2万元表示亏损2万元，
故选：B．
【点睛】本题考查了正数和负数的意义，熟练掌握正数与负数的意义是解题的关键．
4．D
【分析】利用有理数和无理数的定义判断即可．
【详解】解：四个选项的数中：，，是无理数， 0是有理数，
故选项D符合题意．
故选：D．
【点睛】此题考查了实数，熟练掌握有理数与无理数的定义是解本题的关键．
5．A
【分析】根据相反数的定义：只有符号不同的两个数互为相反数，即可得出答案．
【详解】解：-2021的相反数是：2021．
故选A．
【点睛】本题主要考查了相反数的定义，熟知定义是解题的关键．
6．A
【分析】首先根据a的值确定a的范围，再根据a的范围确定a在数轴上的位置．
【详解】解：∵
∴，
∴，
∴点A在数轴上的可能位置是：
，
故选：A．
【点睛】本题考查有理数与数轴，解题关键是确定负数的大致范围．
7．B
【分析】由数轴易得，然后问题可求解．
【详解】解：由数轴可得：，
∴，
∴正确的是B选项；
故选B．
【点睛】本题主要考查数轴、绝对值的意义及实数的运算，熟练掌握数轴、绝对值的意义及实数的运算是解题的关键．
8．B
【分析】由数轴及题意可得，依此可排除选项．
【详解】解：由数轴及题意可得：，
∴，
∴只有B选项正确，
故选B．
【点睛】本题主要考查实数的运算及数轴，熟练掌握实数的运算及数轴是解题的关键．
9．C
【分析】由数轴可知：-3＜a＜-2，-2＜b＜-1，0＜c＜1，然后对各式进行判断即可.
【详解】解：由数轴可知：-3＜a＜-2，-2＜b＜-1，0＜c＜1，
∴，，，，
故①错误，②③④正确，
故选C.
【点睛】本题考查了数轴、有理数的加减乘除运算，熟练掌握运算法则是解题关键.
10．C
【分析】根据相反数在数轴上关于原点对称，可以先将在数轴上表示出来，从而利用数轴比较大小即可.
【详解】由题意得各数在数轴上如图所示：
∴，
∴A、B、D选项错误，
故选：C.
【点睛】本题主要考查了有理数的大小比较，熟练掌握相关概念是解题关键.
11．A
【分析】利用绝对值的定义直接得出结果即可
【详解】解：的绝对值是：9
故选:A
【点睛】本题考查绝对值的定义，正确理解定义是关键，熟记负数的绝对值是它的相反数是重点
12．B
【分析】根据绝对值的定义即可得出答案．
【详解】解：的绝对值为2021，
故选B．
【点睛】本题考查了绝对值，解题的关键是掌握负数的绝对值等于它的相反数．
13．D
【分析】根据科学记数法的表示形式，其中，n为整数，一定要将题目中的“51085.8万”转化为数字510858000，即可将题目中的数据用科学记数法表示出来．
【详解】51085.8万=510858000 ，
故选：D．
【点睛】本题主要考查科学记数法的表示形式，科学记数法的表示形式，其中，n为整数，此题容易将题目中的“万”遗漏，掌握科学记数法的表示形式是解题关键．
14．B
【分析】把46.61万表示成科学记数法的形式，即可确定n ．
【详解】46.61万=466100=4.661 ，故n=5
故选：C．
【点睛】本题考查把一个绝对值较大的数用科学记数法表示，科学记数法的形式为，其中，n为绝对值较大的数的整数数位与1的差．
15．C
【分析】将700000000写成a×10n（1＜|a|＜10，n为正整数）的形式即可．
【详解】解：700000000=．
故选C．
【点睛】本题主要考查了运用科学记数法表示绝对值大于1的数，将原数写成a×10n（1＜|a|＜10，n为正整数）的形式，确定a、n的值成为解答本题的关键．
16．D
【分析】根据科学记数法的性质分析，即可得到答案．
【详解】98990000用科学记数法表示为：
故选：D．
【点睛】本题考查了科学记数法的知识；解题的关键是熟练掌握科学记数法的性质，从而完成求解．
17．B
【分析】根据时，可得越平方越小，，从而得到大小关系式．
【详解】
，
，，
，
故选：B．
【点睛】本题考查了简单的实数的比较，可利用特殊值法即可比较大小，也可利用当时，的指数越大则数值越小解题．
18．A
【分析】根据正数大于零，负数小于零，正数大于一切负数，两个负数比较大小，绝对值大的反而小，两个正数比较大小，绝对值大数就大，据此判断即可．
【详解】根据有理数的比较大小方法，可得：
，
因此最大的数是：3,
故选：A．
【点睛】本题考查了实数的比较大小，解答此题的关键在于明确：正数＞0＞负数．
19．D
【分析】把选项中的4个数按从小到大排列，即可得出最大的数．
【详解】由于－3<－2<0<1，则最大的数是1
故选：D．
【点睛】本题考查了有理数的大小比较，一般地，正数大于零，零大于负数，两个负数，绝对值大的反而小．
20．D
【分析】先求出的近似值，再判定它位于哪两个整数之间即可找出其对应点．
【详解】解：∵，
∴，
∴它表示的点应位于2和3之间，
所以对应点是点D，
故选：D．
【点睛】本题考查了对无理数的估值及其在数轴上的表示，解决本题的关键是能正确估出的整数部分，本题较基础，考查了学生的基本功．
21．C
【分析】首先化简＝，再估算，由此即可判定选项．
【详解】解：∵＝，且6＜＜7，
∴6＜＜7．
故选：C．
【点睛】本题考查估算实数大小，方法就是用有理数来逼近，求该数的近似值，一般情况下要牢记1到20整数的平方，可以快速准确地进行估算.
22．B
【详解】4的算术平方根是2．
故选B．
【点睛】本题考查求一个数的算术平方根．掌握算术平方根的定义是解题关键．
23．C
【分析】先把每个二次根式进行化简，化成最简二次根式，后比较被开方数即可．
【详解】A.与的被开方数不相同，故不是同类二次根式；
B.，与不是同类二次根式；
C.，与被开方数相同，故是同类二次根式；
D.，与被开方数不同，故不是同类二次根式．
故选：C．
【点睛】本题考查了二次根式的化简，同类二次根式，熟练掌握根式化简的基本方法，灵活运用同类二次根式的定义判断解题是求解的关键．
24．A
【分析】根据最简二次根式的定义即可求出答案．
【详解】解：A、是最简二次根式，故选项正确；
B、=，不是最简二次根式，故选项错误；
C、，不是最简二次根式，故选项错误；
D、，不是最简二次根式，故选项错误；
故选：A
【点睛】本题考查最简二次根式，解题的关键是正确理解最简二次根式的定义，本题属于基础题型．
25．D
【分析】根据二次根式的化简方法即可得．
【详解】解：原式，
，
故选：D．
【点睛】本题考查了二次根式的化简，熟练掌握化简方法是解题关键．
26．D
【分析】先根据三角形三边的关系求出的取值范围，再把二次根式进行化解，得出结论．
【详解】解：是三角形的三边，
，
解得：，
，
故选：D．
【点睛】本题考查了二次根式的性质及化简，解题的关键是：先根据题意求出的范围，再对二次根式化简．
27．D
【分析】根据二次根式的运算法则即可逐一判断．
【详解】解：A、3和不能合并，故A错误；
B、，故B错误；
C、，故C错误；
D、，正确；
故选：D．
【点睛】本题考查了二次根式的运算，解题的关键是掌握基本的运算法则．
28．A
【分析】利用二次根式的乘除法则计算即可得到结果．
【详解】解：
，
故选：A．
【点睛】本题主要考查了二次根式的乘除法，熟练掌握运算法则是解题的关键．
29．
【分析】根据相反数，倒数的概念可得结果.
【详解】解：的相反数是，倒数是.
故答案为：，.
【点睛】本题主要考查相反数，倒数的概念及性质．相反数的定义：只有符号不同的两个数互为相反数，0的相反数是0；倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．
30．1
【分析】由题干（x-3）2+│2x-3y-3│=0得到x，y的值即可．
【详解】由题干（x-3）2+│2x-3y-3│=0得：
且│2x-3y-3│=0，
∴，
解得： ，
故答案为：1．
【点睛】此题主要考查绝对值和完全平方的意义，难度一般．
31．—4
【分析】首先根据题意，得出，然后根据非负性，即可得出x和y的值，代入即可得解.
【详解】由已知得，
∴
解得
∴
【点睛】此题主要考查非负性的应用，熟练掌握，即可解题.
32．＞
【分析】直接用，结果大于0，则大；结果小于0，则大．
【详解】解：，
∴，
故答案为：＞．
【点睛】本题主要考查实数的大小比较，常用的比较大小的方法有作差法、作商法、平方法等，正确理解和记忆方法背后的知识点是解题关键．
33．
【分析】根据“调日法”的定义，第一次结果为：，近似值大于 ，所以，根据第二次“调日法”进行计算即可.
【详解】解：∵
∴第一次“调日法”，结果为：
∵
∴
∴第二次“调日法”，结果为：
故答案为：
【点睛】本题考查无理数的估算，根据定义，严格按照例题步骤解题是重点．
34．±3
【分析】根据平方根的定义解答即可．
【详解】解：∵（±3）2=9，
∴9的平方根是±3．
故答案为±3．
【点睛】本题考查了平方根的定义，注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．
35．
【分析】先算，再开根即可．
【详解】解：
故答案是：．
【点睛】本题考查了求一个数的4次方和对一个实数开根号，解题的关键是：掌握相关的运算法则．
36．2
【分析】根据立方根的概念解答．
【详解】∵，
∴8的立方根是2．
故答案为：2
【点睛】本题考查立方根的概念义，正确掌握立方根的概念是解题的关键．
37．
【分析】根据二次根式的被开方数是非负数，列出不等式，即可求解．
【详解】∵x-1≥0，
∴x≥1．
故答案是：．
【点睛】本题主要考查二次根式有意义的条件，掌握二次根式的被开方数是非负数，是解题的关键．
38．
【分析】根据二次根式的被开方数是非负数，列出不等式，即可求解．
【详解】∵x-1≥0，
∴x≥1．
故答案是：．
【点睛】本题主要考查二次根式有意义的条件，掌握二次根式的被开方数是非负数，是解题的关键．
39．-2
【分析】先分别计算出有理数的乘方及括号内的有理数加减，再计算乘除，即可求得结果．
【详解】解：
．
【点睛】此题考查了有理数的混合运算，熟练掌握有理数混合运算的运算顺序及相关运算法则是解答此题的关键．
40．
【分析】根据算术平方根的定义、零指数幂的意义、绝对值的意义、特殊角的三角函数值、实数的运算等知识即可完成本题的计算．
【详解】原式
【点睛】本题考查了算术平方根的定义、零指数幂的意义、绝对值的意义、特殊角的三角函数值、实数的运算等知识，关键是熟练掌握这些知识．
41．2．
【分析】根据负整数指数幂、0指数幂的运算法则及算术平方根的定义计算即可得答案．
【详解】
．
【点睛】本题考查实数的运算，熟练掌握负整数指数幂、0指数幂的运算法则及算术平方根的定义是解题关键．
42．
【分析】先运用绝对值、特殊角的三角函数值、负整数次幂以及平方根的知识化简，然后再计算即可．
【详解】解：
=
=．
【点睛】本题主要考查了绝对值、特殊角的三角函数值、负整数次幂、平方根等知识点，灵活应用相关知识成为解答本题的关键．
43．
【分析】直接利用零指数幂，二次根式分母有理化、负整数指数幂、特殊角的三角函数值计算即可．
【详解】解：
．
【点睛】本题考查了零指数幂，二次根式分母有理化、负整数指数幂、特殊角的三角函数值的运算法则，解题的关键是：掌握相关的运算法则．