
浙江省温州市苍南县六校联考2023-2024学年八年级上学期第一次月考数学试卷
展开这是一份浙江省温州市苍南县六校联考2023-2024学年八年级上学期第一次月考数学试卷,共28页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
1.如图,为了估计一池塘岸边两点A,B之间的距离,小颖同学在池塘一侧选取了一点P,测得PA=100m,PB=90m,那么点A与点B之间的距离可能是( )
A.10mB.120mC.190mD.220m
2.下面由北京冬奥会比赛项目图标组成的四个图形中,可看作轴对称图形的是( )
A.B.C.D.
3.若不等式﹣3x<1,两边同时除以﹣3,得( )
A.x>﹣B.x<﹣C.x>D.x<
4.将一副三角尺按如图的方式摆放,其中l1∥l2,则∠α的度数是( )
A.30°B.45°C.60°D.70°
5.如图,∠A=∠D=90°,AC=DE,使△ABC≌△DFE,需添加一个条件,下列所给的条件及相应的判定定理不正确的是( )
A.AB=DF(SAS)B.∠B=∠F(AAS)
C.BC=FE(SSA)D.∠ACB=∠DEF(ASA)
6.给出下列命题:①三角形任何两边之和大于第三边;②三角形任何一外角等于两内角之和;③两边和一角对应相等的两个三角形全等,下列属于真命题的是( )
A.①③B.②③C.①②D.①
7.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
A.AC=A′C′B.AB∥B′C′C.AA′⊥MND.BO=B′O
8.如图,∠BAC=100°,AB>AC.若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是( )
A.20°B.60°C.50°D.40°
9.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画弧MN,交OB于点C,连接CD.②以D为圆心,DO长为半径画弧GH,交OB于点E,连接DE.则∠CDE的度数为( )
A.25°B.30°C.35°D.40°
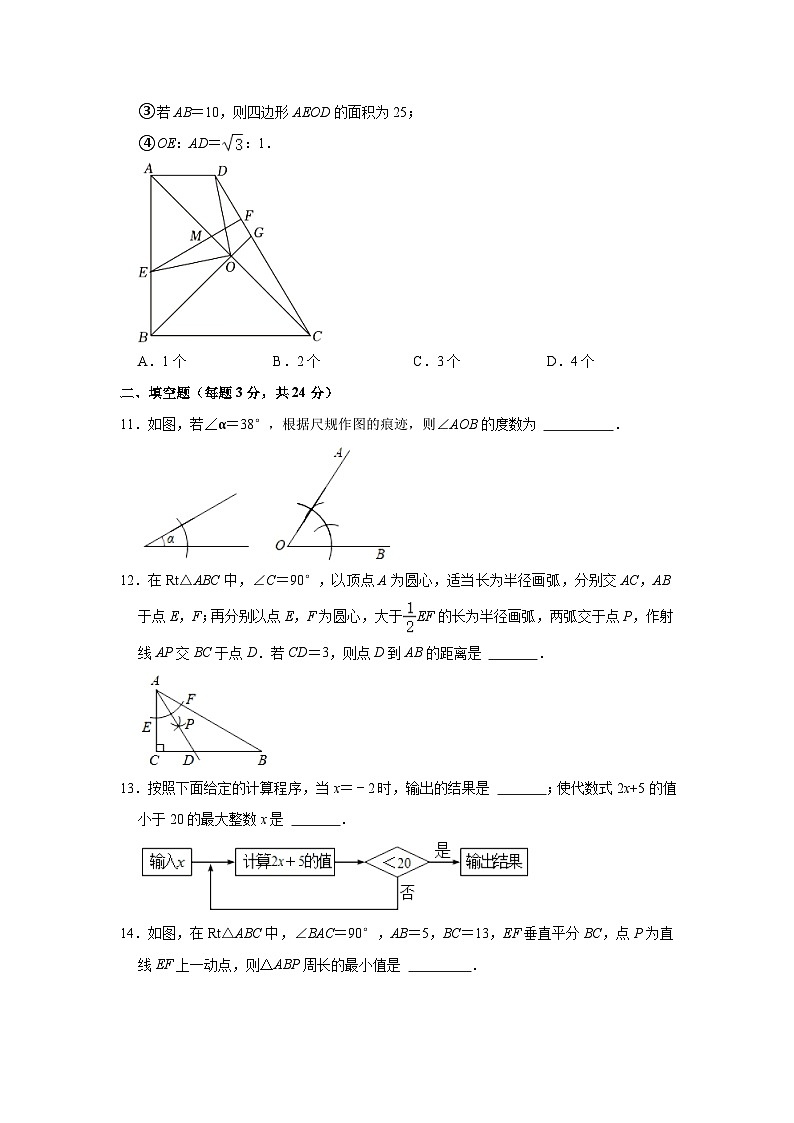
10.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC.O为AC中点,OE⊥OD交AB于点E,EF⊥CD于点F,交AC于点M,BO的延长线交DC于点G.若,则下列结论正确的( )
①OE=OD;
②BG=CM;
③若AB=10,则四边形AEOD的面积为25;
④OE:AD=:1.
A.1个B.2个C.3个D.4个
二、填空题(每题3分,共24分)
11.如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 .
12.在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点E,F;再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线AP交BC于点D.若CD=3,则点D到AB的距离是 .
13.按照下面给定的计算程序,当x=﹣2时,输出的结果是 ;使代数式2x+5的值小于20的最大整数x是 .
14.如图,在Rt△ABC中,∠BAC=90°,AB=5,BC=13,EF垂直平分BC,点P为直线EF上一动点,则△ABP周长的最小值是 .
15.直角三角形的周长为12cm,斜边长为5cm,则其面积是 cm2.
16.如图是长方形纸带a,∠DEF=20°,将纸带沿EF折叠成图b,则∠AEG的度数为 度,再沿BF折叠成图c,则图中的∠CFE的度数是 度.
17.在Rt△ABC中,AC=8,BC=6,∠C=90°.现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则DE的长为 .
18.如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,DC'与AB交于点E,连接AC′,若AD=AC′=2,BD=3,则点D到BC的距离为 .
三、解答题(共46分)
19.如图,在正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,请按要求完成下列问题(仅用无刻度的直尺作图,且保留必要的作图痕迹):
(1)在AB上找一点D,使CD⊥AB;
(2)在AC上找一点E,使BE平分∠ABC.
20.莆仙戏是现存最古老的地方戏剧种之一,被称为“宋元南戏的活化石”,2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”.该剧中“油纸伞”无疑是最重要的道具,依伞设戏,情节新颖,结构巧妙,谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌.“油纸伞”的制作工艺十分巧妙.如图,伞圈D沿着伞柄滑动时,总有伞骨BD=CD,AB=AC,从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC.为什么?
21.已知:如图,点B,E,F,C在同一条直线上,AB=DC,∠B=∠C,BE=CF.
(1)求证:△ABF≌△DCE.
(2)若∠AGE=80°,求∠AFE的度数.
22.如图,AD是△ABC的高,CE是△ACB的角平分线,F是AC中点,∠ACB=50°,∠BAD=70°.
(1)求∠AEC的度数;
(2)若△BCF与△BAF的周长差为3,AB=7,能否求出BC的值?若能,请写出理由和结果;若不能,请你补充条件并解答.
23.如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连接CD、DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
24.问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
参考答案
一、选择题(本题有10个小题,每小题3分,共30分)
1.如图,为了估计一池塘岸边两点A,B之间的距离,小颖同学在池塘一侧选取了一点P,测得PA=100m,PB=90m,那么点A与点B之间的距离可能是( )
A.10mB.120mC.190mD.220m
【分析】根据三角形两边之和大于第三边,两边之差小于第三边可以确定BC的取值范围,从而可以解答本题.
解:∵在△ABC中,PA=100m,PB=90m,
∴100﹣90<AB<100+90,
∴10<AB<190,
故点A与点B之间的距离可能是120m.
故选:B.
【点评】本题考查三角形三边关系,解题的关键是明确三角形两边之和大于第三边,两边之差小于第三边.
2.下面由北京冬奥会比赛项目图标组成的四个图形中,可看作轴对称图形的是( )
A.B.C.D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:选项A、B、C不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
选项D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:D.
【点评】此题主要考查了轴对称图形,掌握轴对称图形的定义是解答本题的关键.
3.若不等式﹣3x<1,两边同时除以﹣3,得( )
A.x>﹣B.x<﹣C.x>D.x<
【分析】利用不等式的性质解答即可.
解:不等式﹣3x<1,两边同时除以﹣3,得x>﹣.
故选:A.
【点评】本题主要考查了不等式的性质.解不等式依据不等式的性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.特别是在系数化为1这一个过程中要注意不等号的方向的变化.
4.将一副三角尺按如图的方式摆放,其中l1∥l2,则∠α的度数是( )
A.30°B.45°C.60°D.70°
【分析】依据平行线的性质,可得∠ABC,再根据∠CBD=90°,即可得到∠α=90°﹣30°=60°.
解:如图所示,∵l1∥l2,
∴∠A=∠ABC=30°,
又∵∠CBD=90°,
∴∠α=90°﹣30°=60°,
故选:C.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,内错角相等.
5.如图,∠A=∠D=90°,AC=DE,使△ABC≌△DFE,需添加一个条件,下列所给的条件及相应的判定定理不正确的是( )
A.AB=DF(SAS)B.∠B=∠F(AAS)
C.BC=FE(SSA)D.∠ACB=∠DEF(ASA)
【分析】根据全等三角形的判定定理逐个判断即可.
解:A.AB=DF,∠A=∠D=90°,AC=DE,符合全等三角形的判定定理SAS,能推出△ABC≌△DFE,故本选项不符合题意;
B.∠B=∠F,∠A=∠D,AC=DE,符合全等三角形的判定定理AAS,能推出△ABC≌△DFE,故本选项不符合题意;
C.∠A=∠D=90°,BC=FE,AC=DE,符合两直角三角形全等的判定定理HL(不是SSA),能推出△ABC≌△DFE,故本选项符合题意;
D.∠ACB=∠DEF,AC=DE,∠A=∠D,符合全等三角形的判定定理ASA,能推出△ABC≌△DFE,故本选项不符合题意;
故选:C.
【点评】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL等.
6.给出下列命题:①三角形任何两边之和大于第三边;②三角形任何一外角等于两内角之和;③两边和一角对应相等的两个三角形全等,下列属于真命题的是( )
A.①③B.②③C.①②D.①
【分析】利用三角形的三边关系、外角的性质、全等三角形的判定方法等知识分别判断后即可确定正确的选项.
解:①三角形任何两边之和大于第三边,正确,是真命题,符合题意;
②三角形任何一外角等于不相邻的两内角之和,故原命题错误,是假命题,不符合题意;
③两边和夹角对应相等的两个三角形全等,故原命题错误,是假命题,不符合题意.
真命题有①,
故选:D.
【点评】本题考查了命题与定理的知识,解题的关键是了解有关的定义及定理,难度不大.
7.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中不一定正确的是( )
A.AC=A′C′B.AB∥B′C′C.AA′⊥MND.BO=B′O
【分析】根据轴对称的性质对各选项分析判断后利用排除法求解.
解:∵△ABC与△A′B′C′关于直线MN对称,
∴AC=A′C′,AA′⊥MN,BO=B′O,故A、C、D选项正确,
AB∥B′C′不一定成立,故B选项错误,
所以,不一定正确的是B.
故选:B.
【点评】本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
8.如图,∠BAC=100°,AB>AC.若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是( )
A.20°B.60°C.50°D.40°
【分析】由AB=AC,∠BAC=100°,可求得∠B+∠C的度数,又由MP,NQ分别垂直平分AB,AC,根据线段垂直平分线的性质,可得AP=BP,AQ=CQ,继而求得∠BAP+∠CAQ的度数,则可求得答案.
解:∵AB=AC,∠BAC=100°,
∴∠B+∠C=180°﹣∠BAC=80°,
∵MP,NQ分别垂直平分AB,AC,
∴AP=BP,AQ=CQ,
∴∠BAP=∠B,∠CAQ=∠C,
∴∠BAP+∠CAQ=80°,
∴∠PAQ=∠BAC﹣(∠BAP+∠CAQ)=20°.
故选:A.
【点评】此题考查了线段垂直平分线的性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.
9.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画弧MN,交OB于点C,连接CD.②以D为圆心,DO长为半径画弧GH,交OB于点E,连接DE.则∠CDE的度数为( )
A.25°B.30°C.35°D.40°
【分析】由作图步骤①,可知OC=OD,利用等边对等角,可得出∠OCD=∠ODC,在△OCD中,利用三角形内角和定理,可求出∠OCD的度数,由作图步骤②,可知DO=DE,利用等边对等角,可求出∠DEO的度数,由∠OCD是△CDE的外角,再利用三角形的外角性质,即可求出∠CDE的度数.
解:由作图步骤①可知:OC=OD,
∴∠OCD=∠ODC.
在△OCD中,∠COD=40°,∠OCD=∠ODC,
∴∠OCD=(180°﹣∠COD)=×(180°﹣40°)=70°.
由作图步骤②可知:DO=DE,
∴∠DEO=∠DOE=40°.
∵∠OCD是△CDE的外角,
∴∠OCD=∠DEC+∠CDE,
∴∠CDE=∠OCD﹣∠DEC=70°﹣40°=30°.
故选:B.
【点评】本题考查了三角形内角和定理、等腰三角形的判定与性质以及三角形的外角性质,根据作图的步骤,找出OC=OD=DE是解题的关键.
10.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC.O为AC中点,OE⊥OD交AB于点E,EF⊥CD于点F,交AC于点M,BO的延长线交DC于点G.若,则下列结论正确的( )
①OE=OD;
②BG=CM;
③若AB=10,则四边形AEOD的面积为25;
④OE:AD=:1.
A.1个B.2个C.3个D.4个
【分析】先根据等腰直角三角形的性质和平行线的性质推导出∠OBE=∠OAD,OB=OA=OC=AC,∠BOE=∠AOD=90°﹣∠AOE,即可证明△BOE≌△AOD,得OE=OD,可判断①正确;
由∠DOG=∠EOM,∠ODG=90°﹣∠DIF=90°﹣∠OIE=∠OEM,OD=OE,可证明△ODG≌△OEM,得OG=OM,则OG+OB=OM+OC,所以BG=CM,可判断②正确,
由S四边形AEOD=S△AOE+S△AOD=S△AOE+S△BOE=S△AOB=S△ABC≠S△ABC,可判断③错误;
连接DE,设AD=BE=m,由=,可推导出AB=BC=3m,AE=AB﹣BE=2m,则2OE2=m2+(2m)2,得OE=m,所以=,可判断④正确,于是得到问题的答案.
解:∵AB=BC,∠ABC=90°,
∴∠BAC=∠BCA=45°,
∵AD∥BC,
∴∠OAD=∠BCA=45°,
∵O为AC中点,
∴BO⊥AC,∠OBE=∠OBC=∠ABC=45°,
∴∠OBE=∠OAD,OB=OA=OC=AC,
∵OE⊥OD,
∴∠AOB=∠DOE=∠AOG=90°,
∴∠BOE=∠AOD=90°﹣∠AOE,∠DOG=∠EOM=90°﹣∠AOD,
在△BOE和△AOD中,
,
∴△BOE≌△AOD(ASA),
∴OE=OD,BE=AD,
故①正确;
∵EF⊥CD于点F,
∴∠EFD=90°,
∵∠DIF=∠OIE,
∴∠ODG=90°﹣∠DIF=90°﹣∠OIE=∠OEM,
在△ODG和△OEM中,
,
∴△ODG≌△OEM(ASA),
∴OG=OM,
∴OG+OB=OM+OC,
∴BG=CM,
故②正确;
∵OA=OC,
∴S△AOB=S△COB=S△ABC,
∵S△AOD=S△BOE,
∴S四边形AEOD=S△AOE+S△AOD=S△AOE+S△BOE=S△AOB=S△ABC≠S△ABC,
故③错误;
连接DE,设AD=BE=m,
∵=,
∴AB=BC=3m,
∴AE=AB﹣BE=2m,
∵∠DOE=∠DAE=90°,OE=OD,
∴2OE2=OE2+OD2=AD2+AE2=DE2,
∴2OE2=m2+(2m)2,
∴OE=m,
∴==,
故④错误,
故选:B.
【点评】此题重点考查等腰直角三角形的判定与性质、同角的余角相等、全等三角形的判定与性质、直角三角形斜边上的中线等于斜边的一半、勾股定理等知识,正确地作出辅助线并且证明△BOE≌△AOD及△ODG≌△OEM是解题的关键.
二、填空题(每题3分,共24分)
11.如图,若∠α=38°,根据尺规作图的痕迹,则∠AOB的度数为 76° .
【分析】由尺规作图的作法得到∠AOB=2∠α,代入数据即可得到答案.
解:由尺规作图可知,∠AOB=2∠α,
∵∠α=38°,
∴∠AOB=76°,
故答案为:76°.
【点评】本题考查了作图﹣基本作图,熟练掌握基本作图的方法是解题的关键.
12.在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点E,F;再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线AP交BC于点D.若CD=3,则点D到AB的距离是 3 .
【分析】作DM⊥AB于点M,由作图知AD平分∠BAC且CD=3,根据角平分线上的点到角两边的距离相等得出DM=DC=3.
解:如图所示,过点D作DM⊥AB于点M,
由作图知AD平分∠BAC,且CD=3,
∴DM=DC=3,
故答案为:3.
【点评】本题主要考查作图—基本作图,解题的关键是掌握角平分线的尺规作图和角平分线的性质.
13.按照下面给定的计算程序,当x=﹣2时,输出的结果是 1 ;使代数式2x+5的值小于20的最大整数x是 7 .
【分析】由运算程序可计算出当x=2时,输出结果,求得使代数式2x+5的值小于20的最大整数x是7.
解:当x=﹣2时,第1次运算结果为2×(﹣2)+5=1,
∴当x=﹣2时,输出结果是1,
使代数式2x+5的值小于20的最大整数x是7,
故答案为:1,7.
【点评】本题考查了一元一次不等式的应用以及有理数的混合运算,能够理解题意是解题的关键.
14.如图,在Rt△ABC中,∠BAC=90°,AB=5,BC=13,EF垂直平分BC,点P为直线EF上一动点,则△ABP周长的最小值是 17 .
【分析】连接PC,如图,先由勾股定理得AC的长,再根据线段垂直平分线的性质得到PB=PC,则PA+PB=PA+PC,根据三角形三边之间的关系得到PA+PC≥AC(当且仅当A、P、C共线时取等号),则PA+PC的最小值为AC的长,所以△ABP周长的最小值=AB+AC.
解:连接PC,如图,
在Rt△ABC中,∠BAC=90°,AB=5,BC=13,
∴AC==12,
∵EF垂直平分BC,
∴PB=PC,
∴PA+PB=PA+PC,
∵PA+PC≥AC(当且仅当A、P、C共线时取等号),
∴PA+PC的最小值为AC的长,
∴△ABP周长的最小值=AB+AC=5+12=17.
故答案为:17.
【点评】此题考查的是轴对称﹣最短线路问题、线段垂直平分线的性质,正确作出辅助线是解决此题的关键.
15.直角三角形的周长为12cm,斜边长为5cm,则其面积是 6 cm2.
【分析】根据周长列出关于另外两直角边的关系,再利用勾股定理列出另一关系,联立即可解得两直角边之积,再进行面积的计算.
解:设另外两直角边分别为x,y.
则x+y+5=12 ①
x2+y2=25②
①②联立解得xy=12,
故直角三角形的面积为.
【点评】考查根据已知条件列方程的能力,并与直角三角形的面积结合起来进行简单应用.注意不需要解出两直角边的长.
16.如图是长方形纸带a,∠DEF=20°,将纸带沿EF折叠成图b,则∠AEG的度数为 140 度,再沿BF折叠成图c,则图中的∠CFE的度数是 120 度.
【分析】由折叠知∠DEF=∠GEF=20°,根据平行线的性质可得∠AEF+∠GFE=180°,然后再求∠CFE的度数.
解:∵∠DEF=20°,
∴∠FEG=20°,
∴∠AEG=180°﹣20°﹣20°=140°,
∵AE∥BF,
∴∠AEF+∠GFE=180°,
∵∠AEF=180°﹣20°=160°,
∴∠GFE=20°,
∴∠CFE=180°﹣20°×3=120°,
故答案为:140;120.
【点评】此题主要考查了平行线的性质和图形的折叠,关键是掌握两直线平行,同旁内角互补,折叠前后角的度数不变.
17.在Rt△ABC中,AC=8,BC=6,∠C=90°.现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则DE的长为 .
【分析】根据勾股定理可求AB=10,由折叠的性质可得BE=AE,AD=BD=5,DE⊥AB,根据勾股定理可求BE的长,DE的长.
解:∵∠C=90°,AC=8,BC=6,
∴AB==10,
∵将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,
∴BE=AE,AD=BD=5,DE⊥AB,
在Rt△BEC中,BE2=BC2+CE2,
∴BE2=36+(8﹣BE)2,
∴BE=,
在Rt△BDE中,DE==,
故答案为:.
【点评】本题考查了翻折变换,勾股定理,熟练运用折叠的性质是本题的关键.
18.如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,DC'与AB交于点E,连接AC′,若AD=AC′=2,BD=3,则点D到BC的距离为 .
【分析】连接CC',交BD于点M,过点D作DH⊥BC'于点H,由翻折知,△BDC≌△BDC',BD垂直平分CC',证△ADC'为等边三角形,利用解直角三角形求出DM=1,C'M=DM=,BM=2,在Rt△BMC'中,利用勾股定理求出BC'的长,在△BDC'中利用面积法求出DH的长,则可得出答案.
解:如图,连接CC',交BD于点M,过点D作DH⊥BC'于点H,
∵AD=AC′=2,D是AC边上的中点,
∴DC=AD=2,
由翻折知,△BDC≌△BDC',BD垂直平分CC',
∴DC=DC'=2,BC=BC',CM=C'M,
∴AD=AC′=DC'=2,
∴△ADC'为等边三角形,
∴∠ADC'=∠AC'D=∠C'AC=60°,
∵DC=DC',
∴∠DCC'=∠DC'C=×60°=30°,
在Rt△C'DM中,
∠DC'C=30°,DC'=2,
∴DM=1,C'M=DM=,
∴BM=BD﹣DM=3﹣1=2,
在Rt△BMC'中,
BC'===,
∵S△BDC'=BC'•DH=BD•CM,
∴DH=3×,
∴DH=,
∵∠DCB=∠DBC',
∴点D到BC的距离为.
故答案为:.
【点评】本题考查了轴对称的性质,解直角三角形,勾股定理等,解题关键是会通过面积法求线段的长度.
三、解答题(共46分)
19.如图,在正方形网格中,每个小正方形的边长都为1,△ABC的三个顶点均在格点上,请按要求完成下列问题(仅用无刻度的直尺作图,且保留必要的作图痕迹):
(1)在AB上找一点D,使CD⊥AB;
(2)在AC上找一点E,使BE平分∠ABC.
【分析】(1)取格点T,连接CT交AB于点D,点D即为所求;
(2)取格点P,连接AP,取AP的中点Q,连接BQ交AC于点E,点E即为所求.
【解答】解;(1)如图,点D即为所求;
(2)如图,点E即为所求.
【点评】本题考查作图﹣应用与设计作图,三角形的高,角平分线等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
20.莆仙戏是现存最古老的地方戏剧种之一,被称为“宋元南戏的活化石”,2021年5月莆仙戏《踏伞行》获评为“2020年度国家舞台艺术精品创作扶持工程重点扶持剧目”.该剧中“油纸伞”无疑是最重要的道具,依伞设戏,情节新颖,结构巧妙,谱写了一曲美轮美奂、诗意盎然的传统戏曲乐歌.“油纸伞”的制作工艺十分巧妙.如图,伞圈D沿着伞柄滑动时,总有伞骨BD=CD,AB=AC,从而使得伞柄AP始终平分同一平面内两条伞骨所成的∠BAC.为什么?
【分析】直接利用全等三角形的判定方法得出△ABD≌△ACD(SSS),进而得出答案.
解:AP始终平分同一平面内两条伞骨所成的∠BAC,
理由:在△ABD和△ACD中
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
即AP平分∠BAC.
【点评】此题主要考查了全等三角形的应用,正确得出△ABD≌△ACD是解题关键.
21.已知:如图,点B,E,F,C在同一条直线上,AB=DC,∠B=∠C,BE=CF.
(1)求证:△ABF≌△DCE.
(2)若∠AGE=80°,求∠AFE的度数.
【分析】(1)由BE=CF,两边加上EF,得到BF=CE,利用SAS即可得证.
(2)根据全等三角形的性质和三角形内角和定理解答即可.
【解答】(1)证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS);
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴GE=GF,
∵∠AGE=80°,
∴∠EGF=180°﹣80°=100°,
∴∠AFE==40°.
【点评】此题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定方法是解本题的关键.
22.如图,AD是△ABC的高,CE是△ACB的角平分线,F是AC中点,∠ACB=50°,∠BAD=70°.
(1)求∠AEC的度数;
(2)若△BCF与△BAF的周长差为3,AB=7,能否求出BC的值?若能,请写出理由和结果;若不能,请你补充条件并解答.
【分析】(1)根据直角三角形的性质求出∠ABC,根据角平分线的定义求出∠ECB,再根据三角形的外角性质计算即可;
(2)根据三角形的中线的定义得到AF=FC,再根据三角形的周长公式计算,得到答案.
解:(1)∵AD是△ABC的高,
∴∠ADB=90°,
∵∠BAD=70°,
∴∠ABC=90°﹣70°=20°,
∵CE是△ACB的角平分线,∠ACB=50°,
∴∠ECB=∠ACB=×50°=25°,
∴∠AEC=∠ABC+∠ECB=20°+25°=45°;
(2)能求出BC的值,
理由如下:∵F是AC中点,
∴AF=FC,
∵△BCF与△BAF的周长差为3,
∴(BC+CF+BF)﹣(AB+AF+BF)=3,
∴BC﹣AB=3,
∵AB=7,
∴BC=3+7=10.
【点评】本题考查的是三角形的高、中线、角平分线,掌握它们的概念是解题的关键.
23.如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连接CD、DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,EC=8时,求△EDC的面积.
【分析】(1)根据等边三角形的性质,即可证明结论;
(2)设∠EDB=α,则∠BDC=5α,得∠E=∠DCE=60°﹣α,根据三角形内角和定理可得α=15°,过D作DH⊥CE于H,根据等腰直角三角形的性质即可得DH的长,进而可得结论.
【解答】(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵∠E+∠EDB=∠ABC=60°,∠ACD+∠DCB=60°,∠EDB=∠ACD,
∴∠E=∠DCE,
∴DE=DC,
∴△DEC是等腰三角形;
(2)解:设∠EDB=α,则∠BDC=5α,
∴∠E=∠DCE=60°﹣α,
∴6α+60°﹣α+60°﹣α=180°,
∴α=15°,
∴∠E=∠DCE=45°,
∴∠EDC=90°,
如图,过D作DH⊥CE于H,
∵△DEC是等腰直角三角形,
∴∠EDH=∠E=45°,
∴EH=HC=DH=EC=8=4,
∴△EDC的面积=EC•DH=8×4=16.
【点评】本题考查了等边三角形的性质,等腰三角形的判定与性质,解决本题的关键是掌握等边三角形的性质,等腰三角形的判定与性质.
24.问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF ;
探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
【分析】问题背景:延长FD到点G,使DG=BE,连接AG,证明△ABE≌△ADG,得到△AEF≌△AGF,证明EF=FG,得到答案;
探索延伸:连接EF,延长AE,BF相交于点C,利用全等三角形的性质证明EF=AE+FB.
实际应用:如图3,连接EF,延长AE,BF相交于点C,首先证明,∠FOE=∠AOB,利用结论EF=AE+BF求解即可.
解:问题背景:由题意:△ABE≌△ADG,△AEF≌△AGF,
∴BE=DG,EF=GF,
∴EF=FG=DF+DG=BE+FD.
故答案为:EF=BE+FD.
探索延伸:EF=BE+FD仍然成立.
理由:如图2,延长FD到点G,使DG=BE,连接AG
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG,
又∵AB=AD,
在△ABE和△ADG中,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
又∵∠EAF=∠BAD,
∴∠FAG=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD﹣∠EAF,
=∠BAD﹣∠BAD=∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
又∵FG=DG+DF=BE+DF,
∴EF=BE+FD.
实际应用:如图3,连接EF,延长AE,BF相交于点C,
在四边形AOBC中,
∵∠AOB=30°+90°+20°=140°,∠FOE=70°=∠AOB,
又∵OA=OB,∠OAC+∠OBC=60°+120°=180°,符合探索延伸中的条件,
∴结论EF=AE+FB成立.
即,EF=AE+FB=2×(70+90)=320(海里)
答:此时两舰艇之间的距离为320海里.
【点评】本题考查的是四边形知识的综合运用,掌握三角形全等的判定和性质、理解方位角的概念是解题的关键,注意规律的总结和运用.
相关试卷
这是一份浙江省温州市苍南县六校联考2023-2024学年八年级上学期期中数学试卷,共4页。
这是一份浙江省温州市苍南县灵溪镇2023--2024学年九年级上学期六校联考期中检测数学试卷,共4页。
这是一份2022-2023学年浙江省温州市苍南县七校联盟八年级(下)第二次月考数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。