华师大版九年级上册24.4 解直角三角形课文配套ppt课件

这是一份华师大版九年级上册24.4 解直角三角形课文配套ppt课件，共19页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，坡角问题等内容，欢迎下载使用。
坡角问题 利用解直角三角形解决实际问题的一般步骤
读一读 在修路、挖河、开渠和筑坝时，设计图纸上都要注明斜坡的倾斜程度. 如图24. 4. 5,坡面的铅垂高度（ h）和水平长度（ l）的比叫做坡面的坡度（或坡比），记作i,即i = . 坡度通常写成1 :m的形式，如 i =1 :6. 坡面与水平面的夹角叫做坡角，记作α， 有 显然，坡度越大，坡角α就越大，坡面就越陡.
坡角、坡度问题在实际生活中，正切经常用来描述坡面的倾斜程度， 坡面与水平面的夹角叫做坡角(或称倾斜角)，人们经 常把坡面的铅垂高度h和水平长度l的比叫做坡面的坡 度(或坡比)，如图24.4­8所示，记作：i＝ ；坡度越大，坡角α就越大，坡面就越陡，即tan α的值 就越大．
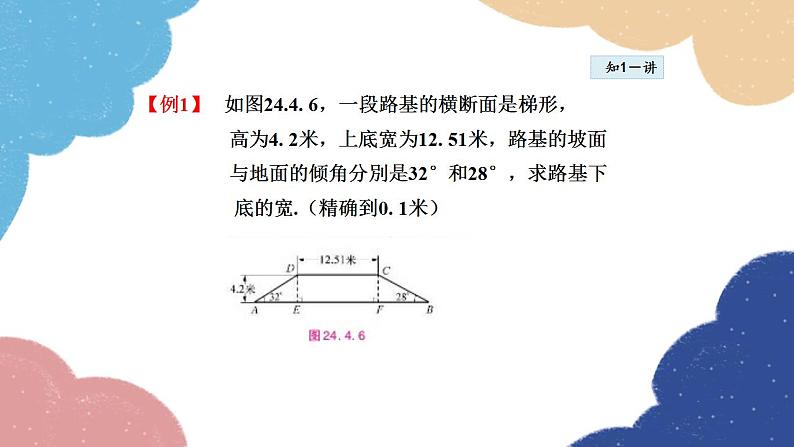
【例1】 如图24.4. 6，一段路基的横断面是梯形， 高为4. 2米，上底宽为12. 51米，路基的坡面 与地面的倾角分別是32°和28°，求路基下 底的宽.（精确到0. 1米）
解： 作DE⊥AB，CF⊥AB，垂足分别为点E、F 由题意 可知 DE = CF = 4.2, EF = CD = 12.51. 在 Rt△ADE 中，  在Rt△ BCF中，同理可得 ∴AB = AE + EF + BF ≈6. 72 + 12.51 +7.90≈27. 1(米). 答：路基下底的宽约为27. 1米.
【例2】 〈广东〉如图所示，小山岗的斜坡AC的坡度 tan α＝ ，在与山脚C距离200 m的D处，测 得山顶A的仰角为26.6°，求小山岗的高AB. (结果取整数，参考数据：sin 26.6°≈ 0.45， cs 26.6°≈ 0.89，tan 26.6°≈ 0.50)
导引： 设小山岗的高AB为x m，∵在Rt△ABC中，在Rt△ABD中，tan 26.6°＝ 而BD＝BC＋DC，∴可得关于x的方程，解之即可求得AB的长．
解： 设小山岗的高AB为x m，在Rt△ABC中，  ∴BC＝ x m． ∴BD＝DC＋BC＝ ∵在Rt△ABD中，tan∠ADB＝ tan 26.6°≈0.50， ∴ ≈0.50，解得x≈300.答：小山岗的高AB约为300 m.
如图，某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B，如果AB＝2 000米，则他实际上升了________米．
拦水坝横断面如图所示，迎水坡AB的坡比是1∶ ，坝高BC＝10 m，则坡面AB的长 度是(　　) A．15 m　　B．20 m　C．10 m　D．20 m
利用解直角三角形解决实际问题的一般步骤
1. 利用解直角三角形的知识解决实际问题的一般过程是：（1）将实际问题抽象为数学问题（画出平面图形，转化 为解直角三角形的问题，也就是建立适当的数学模 型）；（2）根据条件的特点，适当选用锐角三角函数，运用直 角三角形的有关性质，解直角三角形；（3）得到数学问题的答案；（4）得到实际问题的答案.
2. 易错警示： ① 在解决方向角问题时，要将方向角正确地转化为 直角三角形的内角使用．在利用仰角、俯角解决问题时，一定要注意测角 仪的高度是否在所测物的高度中．③ 在解决坡度问题时，要正确理解坡度与锐角三角 函数的联系，正确列出相应的关系式．
【例3】 〈山东青岛，实际应用题〉如图所示，某校教学楼 AB的后面有一建筑物CD，当光线与地面的夹角是 22°时，教学楼在建筑物的墙上留下高2 m的影子 CE；而当光线与地面的夹角是45°时，教学楼楼 顶A在地面上的影子F与墙脚C有13 m的距离(B、F、 C在一条直线上)． (1) 求教学楼AB的高度； (2) 学校要在点A、E之间挂一些 彩旗，请你求出点 A、E之间 的距离(结果保留整数)． (参考数据：sin 22°≈ ， cs 22°≈ ，tan 22°≈ )
导引： 如图，过E作EM⊥AB于M， (1)设AB＝x m，由 tan 22°＝ 求x的值即可． (2)由cs 22°＝ 得
解： (1) 如图，过点E作EM⊥AB，垂足为M，设AB＝x m. 在Rt△ABF中，∠AFB＝45°，∴BF＝AB＝x m. ∴BC＝BF＋FC＝(x＋13) m. 在Rt△AEM中，∠AEM＝22°，AM＝AB－BM＝ AB－CE＝(x－2) m， ∴tan 22°= 解得x≈12. 即教学楼AB的高度为12 m.
(2) 由(1)可得ME＝BC＝x＋13 ≈ 12＋13＝25(m)．在Rt△AME中，cs 22°＝ ∴即点A、E之间的距离约为27 m.
本题是解直角三角形与方程的综合，在有关直角三角形的应用题中，当利用勾股定理或锐角三角函数不能直接解直角三角形时，常引入未知数构造方程求解，体现了方程思想及数形结合思想．
1. 如图，某仓储中心有一斜坡AB，其坡度为i＝1∶2，顶部A处的高AC为4 m，B，C在同一水平地面上． (1) 求斜坡AB的水平宽度BC； (2) 矩形DEFG为长方体货柜的侧面图，其中DE＝2.5 m， EF＝2 m，将该货柜沿斜坡向上运送，当BF＝3.5 m 时，求点D离地面的高度．( ≈2.236，结果精确到 0.1 m)