初中数学人教版七年级上册2.2 整式的加减精品备课教学ppt课件

这是一份初中数学人教版七年级上册2.2 整式的加减精品备课教学ppt课件，共33页。PPT课件主要包含了a+3ab，×-2，100+252t，－252，ab2－4ab2，-152t，x2＋2x2，3＋2x2，5x2，-ab2等内容，欢迎下载使用。
1.知道同类项的概念，会识别同类项.2.掌握合并同类项的法则，并能准确合并同类项.3.能在合并同类项的基础上进行化简、求值运算.
1.银行职员数钞票时，把100元票面、50元票面、20元票面、10元票面…的人民币分类来数，在多项式中是否也有类似的情形呢？
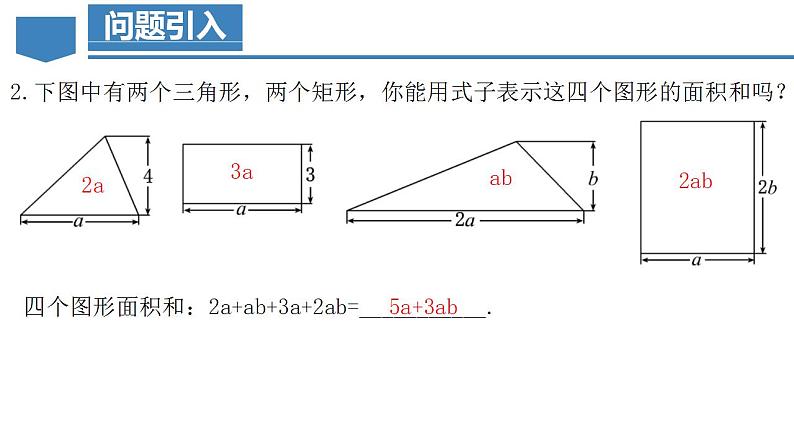
2.下图中有两个三角形，两个矩形，你能用式子表示这四个图形的面积和吗？
四个图形面积和：2a+ab+3a+2ab=___________.
(1) 运用运算律计算： 100×2＋252×2=______________； 100×(-2)＋252×(-2)=________________；(2) 根据(1)中的方法完成下面的运算，并说明其中的道理： 100t＋252t=____________.
(100+252)×2
(100+252)×(-2)
在(1)中，我们知道，根据分配律可得 100×2＋252×2
=(100＋252)×2
100×(-2)＋252×(-2)
=(100＋252)×(-2)
在(2)中，式子100t＋252t表示100t与252t两项的和.它与(1)中的两个式子有相同的结构，并且字母t代表的是一个因(乘)数，因此根据分配律也应该有
=(100＋252)t
100t－252t=( )t；3x2＋2x2=( )x2；3ab2－4ab2=( )ab2.上述运算有什么共同特点，你能从中得出什么规律吗？
对于上面的(1)(2)(3)，利用分配律可得100t－252t
=(100－252)t
多项式100t－252t的项100t和-252t，多项式3x2＋2x2的项3x2和2x2，多项式3ab2－4ab2的项3ab2和-4ab2，
它们含有相同的字母t，并且t的指数
它们含有相同的字母a、b，并且a的指
它们含有相同的字母x，并且x的指数都是2；
数都是1次，b的指数都是2次.
同类项： 像100t与-252t，3x2与2x2，3ab2与-4ab2这样，所含字母相同，并且相同字母的指数也相同的项叫做同类项. 几个常数项也是同类项. 例如5与-3.
（1）同类项只与字母及其指数有关，与系数无关，与字母在单项式中的排列顺序无关；（2）抓住“两个相同”：一是所含的字母要完全相同，二是相同字母的指数要相同，这两个条件缺一不可.
（3）不要忘记几个单独的数也是同类项.
因为多项式中的字母表示的是数，所以我们也可以运用交换律、结合律、分配律把多项式中的同类项进行合并.例如，
4x2＋2x＋7＋3x－8x2－2
=4x2－8x2＋2x＋3x＋7－2
=(4x2－8x2)＋(2x＋3x)＋(7－2)
=(4－8)x2＋(2＋3)x＋(7－2)
通常我们把一个多项式的各项按照某个字母的指数从大到小(降幂)或者从小到大(升幂)的顺序排列，如－4x2＋5x＋5也可以写成5＋5x－4x2.
【分析】把一个多项式按照某一字母的指数从大到小的顺序排列起来，叫做把多项式按照这个字母降幂排列．
多项式的升(降)幂排列
2.合并同类项的法则：
同类项的系数相加，所得的结果作为系数，字母和字母的指数不变.
1.把多项式中的同类项合并成一项叫做合并同类项.
解:(1)4a2-9b-3a2+8b. =(4a2-3a2)+(-9b+8b) =(4-3)a2+(-9+8)b=a2-b;
例3.合并同类项:(1)4a2-9b-3a2+8b； (2)x3-3x2-2+4x2-1； (3)-4a2b-3ab+1+3ab-2a2b-4.
不同组的同类项用“+”号相连
(2)x3-3x2-2+4x2-1=x3+(-3x2+4x2)+(-2-1) =x3+(-3+4)x2+(-2-1) =x3+x2-3;
没有同类项的单项式在每一步都要写出,不能漏掉!
(3)-4a2b-3ab+1+3ab-2a2b-4=(-4a2b-2a2b)+(-3ab+3ab)+(1-4)=(-4-2)a2b+(-3+3)ab+(1-4)=-6a2b-3.
系数互为相反数的同类项合并后为0
“合并同类项”的方法： 一找，找出多项式中的同类项，不同类的同类项用不同的标记标出； 二移，利用加法的交换律，将不同类的同类项集中到不同的括号内； 三合，将同一括号内的同类项相加即可.
1.-4a2b+3ab=(-4+3)a2b=-a2b,上述运算依据的运算律是( )A.加法交换律 B.乘法交换律 C.分配律 D.乘法结合律2.下列计算正确的是( )A.3x2-x2=3 B.a+b=ab C.3+x=3x D.-ab+ab=03.合并同类项:(1)-2x2y-3x2y+5x2y; (2)3x2+2xy-5x-3y2-6xy.
解:(1)原式=(-2-3+5)x2y=0;(2)原式=(3-5)x2+(2-6)xy-3y2=-2x2-4xy-3y2.
例4.求多项式3x2+4x-2x2-x+x2-3x-1的值，其中x=-3.
解:原式=(3x2-2x2+x2)+(4x-x-3x)-1=(3-2+1)x2+(4-1-3)x-1=2x2-1当x=-3时，原式=2×(-3)2-1=17.
1.当x=2025时，3x2+x-4x2-2x+x2+2024的值为______.2.求多项式a2b-6ab-3a2b+5ab+2a2b的值，其中a=0.1，b=0.01.
解:原式=(a2b-3a2b+2a2b)+(-6ab+5ab)=(1-3+2)a2b+(-6+5)ab=-ab当a=0.1，b=0.01时，原式=-0.1×0.01=-0.001.
例5.七年级有三个班参加了植树活动，其中一班植树x棵，二班植树棵数比一班的2倍少5，三班植树棵数比一班的一半多10.这三个班一共植树多少棵?
最后的结果要是最简形式(不含同类项)
张老师家住房结构如图所示(图中长度单位:m)，他打算在卧室和客厅铺上木地板.请你帮他算一算，他至少需要木地板_____m2.
解:因为-4xaya+1与mx5yb-1的和是3x5yn，所以-4+m=3，a=5，a+1=b-1=n.所以a=5，b=7，m=7，n=6.所以(m-n)(2a-b)=(7-6)×(2×5-7)=3.
多项式中“无关”“不含”“多余”的问题
例7.已知关于x，y的多项式2x2+ax-y+6-2bx2+3x-5y-2的值与字母x的取值无关，求a，b的值.
解:2x2+ax-y+6-2bx2+3x-5y-2=(2-2b)x2+(a+3)x+(-1-5)y+(6-2)=(2-2b)x2+(a+3)x-6y+4因为多项式的值与x的取值无关所以2-2b=0，a+3=0，所以a=-3，b=1.
1.若关于x的多项式-3x2+mx+nx2-x+3的值与x的取值无关，则m，n的值分别为( )A.-1，-3 B.1，3 C.-1，3 D.1，-32.若关于x，y的多项式mx3+3nxy2-2x3-xy2+y中不含三次项，则2m+3n的值为______.
解:有道理.理由如下:原式=(7+3-10)x3+(-6+6)x3y+(3-3)x2y+3=3.该多项式的值与x,y的取值无关.所以小聪同学的说法有道理.
（2）相同字母的指数相同.
（2）字母连同它的指数不变.