初中人教版3.1.1 一元一次方程优秀备课教学ppt课件

这是一份初中人教版3.1.1 一元一次方程优秀备课教学ppt课件，共21页。PPT课件主要包含了x-2000，去括号，x162000，x13500，合并同类项，系数化为1，x+2000等内容，欢迎下载使用。

1. 了解“去括号”是解方程的重要步骤.2. 准确而熟练地运用去括号法则解带有括号的一元一次方程.
如果括号外的因数是正数，___________________________________________________________；如果括号外的因数是负数，___________________________________________________________.
化简：(1) -2(3x+2)+4(x-2) (2) -3(3y-1)-(y+10)
解：(1)原式=-6x-4+4x-8=-2x-12；(2)原式=-9y+3-y-10=-10y-7.
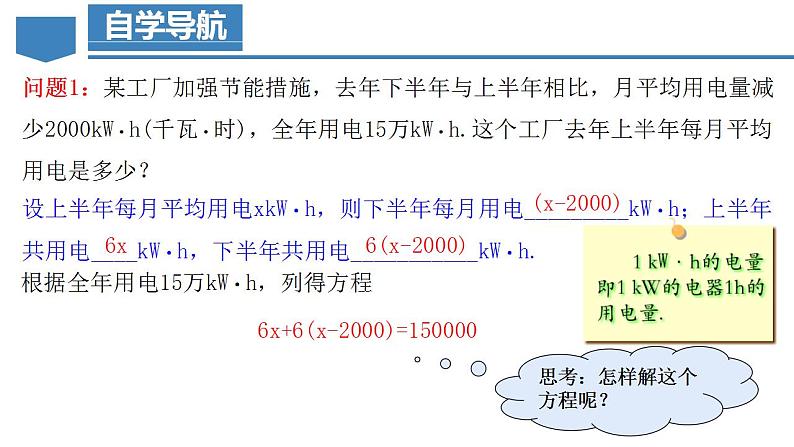
问题1：某工厂加强节能措施，去年下半年与上半年相比，月平均用电量减少2000kW·h(千瓦·时)，全年用电15万kW·h.这个工厂去年上半年每月平均用电是多少？
设上半年每月平均用电xkW·h，则下半年每月用电_________kW·h；上半年共用电____kW·h，下半年共用电___________kW·h.
根据全年用电15万kW·h，列得方程
6x+6(x-2000)=150000
思考：怎样解这个方程呢？
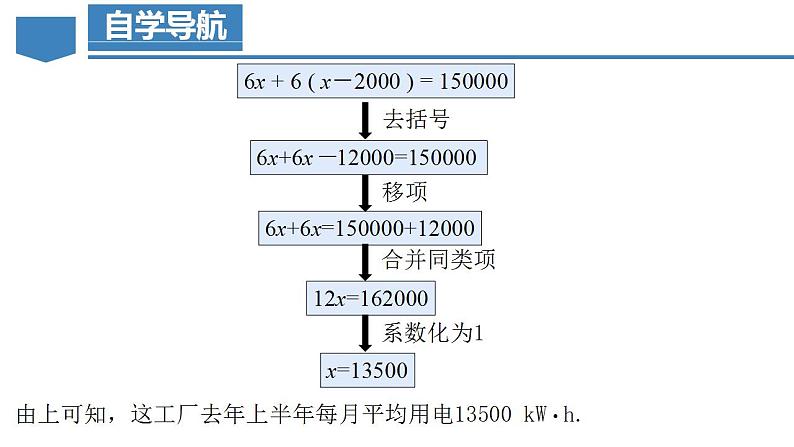
6x + 6 ( x－2000 ) = 150000
6x+6x－12000=150000
6x+6x=150000+12000
由上可知，这工厂去年上半年每月平均用电13500 kW·h.
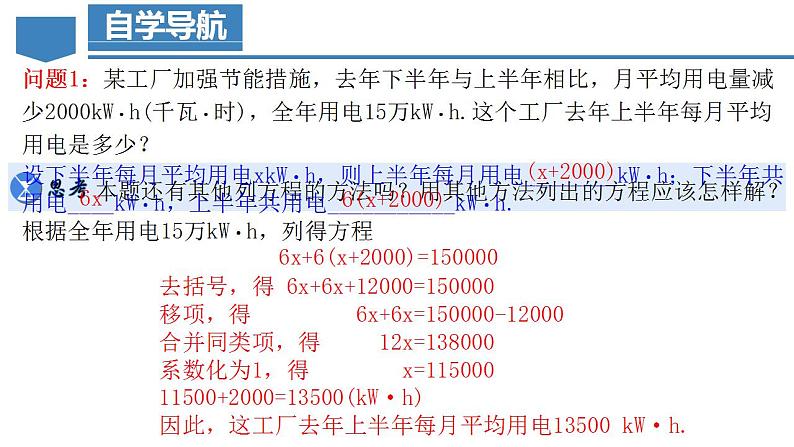
设下半年每月平均用电xkW·h，则上半年每月用电________kW·h；下半年共用电____kW·h，上半年共用电___________kW·h. 根据全年用电15万kW·h，列得方程
6x+6(x+2000)=150000
去括号，得 6x+6x+12000=150000移项，得 6x+6x=150000-12000合并同类项，得 12x=138000系数化为1，得 x=11500011500+2000=13500(kW·h)因此，这工厂去年上半年每月平均用电13500 kW·h.
利用去括号解一元一次方程
例1.解下列方程:(1)x-(5x-3)=-3x+2(2x-1)； (2)4x-5(x-3)=12-3(x+3).
分析:按“去括号、移项、合并同类项、系数化为1”的步骤解方程.
解:(1)去括号，得x-5x+3=-3x+4x-2.移项，得x-5x+3x-4x=-2-3.合并同类项，得-5x=-5.系数化为1，得x=1.
(2)去括号，得4x-5x+15=12-3x-9.移项，得4x-5x+3x=12-9-15.合并同类项，得2x=-12.系数化为1，得x=-6.
1.解方程-2(2x+1)=x，以下去括号正确的是( )A.-4x+1=-x B.-4x+2=-x C.-4x-1=x D.-4x-2=x2.方程2(x-3)=6的解是_______.3.若3a+1与3(a+1)互为相反数，则a=_______.
解:(1)去括号，得4-x=x-2+x.移项，得-x-x-x=-2-4.合并同类项，得-3x=-6.系数化为1，得x=2.
(2)去括号，得2-y=-2y-2.移项，得-y+2y=-2-2.合并同类项，得y=-4.
(3)去括号，得3x-9=10x-14+6-6x.移项，得3x-10x+6x=-14+6+9.合并同类项，得-x=1.系数化为1，得x=-1.
利用去括号解一元一次方程解决顺流( 风)、逆流(风)问题
例2.一艘船从甲码头顺流航行到乙码头用时4h，从乙码头返回甲码头用时5h.已知水流的速度为3km/h，求甲、乙两个码头之间的航程.
分析:①设船在静水中的平均速度为xkm/h.列表表示数量关系:②相等关系:顺流航程=逆流航程.
解:设船在静水中的平均速度为xkm/h.根据题意,得4(x+3)=5(x-3)，解得x=27.所以4(x+3)=120.答:甲、乙两个码头之间的航程为120km.
1.一艘轮船从甲地顺水开往乙地，所用时间比从乙地逆水开往甲地少1.5h.已知船在静水中的速度为18km/h，水流速度为2km/h，则甲、乙两地之间的航程为_______km.
【解析】设船从乙地逆水航行开往甲地需xh.根据题意，得(18+2)(x-1.5)=(18-2)x，解得x=7.5.所以(18-2)×7.5=120.故甲、乙两地之间的航程为120km.
2.一架飞机在两个城市之间飞行，当顺风飞行时需2.9h，当逆风飞行时则需3.2h.已知风速为30km/h，求无风时飞机的航速和这两个城市之间的航程.
解:设无风时飞机的航速为xkm/h.由题意，得(x+30)×2.9=(x-30)×3.2.解得x=610.所以(x+30)×2.9=(610+30)×2.9=1856(km).答:无风时飞机的航速为610km/h，这两个城市之间的航程为1856km.
利用方程同解求字母的值
例3.若方程3(2x-2)=2-3x的解与关于x的方程6-2k=2(x+3)的解相同，则k的值为______.
利用去括号解决实际问题
例4.甲地到乙地的高铁开通后，运行时间由原来的3.5h缩短至1h，运行里程缩短了40km.已知高铁的平均速度比普通列车的平均速度每小时快200km，求高铁的平均速度.
分析:①列表表示数量关系:②相等关系:高铁里程+40=普通列车里程.
解:设高铁的平均速度为xkm/h,则普通列车的平均速度为(x-200)km/h.由题意得,x+40=3.5(x-200).解得x=296. 答:高铁的平均速度为296km/h.
一快递员需要在规定时间内开车将快递送到某地，若快递员开车每分钟行驶1.2km，就早到10分钟；若快递员开车每分钟行驶0.8km，就要迟到5分钟.试求出规定时间.
解:设规定时间为:x min.根据题意得，1.2(x-10)=0.8(x+5)，解得x=40.答:规定时间为40min.