辽宁省大连市高新区2023-2024学年八年级上学期期中数学试卷

这是一份辽宁省大连市高新区2023-2024学年八年级上学期期中数学试卷，共32页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（2分）剪纸文化是中国最古老的民间艺术之一，下列剪纸图案中，不是轴对称图形的是（ ）
A．B．
C．D．
2．（2分）正八边形的外角和为（ ）
A．540°B．360°C．720°D．1080°
3．（2分）在下列长度的四根木棒中，能与5cm、9cm长的两根木棒钉成一个三角形的是（ ）
A．3cmB．4cmC．5cmD．14cm
4．（2分）在平面直角坐标系中，点P（﹣2，3）关于x轴对称的点的坐标是（ ）
A．（2，3）B．（﹣2，3）C．（2，﹣3）D．（﹣2，﹣3）
5．（2分）根据下列已知条件，不能画出唯一△ABC的是（ ）
A．∠A＝60°，∠B＝45°，AB＝4B．∠A＝30°，AB＝5，BC＝3
C．∠B＝60°，AB＝6，BC＝10D．∠C＝90°，AB＝5，BC＝3
6．（2分）若等腰三角形的两边长分别为2和5，则它的周长为（ ）
A．9B．7C．12D．9或12
7．（2分）如图，已知△ABC≌△BDE，∠ABC＝∠ACB＝70°，则∠ABE的度数为（ ）
A．25°B．30°C．35°D．40°
8．（2分）如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝36cm2，AB＝18cm，BC＝12cm，则DE的长为（ ）
A．2cmB．cmC．cmD．3cm
9．（2分）如图，在△ABC中，∠ACB＝90°，AC＜BC．分别以点A，B为圆心；大于的长为半径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF．以点A为圆心，AF为半径画弧，交BC延长线于点H，连接AH．若BC＝3，则△AFH的周长为（ ）
A．3B．4C．5D．6
10．（2分）如图，△ABC≌△DEF，FH⊥BC，垂足为E．若∠A＝α，∠CHE＝β，则∠BED的大小为（ ）
A．α﹣βB．90°+α﹣βC．β﹣αD．90°﹣α+β
二、填空题（本题共6小题，每小题3分，共18分）
11．（3分）如图，△ABC中，∠B＝35°，∠ACD＝120°，则∠A＝ ．
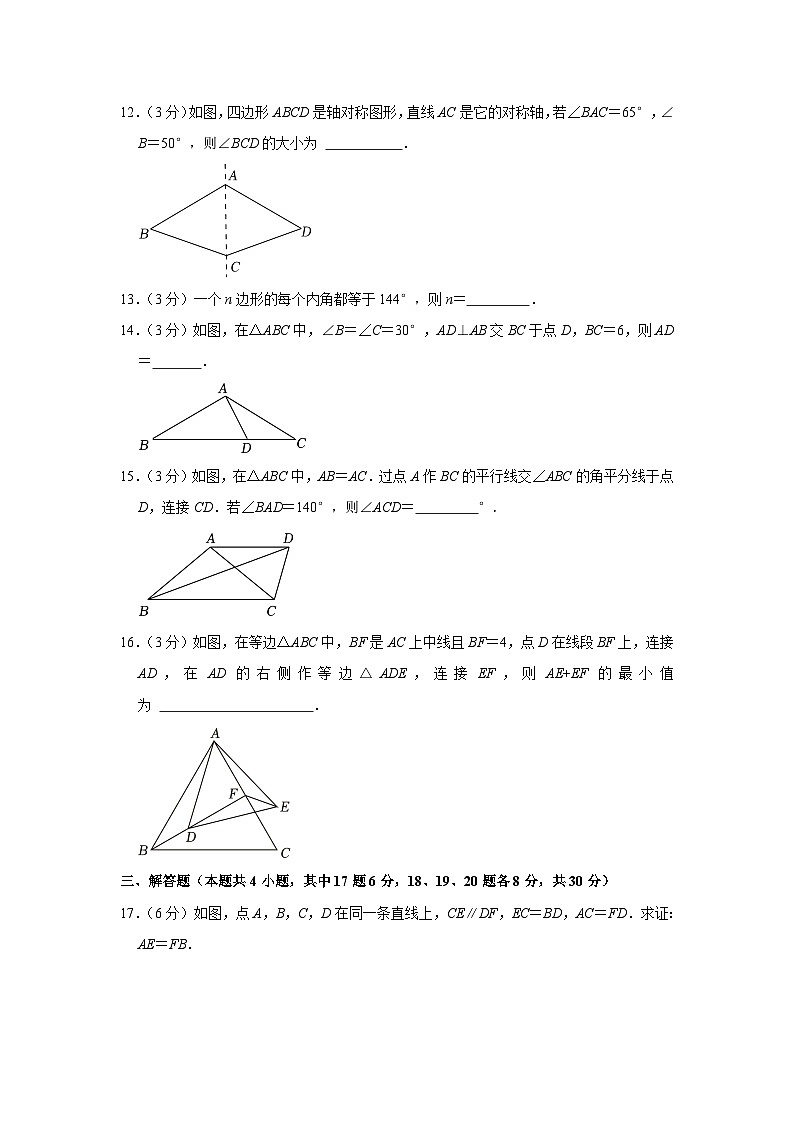
12．（3分）如图，四边形ABCD是轴对称图形，直线AC是它的对称轴，若∠BAC＝65°，∠B＝50°，则∠BCD的大小为 ．
13．（3分）一个n边形的每个内角都等于144°，则n＝ ．
14．（3分）如图，在△ABC中，∠B＝∠C＝30°，AD⊥AB交BC于点D，BC＝6，则AD＝ ．
15．（3分）如图，在△ABC中，AB＝AC．过点A作BC的平行线交∠ABC的角平分线于点D，连接CD．若∠BAD＝140°，则∠ACD＝ °．
16．（3分）如图，在等边△ABC中，BF是AC上中线且BF＝4，点D在线段BF上，连接AD，在AD的右侧作等边△ADE，连接EF，则AE+EF的最小值为 ．
三、解答题（本题共4小题，其中17题6分，18、19、20题各8分，共30分）
17．（6分）如图，点A，B，C，D在同一条直线上，CE∥DF，EC＝BD，AC＝FD．求证：AE＝FB．
18．（8分）如图，在△ABC中，AB＝AC，D为BC边上一点，AD＝BD，AC＝DC．求∠BAC的度数．
19．（8分）如图为某单摆装置示意图，摆线长OA＝OB＝OC，当摆线位于OB位置时，过点B作BD⊥OA于点D，测得OD＝15cm，当摆线位于OC位置时，OB与OC恰好垂直，求此时摆球到OA的水平距离CE的长（CE⊥OA）．
20．（8分）如答题卡中的图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．
（1）请以x轴为对称轴，画出与△ABC对称的△A1B1C1，并直接写出点A1、B1、C1的坐标；
（2）点P（a+1，b﹣2）与点C关于y轴对称，则a＝ ，b＝ ．
四、解答题（本题共2小题，其中21题8分，22题10分，共18分）
21．（8分）如图，在△ABC中，∠BAC的平分线与BC的中垂线DE交于点E，过点E作AC边的垂线，垂足N，过点E作AB延长线的垂线，垂足为M．
（1）求证：BM＝CN；
（2）若AB＝2，AC＝8，求BM的长．
22．（10分）已知：如图，AC∥BD，请先作图再解决问题．
（1）利用尺规完成以下作图，并保留作图痕迹，（不要求写作法）
①作BE平分∠ABD交AC于点E；
②在BA的延长线上截取AF＝BA，连接EF；
（2）判断△BEF的形状，并说明理由．
五、解答题（本题共2小题，其中23题10分，24题12分，共22分）
23．（10分）如图，长方形ABCD中，AB＝4cm，BC＝6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A﹣B﹣C﹣D﹣A返回到点A停止，设点P运动的时间为t秒．
（1）当t＝3时，BP＝ cm；
（2）当t为何值时，连接CP，DP，△CDP是等腰三角形；
（3）Q为AD边上的点，且DQ＝5，当t为何值时，以长方形的两个顶点及点P为顶点的三角形与△DCQ全等．
24．（12分）在△ABC中，AB＝AC，∠BAC＝α，射线AD，AE的夹角为，过点B作BF⊥AD于点F，直线BF交AE于点G，连结CG．
（1）如图1，射线AD，AE都在∠BAC内部．
①若α＝120°，∠CAE＝20°，则∠CBG＝ °；
②作点B关于直线AD的对称点H，在图1中找出与线段GH相等的线段，并证明．
（2）如图2，射线AD在∠BAC的内部，射线AE在∠BAC的外部，其它条件不变，探究线段BF，BG，CG之间的数量关系，并证明．
六、解答题（本题12分）
25．（12分）综合与实践
阅读材料：
材料1：如图1，在Rt△ABC中，∠ACB＝90°，∠A＝60°，以C为圆心，CA长为半径画弧，交AB边于点D，连结CD，则△ACD是等边三角形，△BCD是等腰三角形．
材料2：如图2，△ABC是等边三角形，D为直线BD上一点，以AD为边在AD右侧作等边△ADE，连结CE，随着D点位置的改变，始终有△ABD≌△ACE．
根据上述阅读材料，解决下面的问题．
已知，在△ABC中，∠ACB＝90°，∠A＝60°，D为AB边上一点，以CD为边在CD右侧作等边△CDE．
特例探究：（1）如图3，当点E在AB边上时，求证：DE＝BE．
感悟应用：（2）如图4，当点E在△ABC内部时，连结BE，求证：DE＝BE．
拓展延伸：（3）当点E在△ABC的外部时，过点E作EH⊥AB于H，EF∥AB交射线AC于F，CF＝2，BH＝3，请画出图形，并求AB的长．
参考答案与试题解析
一、选择题（本题共10小题，每小题2分，共20分，在每小题给出的四个选项中，只有一个选项正确）
1．（2分）剪纸文化是中国最古老的民间艺术之一，下列剪纸图案中，不是轴对称图形的是（ ）
A．B．
C．D．
【分析】根据轴对称图形的概念逐项分析判断即可，轴对称图形的概念：平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．
【解答】解：选项A、B、D均能找到这样的一条直线，使直线两旁的部分能够完全重合的图形，所以是轴对称图形；
选项C，不能找到这样的一条直线，使直线两旁的部分能够完全重合的图形，所以不是轴对称图形；
故选：C．
【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．（2分）正八边形的外角和为（ ）
A．540°B．360°C．720°D．1080°
【分析】根据多边形的外角和等于360°解答即可．
【解答】解：∵任意多边形的外角和等于360°，
∴正八边形的外角和等于360°，
故选：B．
【点评】本题考查了多边形的外角，掌握多边形的外角和等于360°是解题的关键．
3．（2分）在下列长度的四根木棒中，能与5cm、9cm长的两根木棒钉成一个三角形的是（ ）
A．3cmB．4cmC．5cmD．14cm
【分析】根据三角形的三边关系确定第三边的范围，判断即可．
【解答】解：设第三边的长为xcm，
则9﹣5＜x＜9+5，即4＜x＜14，
∴四根木棒中，长度为5cm的木棒，能与5cm、9cm长的两根木棒钉成一个三角形，
故选：C．
【点评】本题考查的是三角形的三边关系，熟记三角形两边之和大于第三边、三角形的两边差小于第三边是解题的关键．
4．（2分）在平面直角坐标系中，点P（﹣2，3）关于x轴对称的点的坐标是（ ）
A．（2，3）B．（﹣2，3）C．（2，﹣3）D．（﹣2，﹣3）
【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答即可．
【解答】解：点P（﹣2，3）关于x轴对称的点的坐标为（﹣2，﹣3）．
故选：D．
【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：
（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；
（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数．
5．（2分）根据下列已知条件，不能画出唯一△ABC的是（ ）
A．∠A＝60°，∠B＝45°，AB＝4B．∠A＝30°，AB＝5，BC＝3
C．∠B＝60°，AB＝6，BC＝10D．∠C＝90°，AB＝5，BC＝3
【分析】根据全等三角形的判定定理逐个判断即可．
【解答】解：A．∠A＝60°，∠B＝45°，AB＝4，符合全等三角形的判定定理ASA，能画出唯一的△ABC，故本选项不符合题意；
B．∠A＝30°，AB＝5，BC＝3，不符合全等三角形的判定定理，不能画出唯一的△ABC，故本选项符合题意；
C．∠B＝60°，AB＝6，BC＝10，符合全等三角形的判定定理SAS，能画出唯一的△ABC，故本选项不符合题意；
D．∠C＝90°，AB＝5，BC＝3，符合全等直角三角形的判定定理HL，能画出唯一的△ABC，故本选项不符合题意；
故选：B．
【点评】本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有HL．
6．（2分）若等腰三角形的两边长分别为2和5，则它的周长为（ ）
A．9B．7C．12D．9或12
【分析】求等腰三角形的周长，即是确定等腰三角形的腰与底的长求周长；题目给出等腰三角形有两条边长为2和5，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
【解答】解：（1）若2为腰长，5为底边长，
由于2+2＜5，则三角形不存在；
（2）若5为腰长，则符合三角形的两边之和大于第三边．
所以这个三角形的周长为5+5+2＝12．
故选：C．
【点评】本题考查了等腰三角形的性质和三角形的三边关系；题目从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．
7．（2分）如图，已知△ABC≌△BDE，∠ABC＝∠ACB＝70°，则∠ABE的度数为（ ）
A．25°B．30°C．35°D．40°
【分析】先根据三角形内角和计算出∠A＝40°，再根据全等三角形的性质得到∠DBE＝∠A＝40°，然后计算∠ABC﹣∠DBE即可．
【解答】解：∵∠ABC＝∠ACB＝70
∴∠A＝180°﹣70°﹣70°＝40°，
∵△ABC≌△BDE，
∴∠DBE＝∠A＝40°，
∴∠ABE＝∠ABC﹣∠DBE＝70°﹣40°＝30°．
故选：B．
【点评】本题考查了全等三角形的性质：全等三角形的对应角相等．
8．（2分）如图，BD是∠ABC的平分线，DE⊥AB于E，S△ABC＝36cm2，AB＝18cm，BC＝12cm，则DE的长为（ ）
A．2cmB．cmC．cmD．3cm
【分析】过点D作DF⊥BC于F，根据角平分线上的点到角的两边距离相等可得DE＝DF，然后根据△ABC的面积列出方程求解即可得到DE．
【解答】解：如图，过点D作DF⊥BC于F，
∵BD是∠ABC的平分线，DE⊥AB，
∴DE＝DF，
∵S△ABC＝36cm2，AB＝18cm，BC＝12cm，
∴S△ABC＝S△ABD+S△BCD＝AB•DE+BC•DF＝DE•（AB+BC）＝36cm2，
解得：DE＝（cm）．
故选：C．
【点评】此题考查了角平分线的性质，三角形的面积公式，正确作出辅助线是解题的关键．
9．（2分）如图，在△ABC中，∠ACB＝90°，AC＜BC．分别以点A，B为圆心；大于的长为半径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF．以点A为圆心，AF为半径画弧，交BC延长线于点H，连接AH．若BC＝3，则△AFH的周长为（ ）
A．3B．4C．5D．6
【分析】直接利用基本作图方法得出DE垂直平分AB，AF＝AH，再利用等腰三角形的性质、线段垂直平分线的性质得出AF+FC＝BF+FC＝BC，即可得出答案．
【解答】解：由基本作图方法得出：DE垂直平分AB，
则AF＝BF，
∴AF+FC＝BF+FC＝BC＝3，
而AF＝AH，AC⊥FH，
∴FC＝CH，
∴AF+FC＝AH+HC＝BC＝3，
∴△AFH的周长为：AF+FC+CH+AH＝2BC＝6．
故选：D．
【点评】此题主要考查了基本作图以及等腰三角形的性质、线段垂直平分线的性质等知识，正确得出AF+FC＝BF+FC＝BC是解题关键．
10．（2分）如图，△ABC≌△DEF，FH⊥BC，垂足为E．若∠A＝α，∠CHE＝β，则∠BED的大小为（ ）
A．α﹣βB．90°+α﹣βC．β﹣αD．90°﹣α+β
【分析】根据直角三角形两锐角互余求出∠C＝90°﹣∠CHE＝90°﹣β，由三角形内角和定理得出∠B＝180°﹣∠A﹣∠C＝90°﹣α+β．根据全等三角形对应角相等求出∠DEF＝∠C＝90°﹣α+β，根据∠BED＝∠BEF﹣∠DEF即可得出答案．
【解答】解：∵FH⊥BC，垂足为E，
∴∠CEH＝∠BEF＝90°，
∴∠C＝90°﹣∠CHE＝90°﹣β，
∴∠B＝180°﹣∠A﹣∠C＝180°﹣α﹣（90°﹣β）＝90°﹣α+β．
∵△ABC≌△DEF，
∴∠DEF＝∠B＝90°﹣α+β，
∴∠BED＝∠BEF﹣∠DEF＝90°﹣（90°﹣α+β）＝α﹣β．
故选：A．
【点评】本题考查了全等三角形的性质，垂直的定义，直角三角形的性质，三角形内角和定理．掌握相关性质与定理是解题的关键．
二、填空题（本题共6小题，每小题3分，共18分）
11．（3分）如图，△ABC中，∠B＝35°，∠ACD＝120°，则∠A＝ 85° ．
【分析】根据三角形外角的性质，得∠ACD＝∠B+∠A，那么∠A＝∠ACD﹣∠B＝85°．
【解答】解：∵∠ACD＝∠B+∠A，
∴∠A＝∠ACD﹣∠B＝120°﹣35°＝85°．
故答案为：85°．
【点评】本题主要考查三角形外角的性质，熟练掌握三角形外角的性质是解决本题的关键．
12．（3分）如图，四边形ABCD是轴对称图形，直线AC是它的对称轴，若∠BAC＝65°，∠B＝50°，则∠BCD的大小为 130° ．
【分析】直接利用轴对称图形的性质得出∠DAC＝∠BAC＝65°，∠D＝∠B＝50°，再结合三角形内角的定理得出答案．
【解答】解：∵四边形ABCD是轴对称图形，直线AC是它的对称轴，
∴∠DAC＝∠BAC＝65°，∠D＝∠B＝50°，
∴∠BCA＝∠DCA＝180°﹣65°﹣50°＝65°，
∴∠BCD的大小为：65°×2＝130°．
故答案为：130°．
【点评】此题主要考查了轴对称图形的性质，正确得出对应角度数是解题关键．
13．（3分）一个n边形的每个内角都等于144°，则n＝ 10 ．
【分析】根据多边形的内角和定理：（n﹣2）180°求解即可．
【解答】解：由题意可得：（n﹣2）180°＝n×144°，
解得n＝10．
故答案为：10．
【点评】本题主要考查了多边形的内角和定理．熟练掌握n边形的内角和为：（n﹣2）180°是关键．
14．（3分）如图，在△ABC中，∠B＝∠C＝30°，AD⊥AB交BC于点D，BC＝6，则AD＝ 2 ．
【分析】由三角形的内角和定理可求∠BAC＝120°，结合垂直的定义可求得∠CAD＝30°，BD＝2AD，进而可求得AD＝BC＝2，即可求解．
【解答】解：∵∠B＝∠C＝30°，
∴∠BAC＝180°﹣30°﹣30°＝120°，
∵AD⊥AB，
∴∠BAD＝90°，
∴∠CAD＝∠C＝30°，BD＝2AD，
∴AD＝CD，
∴AD＝BC＝2．
故答案为：2．
【点评】本题主要考查等腰三角形的性质，三角形的内角和定理，含30°角的直角三角形的性质，证明AD＝CD是解题的关键．
15．（3分）如图，在△ABC中，AB＝AC．过点A作BC的平行线交∠ABC的角平分线于点D，连接CD．若∠BAD＝140°，则∠ACD＝ 70 °．
【分析】根据平行线的性质以及角平分线的性质得出AB＝AD，进而得出AC＝AD，进而得出∠DAC＝∠ACB＝40°，根据三角形内角和定理即可求解．
【解答】解：∵∠BAD＝140°，AD∥BC，
∴∠ABC＝40°，
∵AB＝AC，
∴∠ACB＝∠ABC＝40°，
∵AD∥BC，
∴∠DAC＝∠ACB＝40°，
∵BD是∠ABC的角平分线，
∴∠ABD＝∠DBC，
∵AD∥BC，
∴∠ADB＝∠DBC＝20°，
∴∠ABD＝∠ADB＝20°，
∴AB＝AD，
∴AC＝AD，
∴∠ACD＝×（180°−∠CAD）＝×（180°−40°）＝70°．
故答案为：70．
【点评】本题考查了三角形内角和定理，三角形角平分线的定义，平行线的性质，等腰三角形的性质与判定，证明AC＝AD是解题的关键．
16．（3分）如图，在等边△ABC中，BF是AC上中线且BF＝4，点D在线段BF上，连接AD，在AD的右侧作等边△ADE，连接EF，则AE+EF的最小值为 +4 ．
【分析】根据等边三角形的性质可得AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，据此得出∠ABD＝∠ACE，作点A关于CE的对称点M，连接FM交CE于E′，此时AE+EF的值最小，此时AE+EF＝FM，证明△ACM是等边三角形，得出FM＝FB＝4，于是得到结论．
【解答】解：∵△ABC、△ADE都是等边三角形，
∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝60°，
∴∠BAD＝∠CAE，
∴△BAD≌△CAE（SAS），
∴∠ABD＝∠ACE，
∵AF＝CF，
∴∠ABD＝∠CBD＝∠ACE＝30°，
∴点E在射线CE上运动（∠ACE＝30°），
作点A关于CE的对称点M，连接FM交CE于E′，
此时AE+EF的值最小，此时AE+EF＝FM，
∵CA＝CM，∠ACM＝60°，
∴△ACM是等边三角形，
∴△ACM≌△ACB，
∴FM＝FB＝4，
∴AB＝，
∴AE+EF的最小值是AF+FM＝+4，
故答案为：+4．
【点评】本题考查的是轴对称的性质﹣最短路径问题，掌握轴对称的性质、等边三角形的判定和性质是解题的关键．
三、解答题（本题共4小题，其中17题6分，18、19、20题各8分，共30分）
17．（6分）如图，点A，B，C，D在同一条直线上，CE∥DF，EC＝BD，AC＝FD．求证：AE＝FB．
【分析】根据CE∥DF，可得∠ACE＝∠D，再利用SAS证明△ACE≌△FDB，得出对应边相等即可．
【解答】证明：∵CE∥DF，
∴∠ACE＝∠D，
在△ACE和△FDB中，
，
∴△ACE≌△FDB（SAS），
∴AE＝FB．
【点评】此题主要考查全等三角形的判定与性质和平行线的性质；熟练掌握平行线的性质，证明三角形全等是解决问题的关键．
18．（8分）如图，在△ABC中，AB＝AC，D为BC边上一点，AD＝BD，AC＝DC．求∠BAC的度数．
【分析】设∠B＝α，根据等腰三角形的性质得∠B＝∠C＝α，∠B＝∠BAD＝α，进而得∠CDA＝∠B+∠BAD＝2α，则∠CAD＝∠CDA＝2α，∠BAC＝3α，进而根据∠C+∠CAD+∠CDA＝180°可解得α＝36°，据此可得∠BAC的度数．
【解答】解：设∠B＝α，
∵AB＝AC，
∴∠B＝∠C＝α，
∵AD＝BD，
∴∠B＝∠BAD＝α，
∴∠CDA＝∠B+∠BAD＝2α，
∵AC＝CD，
∴∠CAD＝∠CDA＝2α，
∴∠BAC＝∠BAD+∠CAD＝3α，
在△CAD中，∠C+∠CAD+∠CDA＝180°，
∴α+2α+2α＝180°，
解得：α＝36°，
∴∠BAC＝3α＝3×36°＝108°．
【点评】此题主要考查了等腰三角形的性质，三角形内角和定理，熟练掌握等腰三角形的性质，灵活三角形内角和定理进行角度计算是解决问题的关键
19．（8分）如图为某单摆装置示意图，摆线长OA＝OB＝OC，当摆线位于OB位置时，过点B作BD⊥OA于点D，测得OD＝15cm，当摆线位于OC位置时，OB与OC恰好垂直，求此时摆球到OA的水平距离CE的长（CE⊥OA）．
【分析】利用AAS证明△COE≌△OBD，得CE＝OD＝15cm．
【解答】解：∵OB⊥OC，
∴∠BOD+∠COE＝90°，
∵CE⊥OA，BD⊥OA，
∴∠CEO＝∠ODB＝90°，
∴∠BOD+∠B＝90°，
∴∠COE＝∠B，
在△COE和△OBD中，
，
∴△COE≌△OBD（AAS），
∴CE＝OD＝15cm，
∴摆球到OA的水平距离CE的长为15cm．
【点评】本题主要考查了全等三角形的判定与性质，证明△COE≌△OBD是解题的关键．
20．（8分）如答题卡中的图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．
（1）请以x轴为对称轴，画出与△ABC对称的△A1B1C1，并直接写出点A1、B1、C1的坐标；
（2）点P（a+1，b﹣2）与点C关于y轴对称，则a＝ ﹣5 ，b＝ 1 ．
【分析】（1）根据轴对称的性质作图，即可得出答案．
（2）关于y轴对称的点的横坐标互为相反数，纵坐标相等，由此可得a+1＝﹣4，b﹣2＝﹣1，求出a，b的值即可．
【解答】解：（1）如图，ΔA1B1C1 即为所求．
点A1（1，4），B1（5，4），C1（4，1）．
（2）∵点P与点C关于y轴对称，C（4，﹣1），
∴点P的坐标为（﹣4，﹣1），
∴a+1＝﹣4，b﹣2＝﹣1，
解得a＝﹣5，b＝1．
故答案为：﹣5；1．
【点评】本题考查作图﹣轴对称变换，熟练掌握轴对称的性质是解答本题的关键．
四、解答题（本题共2小题，其中21题8分，22题10分，共18分）
21．（8分）如图，在△ABC中，∠BAC的平分线与BC的中垂线DE交于点E，过点E作AC边的垂线，垂足N，过点E作AB延长线的垂线，垂足为M．
（1）求证：BM＝CN；
（2）若AB＝2，AC＝8，求BM的长．
【分析】（1）连接BE，CE，根据角平分线的性质得到EM＝EN，根据线段垂直平分线的性质得到BE＝CE，根据全等三角形的判定和性质即可得到结论；
（2）根据全等三角形的性质得到AM＝AN，设BM＝CN＝x，列方程即可得到结论．
【解答】（1）证明：连接BE，CE，
∵AE平分∠BAC，EM⊥AB，EN⊥AC，
∴EM＝EN，
∵DE垂直平分BC，
∴BE＝CE，
∴Rt△BEM≌Rt△CEN（HL），
∴BM＝CN；
（2）解：∵∠M＝∠ANE＝90°，
∴Rt△AME≌Rt△ANE（HL），
∴AM＝AN，
设BM＝CN＝x，
∵AB＝2，AC＝8，
∴x+2＝8﹣x，
∴x＝3，
∴BM＝3．
【点评】本题考查了全等三角形的判定和性质，角平分线的性质，线段垂直平分线的性质，正确的作出辅助线构造全等三角形是解题的关键．
22．（10分）已知：如图，AC∥BD，请先作图再解决问题．
（1）利用尺规完成以下作图，并保留作图痕迹，（不要求写作法）
①作BE平分∠ABD交AC于点E；
②在BA的延长线上截取AF＝BA，连接EF；
（2）判断△BEF的形状，并说明理由．
【分析】（1）①根据要求作出图形即可；
②根据要求作出图形即可；
（2）证明AE＝AF＝AB，再利用等腰三角形的性质以及三角形内角和定理证明即可．
【解答】解：（1）①如图，射线BE即为所求；
②如图，线段AE，EF即为所求；
（2）△BEF是直角三角形．
理由：∵BE平分∠ABC，
∴∠ABE＝∠EBD，
∵AC∥BD，
∴∠AEB＝∠EBD，
∴∠ABE＝∠AEB，
∴AB＝AE，
∵AB＝AF，
∴AE＝AF＝AB，
∴∠AFE＝∠AEF，∠ABE＝∠AEB，
∵∠ABE+∠AFE+∠BEF＝180°，
∴2∠AEF+2∠AEB＝180°，
∴∠AEF+∠AEB＝90°，
∴∠BEF＝90°，
∴△BEF是直角三角形．
【点评】本题考查作图﹣复杂作图，直角三角形的判定，等腰三角形的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
五、解答题（本题共2小题，其中23题10分，24题12分，共22分）
23．（10分）如图，长方形ABCD中，AB＝4cm，BC＝6cm，现有一动点P从A出发以2cm/秒的速度，沿矩形的边A﹣B﹣C﹣D﹣A返回到点A停止，设点P运动的时间为t秒．
（1）当t＝3时，BP＝ 2 cm；
（2）当t为何值时，连接CP，DP，△CDP是等腰三角形；
（3）Q为AD边上的点，且DQ＝5，当t为何值时，以长方形的两个顶点及点P为顶点的三角形与△DCQ全等．
【分析】（1）当t＝3时，点P运动到线段BC上，即可得到BP的长度；
（2）分三种情况讨论，①当点P在AB上时，②当点P在BC上时，③当点P在AD上时，根据全等三角形的判定与性质、等腰三角形的性质即可得到答案；
（3）根据题意，要使一个三角形与△DCQ全等，则点P的位置可以有四个，根据点P运动的位置，即可计算出时间．
【解答】解：（1）当t＝3时，点P走过的路程为：2×3＝6，
∵AB＝4，
∴点P运动到线段BC上，
∴BP＝6﹣4＝2，
故答案为：2；
（2）①当点P在AB上时，△CDP是等腰三角形，
∴PD＝CP，
在矩形ABCD中，AD＝BC，∠A＝∠B＝90°，
∴△DAP≌△CBP（HL），
∴AP＝BP，
∴AP＝＝2，
∴t＝＝1，
②当点P在BC上时，△CDP是等腰三角形，
∵∠C＝90°，
∴CD＝CP＝4，
∴BP＝CB﹣CD＝2，
∴t＝＝3，
③当点P在AD上时，△CDP是等腰三角形，
∵∠D＝90°，
∴DP＝CD＝4，
∴t＝＝9，
综上所述，t＝1或3或9时，△CDP是等腰三角形；
（3）根据题意，如图，连接CQ，则AB＝CD＝4，∠A＝∠B＝∠C＝∠D＝90，DQ＝5，
∴要使一个三角形与△DCQ全等，则另一条直角边必须等于DQ，
①当点P运动到P1时，CP1＝DQ＝5，此时△DCQ≌△CDP1，
∴点P的路程为：AB+BP1＝4+1＝5，
∴t＝5÷2＝2.5，
②当点P运动到P2时，BP2＝DQ＝5，此时△CDQ≌△ABP2，
∴点P的路程为：AB+BP2＝4+5＝9，
∴t＝9÷2＝4.5，
③当点P运动到P3时，AP3＝DQ＝5，此时△CDQ≌△ABP3，
∴点P的路程为：AB+BC+CD+DP3＝4+6+4+1＝15，
∴t＝15÷2＝7.5，
④当点P运动到P4时，即P与Q重合时，DP4＝DQ＝5，此时△CDQ≌△CDP4，
∴点P的路程为：AB+BC+CD+DP4＝4+6+4+5＝19，
∴t＝19÷2＝9.5，
综上所述，时间的值可以是：t＝2.5，4.5，7.5或9.5，
故答案为：2.5或4.5或7.5或9.5．
【点评】本题考查了全等三角形的判定与性质，等腰三角形的性质，矩形的性质，线段的动点问题，解题的关键是掌握全等三角形的判定与性质及动点的运动状态，从而进行分类讨论．
24．（12分）在△ABC中，AB＝AC，∠BAC＝α，射线AD，AE的夹角为，过点B作BF⊥AD于点F，直线BF交AE于点G，连结CG．
（1）如图1，射线AD，AE都在∠BAC内部．
①若α＝120°，∠CAE＝20°，则∠CBG＝ 20 °；
②作点B关于直线AD的对称点H，在图1中找出与线段GH相等的线段，并证明．
（2）如图2，射线AD在∠BAC的内部，射线AE在∠BAC的外部，其它条件不变，探究线段BF，BG，CG之间的数量关系，并证明．
【分析】（1）①先根据角的运算得出∠BAD的度数，根据三角形内角和求出∠ABC的度数；再根据直角三角形两锐角互余可得出∠ABG的度数，作差可得结论；
②连接AH，可得出AB＝AH＝AC，再根据∠BAC＝α，∠DAE＝α，可得出∠BAF+∠CAE＝α，∠HAF+∠HAG＝α，所以∠CAE＝∠HAG；进而可得△AGH≌△AGC（SAS），再由全等三角形的性质可得结论；
（2）在BG延长线上取点H，使HF＝BF．连结AH．由垂直平分线的性质可得AB＝AH，∠BAF＝∠HAF；设∠CAD＝x，∠CAE＝y，所以∠DAE＝x+y，由此表达∠BAC，∠BAF，∠HAF，由∠HAE＝∠DAE+∠HAE，可得x+2y＝x+y+∠HAE，所以∠HAE＝y，即∠HAE＝∠CAE；由此可得△ACG≌△AHG（SAS），所以CG＝HG，由此可得结论．
【解答】解：（1）①∵∠BAC＝α＝120°，∠DAE＝α＝60°，∠CAE＝20°，
∴∠BAD＝120°﹣60°﹣20°＝40°，
∵BF⊥AD，
∴∠AFB＝90°，
∴∠ABF＝90°﹣40°＝50°，
∵AB＝AC，
∴∠ABC＝∠ACB，
∴∠ABC＝30°，
∴∠CBG＝∠ABF﹣∠ABC＝50°﹣30°＝20°；
故答案为：20．
②GH＝GC，理由如下：
证明：如图1，连结AH，
∵点B与点H关于直线AD对称，AF⊥BH，
∴BF＝HF，
∴AD是BH的垂直平分线，
∴AB＝AH，∠BAF＝∠HAF，
∵AB＝AC，
∴AH＝AC，
∵∠BAC＝α，∠DAE＝α，
∴∠BAF+∠CAE＝α，∠HAF+∠HAG＝α，
∴∠CAE＝∠HAG；
∵AG＝AG，
∴△AGH≌△AGC（SAS）．
∴GH＝GC；
（2）BG＝2BF﹣CG；
证明：如图2，在BG延长线上取点H，使HF＝BF．连结AH．
∵AF⊥BH，BF＝HF，
∴AB＝AH，∠BAF＝∠HAF；
设∠CAD＝x，∠CAE＝y，
∴∠DAE＝x+y，
∵∠DAE＝∠BAC．
∴∠BAC＝2x+2y，
∴∠BAF＝∠BAC﹣∠CAD＝2x+2y﹣x＝x+2y．
∴∠HAF＝∠BAF＝x+2y，
∵∠HAE＝∠DAE+∠HAE，
∴x+2y＝x+y+∠HAE，
∴∠HAE＝y，即∠HAE＝∠CAE；
∵AB＝AC，AB＝AH，
∴AC＝AH，
∵AG＝AG．
∴△ACG≌△AHG（SAS）．
∴CG＝HG；
∵BG＝BH﹣GH，BH＝2BF，
∴BG＝2BF﹣CG．
【点评】本题在三角形背景下考查旋转的相关知识，属于三角形的综合应用，熟练掌握三角形全等的判定及性质，轴对称的性质是解题的关键．
六、解答题（本题12分）
25．（12分）综合与实践
阅读材料：
材料1：如图1，在Rt△ABC中，∠ACB＝90°，∠A＝60°，以C为圆心，CA长为半径画弧，交AB边于点D，连结CD，则△ACD是等边三角形，△BCD是等腰三角形．
材料2：如图2，△ABC是等边三角形，D为直线BD上一点，以AD为边在AD右侧作等边△ADE，连结CE，随着D点位置的改变，始终有△ABD≌△ACE．
根据上述阅读材料，解决下面的问题．
已知，在△ABC中，∠ACB＝90°，∠A＝60°，D为AB边上一点，以CD为边在CD右侧作等边△CDE．
特例探究：（1）如图3，当点E在AB边上时，求证：DE＝BE．
感悟应用：（2）如图4，当点E在△ABC内部时，连结BE，求证：DE＝BE．
拓展延伸：（3）当点E在△ABC的外部时，过点E作EH⊥AB于H，EF∥AB交射线AC于F，CF＝2，BH＝3，请画出图形，并求AB的长．
【分析】（1）根据题意可得∠B＝30°，结合△CDE是等边三角形即可求出∠BDE＝∠B，从而得证．
（2）以C为圆心，CA长为半径画弧交AB边于点M，连接CM，EM，则CM＝CA，即可得出△ACM是等边三角形，然后证明△ACD≌△MCE，△MCE≌△MBE 即可得证；
（3）分两种情况进行讨论，当点F在线段AC上时和点F在AC延长线上时，分别计算即可．
【解答】（1）证明：在△ABC中，∠ACB＝90°，∠A＝60°，
∴∠B＝30°，
∵△CDE是等边三角形，
∴∠CED＝60°，
∵∠CED＝∠B+∠BDE，
∴∠BDE＝60°﹣30°＝30°，
∴∠BDE＝∠B，
∴DE＝BE．
（2）解：如图，以C为圆心，CA长为半径画弧交AB边于点M，连接CM，EM，则CM＝CA，
∵∠A＝60°，
∴△ACM是等边三角形，
∴∠ACM＝∠AMC＝60°，
又∵△CDE是等边三角形，
∴CD＝CE，∠DCE＝60°，
∴∠ACM＝∠DCE，
∴∠ACM﹣∠DCM＝∠DCE﹣∠DCM，即∠ACD＝∠MCE，
∴△ACD≌△MCE（SAS），
∴∠CME＝∠A＝60°，
∵∠AMC＝60°，
∴∠BME＝180°﹣∠AMC﹣∠CME＝180°﹣60°﹣60＝60°，
∴∠CME＝∠BME，
∵∠BCM＝∠ACB﹣∠ACM＝90°﹣60°＝30°，
∴∠BCM＝∠ABC，
∴MC＝MB，
又∵ME＝ME，
∴△MCE≌△MBE （SAS），
∴CE＝BE，
又∵△CDE是等边三角形，
∴CE＝DE，
∴DE＝BE．
（3）解：如图，当点F在线段AC上时，以C为圆心，CA长为半径画弧，交AB边于M，连结ME，BE，CM，则△ACM为等边三角形，
∴△ACD≌△MCE（SAS），
∴∠CME＝∠A＝60°，∠EMB＝60°＝∠CME，
又∵CM＝BM，
∴△CME≌△BME（SAS），
∴BE＝CE，
∵CE＝DE，
∴BE＝DE，
∵EH⊥BD，
∴BD＝2BH，
∵BH＝3，
∴BD＝6，
∵EF∥AB，
∴∠CFE＝∠A＝60°，
∴∠CFE＝∠CMA．
∵∠ECF＝∠ECD+∠ACD＝60°+∠ACD，∠CDM＝∠A+∠ACD＝60°+∠ACD，
∴∠ECF＝∠CDM，
又∵∠ECF＝∠CDM，
∴△ECF≌△CDM（SAS），
∴DM＝CF＝2，
∴BM＝BD﹣DM＝6﹣2＝4，
∵CM＝AM，CM＝BM，
∴AM＝BM，
∴AB＝2BM＝8；
如图，当点F在AC延长线上时，同理可得 BD＝2BH＝6．
∵EF∥AB，
∴∠F+∠A＝180°，
∴∠F＝120°，
∵∠AMC＝60°，
∴∠CMD＝120°，
∴∠F＝∠CMD．
∵∠ACM＝∠DCE＝60°，
∴∠FCE+∠MCD＝180°﹣120°＝60°，∠MCD+∠MDC＝∠AMC＝60°．
∴∠FCE＝∠MDC．
又∵CD＝CE，
∴△FCE≌△MDC（AAS），
∴MD＝FC＝2，
∴MB＝BD+MD＝8．同理AM＝BM＝8，
∴AB＝2AM＝16．
综上所述，AB的长为8或16．
【点评】本题考查等边三角形的判定和性质，全等三角形的判定和性质，正确作出辅助线是解题关键．