浙江省台州市温岭市第三中学2023-2024学年上学期期中考试九年级数学试卷（含答案）

这是一份浙江省台州市温岭市第三中学2023-2024学年上学期期中考试九年级数学试卷（含答案），文件包含参考答案2023doc、市三中2023学年第一学期九年级期中测试修改2docx、参考答案2023pdf、市三中2023学年第一学期九年级阶段性测试数学答题卷1pdf等4份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。

一．选择题（本大题共10小题，每小题3分，共30分）
1．将方程2x2＝7x﹣3化为一般形式后，常数项为3，则一次项系数为（ ）
A．7B．﹣7C．7xD．﹣7x
2．将四个数字看作一个图形，则下列四个图形中，是中心对称图形的是（ ）
A． B． C． D．
3．关于二次函数y＝﹣3（x﹣1）2+2，下列说法正确的是（ ）
A．开口向上 B．当x＞1时，y随x的增大而增大 C．有最小值2 D．顶点坐标是（1，2）
4．如图，AB是⊙O的直径，C，D是⊙O上两点，若∠AOC＝140°，则∠BDC＝（ ）
A．20°B．40°C．55°D．70°
（第4题图） （第7题图） （第9题图）
5．一元二次方程3x2+4x﹣1＝0的根的情况为（ ）
A．有两个相等的实数根 B．有两个不相等的实数根 C．没有实数根 D．无法确定
6．抛物线y＝2（x+1）2﹣4平移后，得到抛物线，y＝2x2，则平移方法是（ ）
A．先向左平移1个单位，再向上平移4个单位B．先向左平移1个单位，再向下平移4个单位
C．先向右平移1个单位，再向上平移4个单位D．先向右平移1个单位，再向下平移4个单位
7．如图，△ABC中∠BAC＝100°，将△ABC绕点A逆时针旋转150°，得到△ADE，这时点B、C、D恰好在同一直线上，则∠E的度数为（ ）
A．50°B．75°C．65°D．60°
8．某小区新增了一家快递店，第一天揽件200件，到第三天统计得出三天共揽件662件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（ ）
A．200（1+x）2＝662 B．200（1+2x）2＝662
C．200（1﹣x）2＝662 D．200+200（1+x）+200（1+x）2＝662
9．如图，△ABC的顶点均在⊙O上，且AB＝AC，∠BAC＝120°，D为弦BC的中点，弦EF经过点D，且EF∥AB．若⊙O的半径为4，则弦EF的长是（ ）
A．3B．2C．2D．2
10．将抛物线y＝x2+x﹣6位于y轴左侧的部分沿x轴翻折，其余部分不变，翻折得到的图象和原来不变的部分构成一个新图象，若直线与新图象有且只有2个公共点，则t的取值范围是（ ）
A．﹣6< t ≤6 B．﹣6< t <6 C．或﹣6≤ t <6 D．或﹣6≤ t ≤6
二．填空题（本大题共6小题，每小题4分，共24分）
11．已知A（a，1）与B（5，b）关于原点对称，则a﹣b＝ ．
12．若x1、x2是一元二次方程x2+2x＝3的两根，则x1•x2的值是 ．
13．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，将△ABC绕点C顺时针旋转得到△A'B'C，其中点A'与点A是对应点，点B'与点B是对应点，若点B'恰好落在AB边上，则点A到直线A'C的距离等于 ．
（第13题图） （第14题图） （第16题图）
14．如图，一条笔直铁路MN和一条笔直公路PQ在点O处交汇，∠QON＝30°，在点A处有一栋居民楼，OA＝200米，已知火车行驶时，周围200米以内都会受到噪声的影响，若火车在铁路MN上沿ON方向以每秒20米的速度行驶，那么居民楼受噪声影响的时间为 秒．（不考虑火车长度，结果保留小数点后一位，参考数据：≈1.414，≈1.732）
15．已知抛物线y＝ax2+bx+c（a，b，c为常数且a≠0）图象经过P1（﹣1，y1），P2（1，y2），P3（4，y3），P4（5，y4）四点，若0＜y4＜y1＜y3，则下列结论：①a＜0；②b2﹣4ac＞0；③﹣4a＞b＞﹣3a；④y2＜y3．其中一定正确的是 .（填序号）
16．如图，在平面直角坐标系中，点P是以C（-1.5，2）为圆心，1为半径的⊙C上的一个动点，已知A（﹣1，0），B（1，0），连接PA，PB，则PA2+PB2的最小值是 ．
三．解答题（共8 题，第17~19 题每题6分，第20~22题每题8分，第23~24 题每题12分，共66分）
17．解方程:（x+4）2＝5（x+4）．
18．如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的顶点均在格点上．
（1）画出将△ABC关于原点O的中心对称图形△A1B1C1．
（2）将△DEF绕点E逆时针旋转90°得到△D1EF1，画出△D1EF1．
（3）若△DEF由△ABC绕着某点旋转得到的，则这点的坐标为 ．
(第18题图）
19．定义：若一元二次方程ax2+bx+c＝0（a≠0）满足b＝ac．则称此方程为“和美”方程．
（1）当b＜0时，判断此时“和美”方程ax2+bx+c＝0（a≠0）解的情况，并说明理由．
（2）若“和美”方程2x2+mx+n＝0 有两个相等的实数根，请解出此方程．
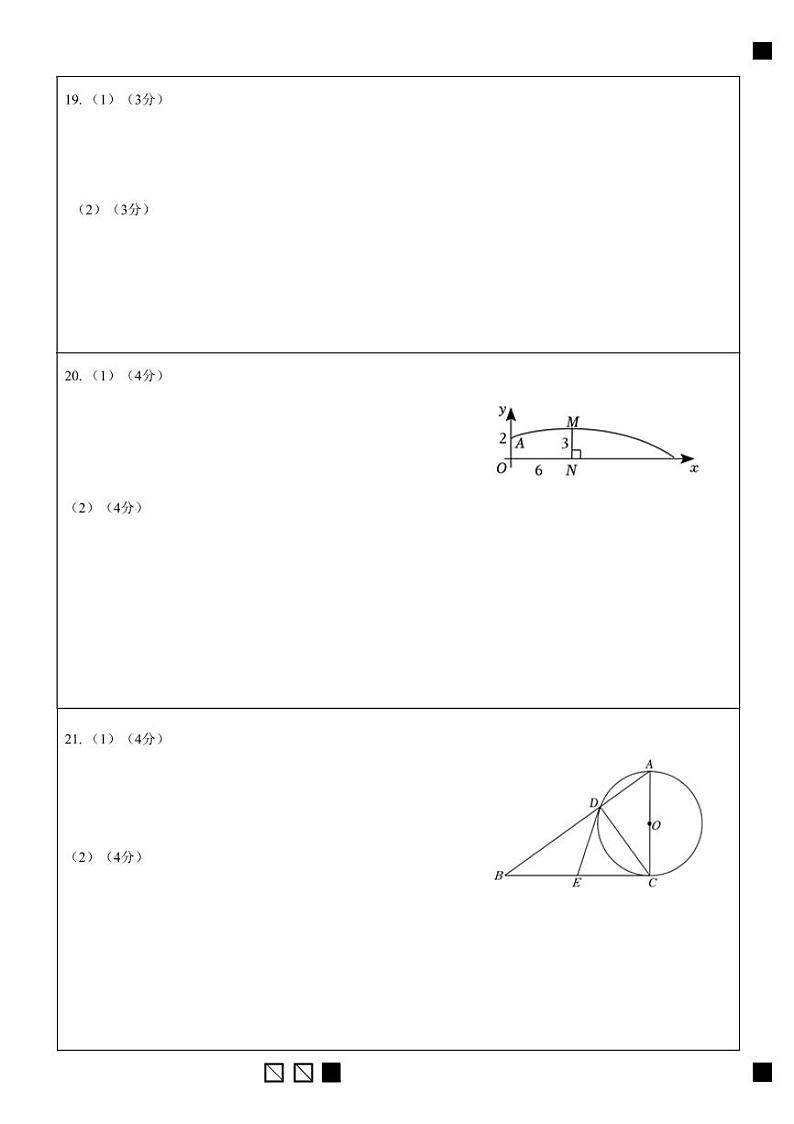
20．如图，杭州亚运会上某运动员站在点O处练习发排球，将球从O点正上2m的A点处发出，把球看成点，其运行的路线近似看作是抛物线的一部分．已知球与O点的水平距离ON为6m时，达到最高3m，球场的边界距O点的水平距离为18m．
（1）请确定排球运行的高度y（m）与运行的水平距离x（m）满足的函数关系式；
（2）请判断排球第一次落地是否出界？请通过计算说明理由．

（第20题图）

21．如图，在Rt△ABC中，∠ACB＝90°，E是BC的中点，以AC为直径的⊙O与AB边交于点D，连接DE．
（1）求证：DE是⊙O的切线；
（2）若CD＝3cm，DE＝2.5cm，求⊙O直径的长．
（第21题图）
22．如图，在正方形ABCD中，线段CD绕点C逆时针旋转到CE处，旋转角为α（0°＜α＜90°），点F在直线DE上，且AD＝AF，连接BF．
（1）求∠BAF的大小（用含α的式子表示）．
（2）求证：EF＝BF．
（第22题图）
23．在直角坐标系中，设函数y＝ax2+bx+c（a，b，c是常数，a≠0）．
（1）已知a＝1．
①若函数的图象经过（0，3）和（﹣1，0）两点，求函数的表达式；
②若将函数图象向下平移两个单位后与x轴恰好有一个交点，求b+c的最小值．
（2）若b=a+1，（x1，y1），（x2，y2）是该函数图象上的两个不同点,对于任意x1、x2，当x1＞x2 ≥﹣3时，恒有y1＞y2，试求a的取值范围．
24．如图1，扇形AOB中，∠AOB＝90°，OA＝6，点P在半径OB上，连接AP．
（1）把△AOP沿AP翻折，点O的对称点为点Q．
①当点Q刚好落在弧AB上，求弧AQ的长；
②如图2，点Q落在扇形AOB外，AQ与弧AB交于点C，过点Q作QH⊥OA，垂足为H，
探究OH、AH、QC之间的数量关系，并说明理由；
（2）如图3，记扇形AOB在直线AP上方的部分为图形W，把图形W沿着AP翻折，点B的对称点为点E，弧AE与OA交于点F，若OF＝2，求PO的长．
（第24题图）