人教版（中职）基础模块下册8.2 直线的方程说课ppt课件

这是一份人教版（中职）基础模块下册8.2 直线的方程说课ppt课件，共25页。PPT课件主要包含了观察并回答问题，求下列直线的方程，1直线的斜率，2直线的斜率，y＝x＋2，y＝2，x＝4，直线的一般式方程等内容，欢迎下载使用。

1．直线倾斜角的定义及范围是什么？
2．已知 P1(x1，y1) 和 P2(x2，y2) 且 x1≠x2 ，　 则直线的斜率是多少？
一般地，平面直角坐标系内，直线向上的方向与 x 轴正方向所成的最小正角  叫做这条直线的倾斜角．范围是 0≤<180 ．
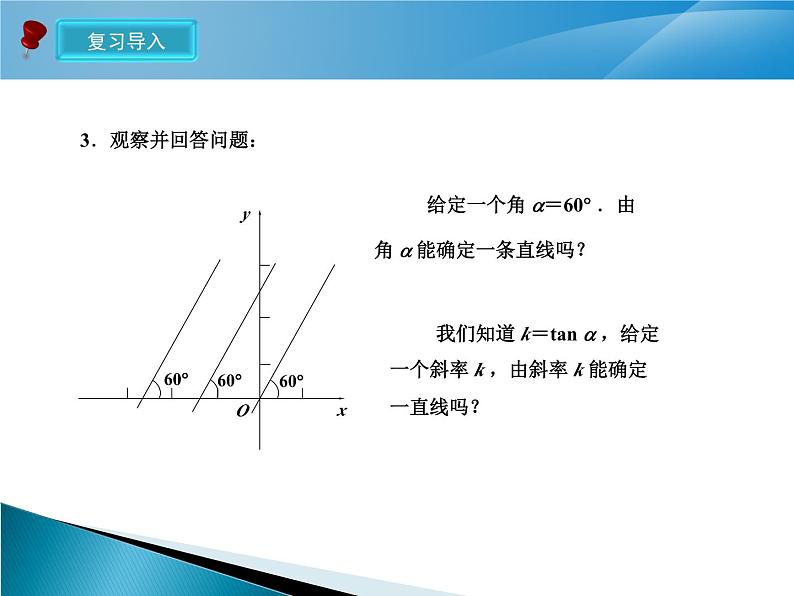
　　给定一个角 ＝60 ．由角  能确定一条直线吗？
　　我们知道 k＝tan  ，给定一个斜率 k ，由斜率 k 能确定一直线吗？
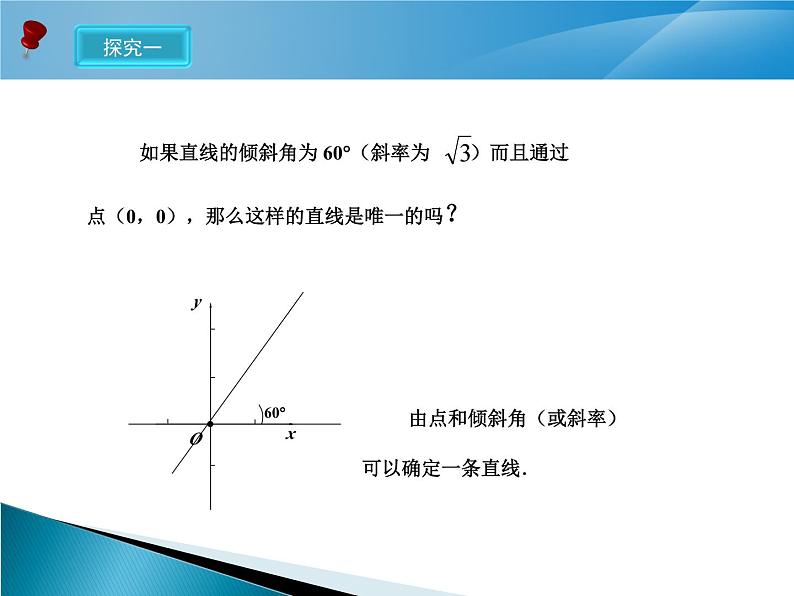
　　由点和倾斜角（或斜率）可以确定一条直线．
　　设直线 l 上不同于 P1 的任意一点的坐标为P(x，y)，由斜率公式得：
经验证：点 (1，2) 符合上式，此方程为所求直线方程．
可化为：y－y0＝k（x－x0）．
若直线 l 经过点 P1（x0，y0），且斜率为 k ，求 l 方程 ．
　　设点 P(x，y) 是直线上不同于点 P1 的任意一点，根据经过两点的直线的斜率公式得
　　我们把方程y－y0＝k（x－x0）叫做直线的点斜式方程．
点斜式方程 　　　　　　y－y0＝k（x－x0）（1）这个方程是由哪两个条件确定的？（2）当直线 l 的倾斜角为 0 时，直线方程为是什么？（3）当直线倾斜角为 90 时，直线有斜率吗？　　 它的方程能用点斜式表示吗？　　 此时直线方程是什么？
（3）b 是直线在 y 轴上的截距．
（1）如果直线的斜率为 k ，直线与 y 轴交点为（0，b），你能写出这条直线的方程吗？是什么？
（2）斜截式方程y＝k x＋b ．
例1　求下列直线的方程（1）过点（0，0），斜率为 2 ；（2）过点（4，5），斜率为 1 ；（3）过点（5，5），倾斜角为 0 ；（4）过点（1，2），倾斜角为 30 ；（5）截距为－3，倾斜角为 45 ．
（1）直线的方程为 y－0＝2(x－0) ，即 y＝2x ．
（3）直线的斜率为 k＝tan 0＝0 ，因此方程为y－5＝0×(x－5) ，即 y＝5 ．
（5）直线的斜率为 k＝tan 45＝1，因此方程为y＝1×x＋（－3），即y＝x－3．
(2)直线的方程为y－5＝1(x－4)，即y＝x+1；
（1）过点（－3，2），斜率为 －1 ； （2）过点（1，2），倾斜角为 60 ；（3）截距为 －2 ，倾斜角为 45 ．
例2　求下列直线的方程：（1）过点（0，0）和（1，5）；（2）过点（5，0）和（0，6）．
所以直线方程为 y－0＝5×(x－0)，即 y＝5 x．
所以由直线方程的斜截式得
　　求过点（－2，2）和（0，－2）的直线方程
1．根据下列条件，写出直线的方程：（1）经过点 A（8，– 2），斜率是 －1； （2）截距是 2 ，斜率为 1 ；（3）经过点 A（4，2），平行于 x 轴；（4）经过点 A（4，2），平行于 y 轴．
2．上述几种形式的直线方程，可以用 A x＋B y＋C＝0来表示吗？
y＋2＝ －(x－8)
　　平面直角坐标系中的每一条直线都可以用一个 关于 x、y 的二元一次方程表示吗？　　对直线的倾斜角  进行讨论： ① 当 ≠90 时， 直线斜率为 k＝tan  ，其方程可　 写成：y＝k x＋b ，可变形为：A x＋B y＋C＝0，　 其中：A = k，B = －1，C = b．② 当 ＝90 时，直线斜率不存在，其方程可写成　 x＝a 的形式，也可以变形为：A x＋B y＋C＝0，　 其中：A＝1，B＝0，C＝－a．　　平面直角坐标系中任何一条直线都可以用关于 x、y 的二元一次方程 A x＋B y＋C＝0（A、B不同时为零）来表示；反之，每一个关于 x、y 的二元一次方程都表示一条直线．
我们把关于 x、y 的二元一次方程 A x＋B y＋C＝0（ A、B 不同时为零 ) 叫做直线的一般式方程．
直线的方向向量与法向量　　
　　（1）如果非零向量　所在的直线与直线l 平行，则称　为直线 l 的一个方向向量；
　　（2）如果非零向量　所在的直线与直线l 垂直，则称　为直线 l 的一个法向量．
（3）直线的方向向量与法向量有怎样的关系？你能找出直线 x＝2 的一个方向向量和一个法向量吗？
　　向量 (x2－x1，y2－y1) 与向量 (1，k) 是什么关系？向量 (1，k) 是直线的一个方向向量吗？
　　（2）令 ＝x2－x1 ，如果 ≠0 ，且直线 l 的斜率为k，由 (x2－x1，y2－y1)＝ (1，　　　)＝ (1，k) ．
　　（1）如果直线 l 过点 P1 (x1 ，y1) 和 P2(x2 ，y2) ，向量 的坐标是多少？它是直线 l 的一个方向向量吗？
　（1）设 l 的一般式方程为A x＋B y＋C＝0，如果 P2(x2，y2) 和 P1(x1，y1) 都在直线上，两点 P2，P1分别满足怎样的关系式？
　（2）把得到的两个关系式相减，你能得到怎样的式子？
　（3）式子 A(x2－x1)＋B(y2－y1)＝0，能说明向量　＝(A，B) 与向量垂直吗？
（4）向量　＝(A，B) 是直线 l的一个法向量吗？
　 如果知道直线的斜截式方程 y＝k x＋b ，则 (1，k)是它的一个方向向量； 如果知道直线的一般式方程 A x＋B y＋C＝0 ，　则 (A，B) 是它的一个法向量．
例3　求下列直线的一般式方程，并指出它的一个方向向量和法向量：（1）过点 (－3，－2) ，且斜率为 －2 ；（2）过点 (5，5)，且倾斜角为 120 ．
（1）直线的点斜式方程为 y－(－2)＝(－2)[x－(－3)]，化简得 y＝ －2 x－8 ，所以该直线的一般式方程为2 x＋y＋8＝0．由上知，(1，－2) 为直线的一个方向向量，　　　　(2，1) 为直线的一个法向量．
（2）因为直线的斜率为 k＝tan120 ＝ －　，所以直线的点斜式方程为 y－5 ＝ － (x－5) ，因此该直线的一般式方程为x＋y－5－5　　＝0．由上知，(1， 　) 为直线的一个方向向量，(　 ，1) 为直线的一个法向量．
　　求下列直线方程的一般式，并指出它的一个方向 向量和法向量： （1）斜率为- ，过点（6，-2）；（2）过点（3，-3）且平行于 x 轴．答案：（1） ，方向向量 ，法向量 （2） ，方向向量 ，法向量
例4　求下列直线的一般式方程：（1）(1，4) 是直线的一个方向向量，且在y轴上的截距为5；（2）(3，4) 是直线的一个法向量，且直线过点(－1，－2)．
（1）由已知可得直线的斜率为 4 ，所以直线的斜截式方程为 y＝4 x＋5 ，因此一般式方程为4 x－y＋5＝0．
（2）由已知可设直线方程为 3 x＋4 y＋C＝0，其中 C 为待定系数．代入点 (－1，－2)，有3×(－1)＋4×(－2)＋C＝0，解得 C＝11 ．因此直线的一般式方程为3 x＋4 y＋11＝0．
2．直线的斜截式方程： 　　　　y＝k x＋b．3．直线一般式方程： A x＋B y＋C＝04.直线的方向向量：如果非零向量　所在的直线与直线 l 平行，则称　为直线 l 的一个方向向量．5.直线的法向量：如果非零向量　所在的直线与直线 l 垂直，则称 为直线 l 的一个法向量．
1．直线点斜式方程： y－y0＝k（x－x0）；