辽宁省营口市大石桥市某校2023-2024学年九年级上学期期中考试数学试题

这是一份辽宁省营口市大石桥市某校2023-2024学年九年级上学期期中考试数学试题，共7页。
一．选择题（共10小题，满分20分，每小题2分）
1．（2分）搭载神舟十六号载人飞船的长征二号F遥十六运载火箭于2023年5月30日成功发射升空，景海鹏、朱杨柱、桂海潮3名航天员开启“太空出差”之旅，展现了中国航天科技的新高度．下列图标中，其文字上方的图案是中心对称图形的是（ ）
A． B． C．D．
2．（2分）关于x的一元二次方程kx2﹣4x+2＝0有实数根，则k的取值范围是（ ）
A．k＝2B．k≥2且k≠0C．k≤2D．k≤2且k≠0
3. （2分）如图，阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形．若点A的坐标是（1，3），则点M和点N的坐标分别是（ ）
A．M（1，﹣3），N（﹣1，﹣3）
B．M（﹣1，﹣3），N（﹣1，3）
C．M（﹣1，﹣3），N（1，﹣3）
D．M（﹣1，3），N（1，﹣3）
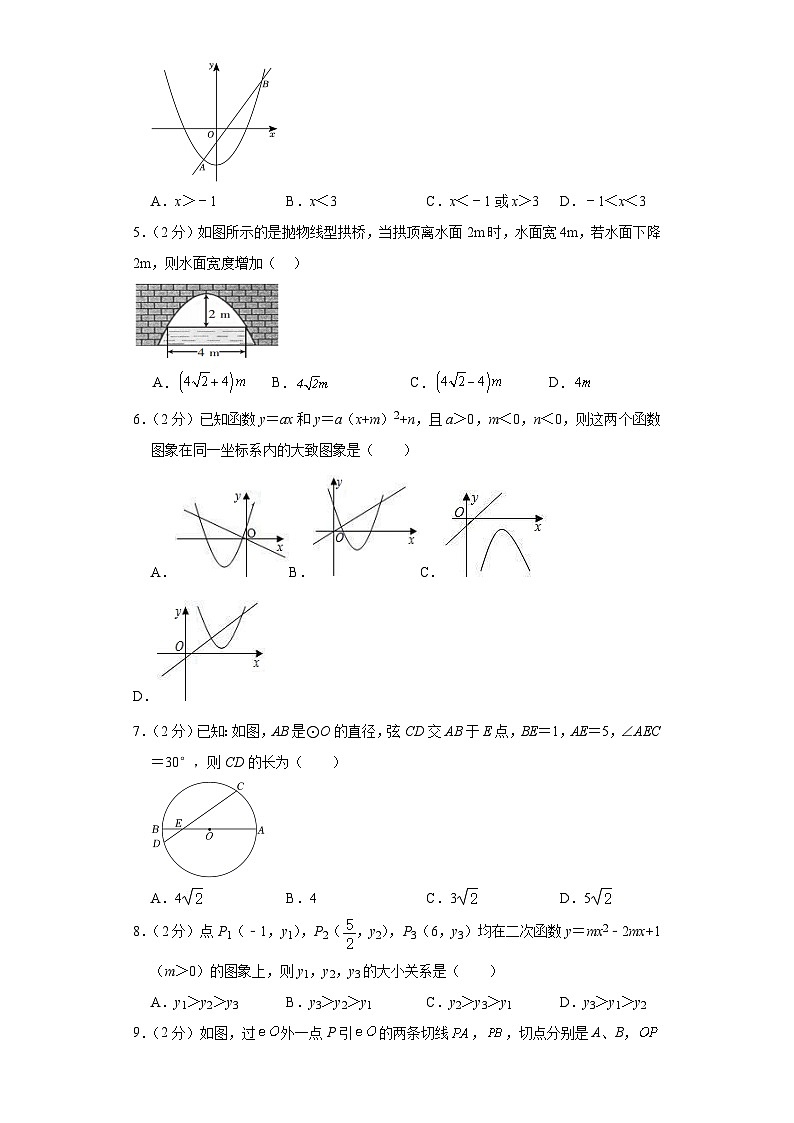
4．（2分）如图，抛物线y＝ax2+c与直线y＝mx+n交于A（﹣1，p），B（3，q）两点，则不等式ax2﹣mx+c＞n的解为（ ）
A．x＞﹣1B．x＜3C．x＜﹣1或x＞3D．﹣1＜x＜3
5．（2分）如图所示的是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，若水面下降2m，则水面宽度增加（ ）
A．B．C．D．
6．（2分）已知函数y＝ax和y＝a（x+m）2+n，且a＞0，m＜0，n＜0，则这两个函数图象在同一坐标系内的大致图象是（ ）
A．B．C．D．
7．（2分）已知：如图，AB是⊙O的直径，弦CD交AB于E点，BE＝1，AE＝5，∠AEC＝30°，则CD的长为（ ）
A．4B．4C．3D．5
8．（2分）点P1（﹣1，y1），P2（，y2），P3（6，y3）均在二次函数y＝mx2﹣2mx+1（m＞0）的图象上，则y1，y2，y3的大小关系是（ ）
A．y1＞y2＞y3B．y3＞y2＞y1C．y2＞y3＞y1D．y3＞y1＞y2
9．（2分）如图，过外一点P引的两条切线，，切点分别是A、B，交于点C，点D是优弧上不与点A、点C重合的一个动点，连接，．若，则的度数是（ ）
A．B．C．D．
10．（2分）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C．下列说法：①abc＜0；②抛物线的对称轴为直线x＝﹣1；③当﹣3＜x＜0时，ax2+bx+c＞0；④当x＞1时，y随x的增大而增大；⑤am2+bm≤a﹣b（m为任意实数），其中正确的个数是（ ）
A．1个B．2个C．3个D．4个
二．填空题（共6小题，满分18分，每小题3分）
11．（3分）关于x的方程（a﹣3）x|a﹣1|+x﹣1＝0是一元二次方程，则a的值是 ．
12．（3分）点P（2a+1，4）与P'（1，3b﹣1）关于原点对称，则2a+b＝ ．
13．（3分）已知AB，CD是⊙O的两条平行弦，AB＝24，CD＝10，⊙O的半径为13，则弦AB与CD的距离为 ．
14．（3分）如图，用一个半径为20cm，面积为的扇形铁皮，制作一个无底的圆锥不计接头损耗，则圆锥的底面半径r为______cm．
15．（3分）底面半径为3cm，母线长为5cm的圆锥的侧面积为 cm2．
16．（3分）如图，抛物线y＝x2﹣4与x轴交于A、B两点，P是以点C（0，3）为圆心，2为半径的圆上的动点，Q是线段PA的中点，连接OQ．则线段OQ的最大值是 ．
三．解答题（共9小题，满分82分）
17．（6分）解方程：1）2（x-1）2=1- x； 2)．
18．（8分）已知一元二次方程x2﹣（2k+1）x+k2+k＝0．
（1）求证：方程有两个不相等的实数根；
（2）若△ABC的两边AB、AC的长是这个方程的两个实数根，第三边BC的长为4，当△ABC是等腰三角形时，求k的值．
19．（8分）如图，△ABC的三个顶点的坐标分别为A（﹣2，3），B（﹣4，1），C（﹣1，2）．
（1）作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1；
（2）作出△ABC关于原点O成中心对称的△A2B2C2，写出B2和C2的坐标；
（3）直接写出△ABC绕原点O顺时针旋转一周扫过的图形面积．
20．（8分）掷实心球是河南高中阶段学校招生体育考试的选考项目.如图1所示的是一名女生在投实心球，实心球行进路线可近似地看作一条抛物线，行进高度y（m）与水平距离x（m）之间的函数关系如图2所示，掷出时起点处高度为，当水平距离为时，实心球行进至最高点处.
(1)求y关于x的函数表达式.
(2)根据河南高中阶段学校招生体育考试评分标准（女生），投掷过程中，当实心球从起点到落地点的水平距离大于等于m时，此项考试得分为满分分.该女生在此项考试中是否得满分？请说明理由.（）
21．（8分）如图，在中，，点P从点A开始沿边向终点B以1的速度移动．与此同时，点Q从点B开始沿边向终点C以2的速度移动．点P、Q分别从点A，B同时出发，当点Q移动到点C时，两点停止移动．设移动时间为t．（）

(1)填空：____________，____________（用含t的代数式表示）．
(2)是否存在t的值，使得的面积为4？若存在请求出此时t的值；若不存在，请说明理由．
22．（10分）某品牌大米远近闻名，深受广大消费者喜爱，某超市每天购进一批成本价为每千克4元的该大米，以不低于成本价且不超过每千克7元的价格销售．当每千克售价为5元时，每天售出大米950kg；当每千克售价为6元时，每天售出大米900kg，通过分析销售数据发现：每天销售大米的数量y（kg）与每千克售价x（元）满足一次函数关系．
（1）请直接写出y与x的函数关系式；
（2）超市将该大米每千克售价定为多少元时，每天销售该大米的利润可达到1800元？
（3）当每千克售价定为多少元时，每天获利最大？最大利润为多少？
23．（10分）．如图，AB是⊙O的直径，点C，D是⊙O上AB异侧的两点，DE⊥CB，交CB的延长线于点E，且BD平分∠ABE．
（1）求证：DE是⊙O的切线．
（2）若∠ABC＝60°，AB＝4，求图中阴影部分的面积．
24．（12分）如图1，Rt△ABF≌Rt△CBE，∠ABC＝90°，点E，F分别在边AB，BC上，点M为AF中点．
（1）请直接写出线段CE与BM的关系；
（2）连接EF，将△EBF绕点B逆时针旋转至如图2位置，请写出CE与BM的关系，并说明理由；
（3）在△EBF绕点B旋转的过程中，当B，C，E三点共线时，若BC＝3，EF＝，请直接写出CM的长．
25．（12分）如图，在平面直角坐标系中，二次函数y＝﹣x2+bx﹣c的图象与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C．
（1）求这个二次函数的表达式．
（2）如图1，二次函数图象的对称轴与直线AC：y＝x+3交于点D，若点M是直线AC上方抛物线上的一个动点，求△MCD面积的最大值．
（3）如图2，点P是直线AC上的一个动点，过点P的直线l与BC平行，则在直线l上是否存在点Q，使点B与点P关于直线CQ对称？若存在，请直接写出点Q的坐标；若不存在，请说明理由．