第6章 反比例函数复习 北师大版九年级上册教学课件

这是一份第6章 反比例函数复习 北师大版九年级上册教学课件，共25页。

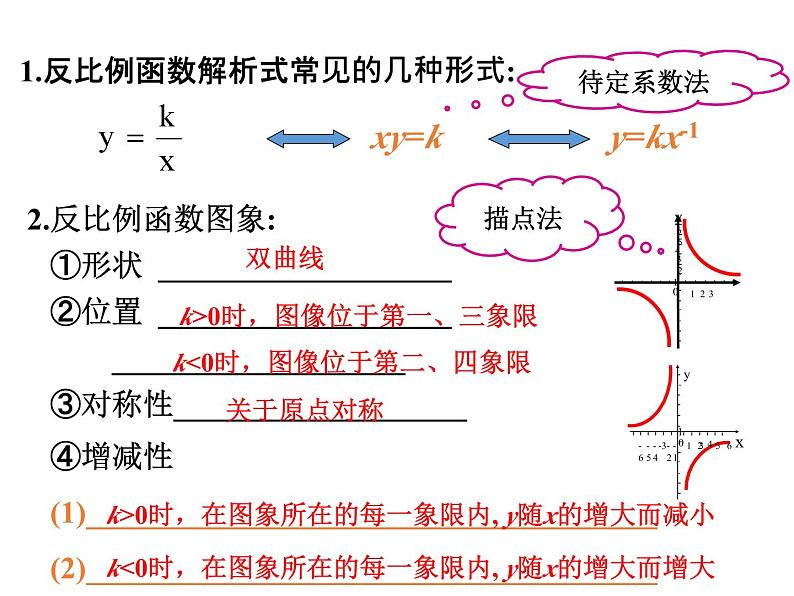
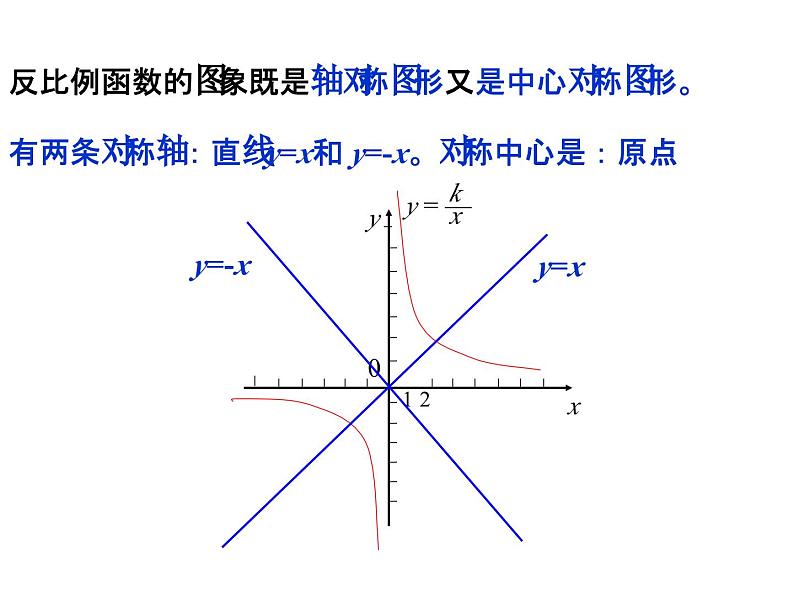
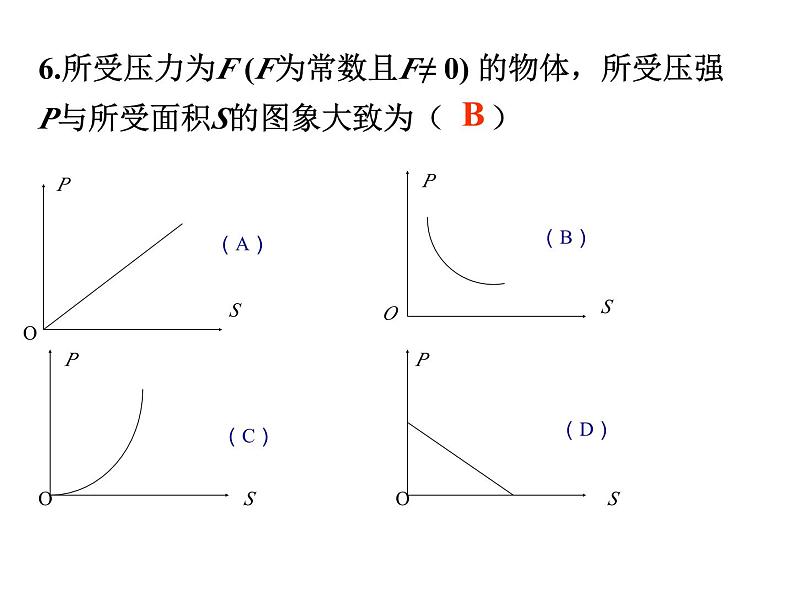
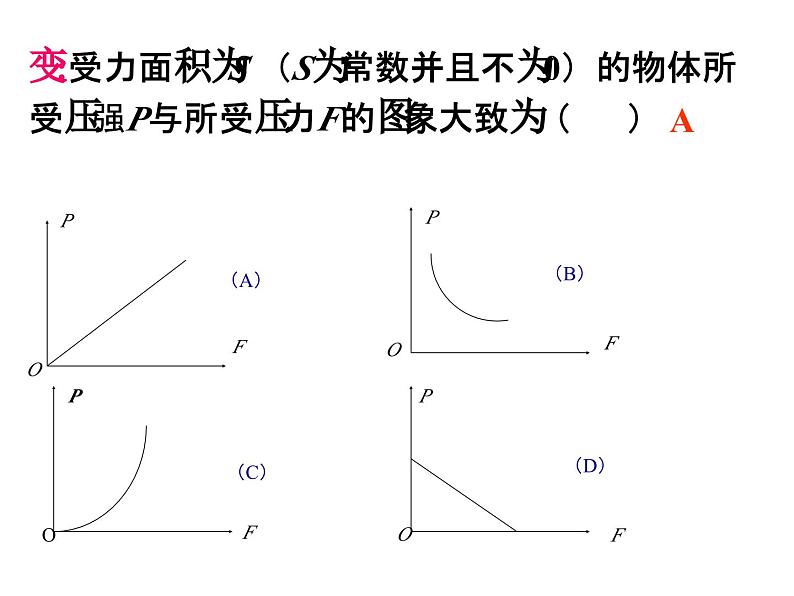
第六章反比例函数复习1.反比例函数解析式常见的几种形式:双曲线k>0时，图像位于第一、三象限k<0时，在图象所在的每一象限内, y随x的增大而增大k<0时，图像位于第二、四象限k>0时，在图象所在的每一象限内, y随x的增大而减小关于原点对称y=kx-1xy=k待定系数法描点法1,4,6比例系数 k分别是3， ，1.判断下列函数是不是反比例函数,并说出比例系数 k:2.已知， . 是反比例函数，则m ，此函数图象在第 象限。3.已知点（1，-2）在反比例函数的图象上，则k= .=3二，四-24.反比例函数的图象大致是（ ）D由1－4m＜0 得－4m＜－ 1 反比例函数的图象既是轴对称图形又是中心对称图形。有两条对称轴：直线y=x和 y=-x。对称中心是：原点xy0126.所受压力为F (F为常数且F≠ 0) 的物体，所受压强P与所受面积S的图象大致为（ ）PPPPSSSSOOOO（A）（B）（C）（D）BPPPPFFFFOOOO（A）（B）（C）（D）变:受力面积为S （S为常数并且不为0）的物体所受压强P与所受压力F的图象大致为（ ）A7.函数y=kx+k与y= (k≠0)在同一坐标中的大致图象为( )ABCDD面积性质（一）面积性质（二）面积性质（三）若将此题改为过P点作y轴的垂线段,其结论成立吗?以上几点揭示了双曲线上的点构成的几何图形的一类性质.掌握好这些性质,对解题十分有益.(上面图仅以P点在第一象限为例). 1:如图,A、B是函数y= 的图象上关于原点对称 的任意两点，AC∥y轴，BC∥x轴，则△ABC的面积S为（ ）A）1 B）2C）S>2 D)10)3:如图，A、C是函数 的图象上关于原点O对称的任意两点，过C向x 轴引垂线，垂足为B，则三角形ABC的面积为 2 4.如图、一次函数 y1= x-2 的图象和反比例 函数 的图象交于A(3,1)、B(n,-3)两点.(1)求k、n的值。(2)x取何值时,y1﹥y2 。AB(1)k=3, n= -1, (2)当x﹥3 或 -1﹤x﹤0时, y1﹥y2 。 1C5.四边形ABCD的面积=_____2ACOxy解：当x=0时, y=2. 即 C (0 ,2） 当y=0时, x=2. 即 A (2 ,0) ∴S⊿AOC =2∴S四边形DCOE =4-2=2∴k=-2 在直角坐标平面内，函数 （x>0，m是常数）的图象经过A(1,4)，B(a，b),其中a>1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，连结AD，DC，CB．（1）若⊿ABD的面积为4，求点B的坐标；（2）求直线AB的函数解析式．x7.A(x1,y1),B(x2,y2)且x1＜0＜x2y1 ＞0＞y2 为了预防“流感”,某学校对教室采用药熏消毒法进行毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x 的函数关系式为: ________, 自变量x 的取值范围是:__________,药物燃烧后y关于x的函数关系式为_____________. 为了预防“流感”,某学校对教室采用药熏消毒法进行毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6 mg,请根据题中所提供的信息,解答下列问题: (2)研究表明,当空气中每立方米的含药量不低 于3 mg且持续时间不低于10 min时,才能有效杀 灭空气中的病菌,那么此次消毒是否有效?为什么?1.先求出教室中含氧量为3mg时的时间点2.再从图像中发现，当消毒过程处于这两个时间点之间时，教室中的含药量是大于等于3 mg。3.将两个时间点相减后与10比较，发现本次消毒是有效的。做题时要注意数形结合2.在一次函数、反比例函数的图象组合图形的面 积计算要注意选择恰当的分解方法.值要注意图象的象限、k值的符号。 3.在函数图形中的面积计算中，要充分利用好横、 纵坐标.4.各种数学思想理解：归类思想、探究思想、转化思想、数形结合思想…….5.根据面积求k 1.S△AOF= 通过本堂课的学习，你有什么收获吗？