初中北师大版3 确定二次函数的表达式教学课件ppt

这是一份初中北师大版3 确定二次函数的表达式教学课件ppt，文件包含北师大版初中数学九年级下册232确定二次函数的表达式第2课时同步课件pptx、北师大版初中数学九年级下册232确定二次函数的表达式第2课时教学设计含教学反思docx等2份课件配套教学资源，其中PPT共18页， 欢迎下载使用。

1.已知三个点坐标时，会用待定系数法，确定二次函数的表达式，体会确定二次函数表达式所需要的条件.
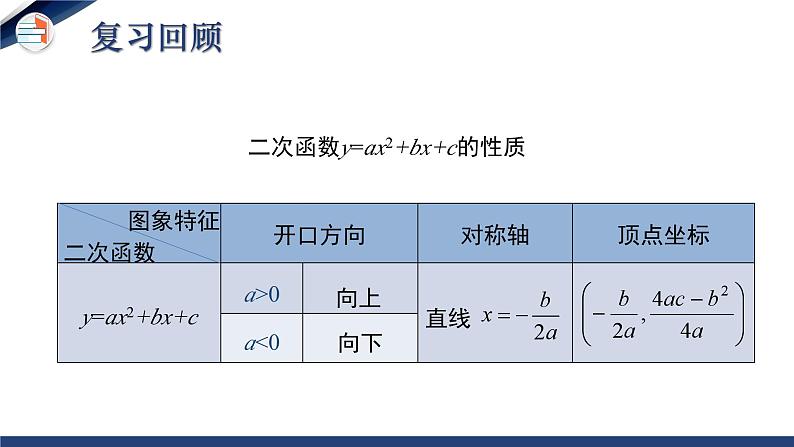
二次函数y=ax2+bx+c的性质
一般式法求二次函数的表达式
（1）二次函数y=ax2+bx+c(a≠0)中有几个待定系数？需要几个抛物线上的点的坐标才能求出来？
（2）下面是我们用描点法画二次函数的图象所列表格的一部分：
解： 设这个二次函数的表达式是y=ax2+bx+c,把（-3，0），（-1，0），（0，-3）代入y=ax2+bx+c得
①选取（-3，0），（-1，0），（0，-3），试求出这个二次函数的表达式.
∴所求的二次函数的表达式是y=-x2-4x-3.
例1:已知二次函数的图象经过(-1,10)，(1,4)，(2,7)三点，求这个二次函数的表达式，并写出它的对称轴和顶点坐标.
因为 ，所以对称轴为直线 ，顶点坐标为 .
例2：已知二次函数的图象经过点A(0,1)，B(1,2)，C(2,1)三点，你能确定这个二次函数的表达式吗？你有几种方法？
这种已知三点求二次函数表达式的方法叫做一般式法.其步骤是：①设函数表达式为y=ax2+bx+c；②代入后得到一个三元一次方程组；③解方程组得到a,b,c的值；④把待定系数用数字换掉，写出函数表达式.
一般式法求二次函数表达式的方法
1.已知抛物线y＝ax2＋bx＋c过（1，－1），（2，－4）和（0，4）三点，那么a，b，c的值分别是（ ） A.a＝－1，b＝－6，c＝4 B.a＝1，b＝－6，c＝－4 C.a＝－1，b＝－6，c＝－4 D.a＝1，b＝－6，c＝4
2.如图，抛物线与x轴交于点（－1，0）和（3，0），与y轴交于点（0，－3），则此抛物线对应的函数的表达式为（ ）A.y＝x2＋2x＋3 B.y＝x2－2x－3C.y＝x2－2x＋3 D.y＝x2＋2x－3
3.已知二次函数y＝ax2＋bx＋c经过点（－1，0），（0，－2），（1，－2），则这个二次函数的表达式为 .4.如图，平面直角坐标系中一条抛物线经过网格点A，B，C，其中B点坐标为（4，4），则该抛物线的表达式为 .
5.已知二次函数的图象经过点(－1，－5)，(0，－4)和(1，1)．求这个二次函数的表达式．
解：设这个二次函数的表达式为y＝ax2＋bx＋c．依题意得
∴这个二次函数的表达式为y＝2x2＋3x－4.
6. 已知，在平面直角坐标系xOy中，抛物线y=ax2+bx+c经过点A（3，0），B（2，-3），C（0，-3）. （1）求抛物线对应的函数表达式；
解：（1）把A（3，0），B（2，-3），C（0,-3）代入y=ax2+bx+c得，9a+3b+c=0，4a+2b+c=-3，c=-3.解得a=1，b=-2，c=-3.所以抛物线的函数表达式为y=x2-2x-3.
（2）设D是抛物线上一点，且点D的横坐标为-2，求△AOD的面积.
②已知顶点坐标或对称轴或最值
③已知抛物线与x轴的两个交点
用一般式法：y=ax2+bx+c
用顶点法：y=a(x－h)2+k
用交点法：y=a(x－x1)(x－x2) (x1, x2为交点的横坐标）
待定系数法求二次函数解析式
1.布置作业：教材 “习题2.7”中第1、2题.2.完成练习册中本课时的练习.