陕西省汉中市南郑区龙岗中学2023-—2024学年上学期九年级期中数学试卷

这是一份陕西省汉中市南郑区龙岗中学2023-—2024学年上学期九年级期中数学试卷，共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（3分）若，则＝（ ）
A．B．C．D．
2．（3分）若方程ax+bx2+c＝0是关于x的一元二次方程，则必须满足的条件是（ ）
A．a≠0B．b≠0
C．c≠0D．以上答案都不正确
3．（3分）如图，若菱形ABCD的对角线AC＝6，BD＝8，连接EF、FG、GH、HE，则四边形EFGH的面积为（ ）
A．10B．11C．12D．24
4．（3分）如图，AD、BC相交于点O，由下列条件不能判定△AOB与△DOC相似的是（ ）
A．AB∥CDB．∠A＝∠DC．D．
5．（3分）一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，在袋中放入3个除了颜色外其余均相同的白球，记录下颜色后，放回袋中并摇匀，摸到白球的频率稳定在0.15附近，则红球的个数为（ ）
A．11B．14C．17D．20
6．（3分）如图，在平行四边形ABCD中，点E在边DC上，连接AE交BD点F，则△DEF的周长与△BAF的周长之比为（ ）
A．9：16B．3：4C．9：1D．3：1
7．（3分）若一元二次方程x2+3x﹣m＝0的两根之和是两根之积的2倍，则m的值为（ ）
A．3B．C．﹣3D．
8．（3分）如图，△ABC和△DEF是以点O为位似中心的位似图形，相似比为2：3（ ）
A．4：9B．9：4C．2：3D．3：2
9．（3分）如图已知线段AB＝2，点C，D是它的黄金分割点（ ）
A．B．C．D．
10．（3分）如图所示，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH，EF＝4，那么线段AD与AB的比等于（ ）
A．25：23B．5：4C．25：24D．4：3
二、填空题（每小题3分，共18分）
11．（3分）若四条线段a、b、c、d是成比例线段，其中a＝3cm，b＝2cm，则d＝ cm．
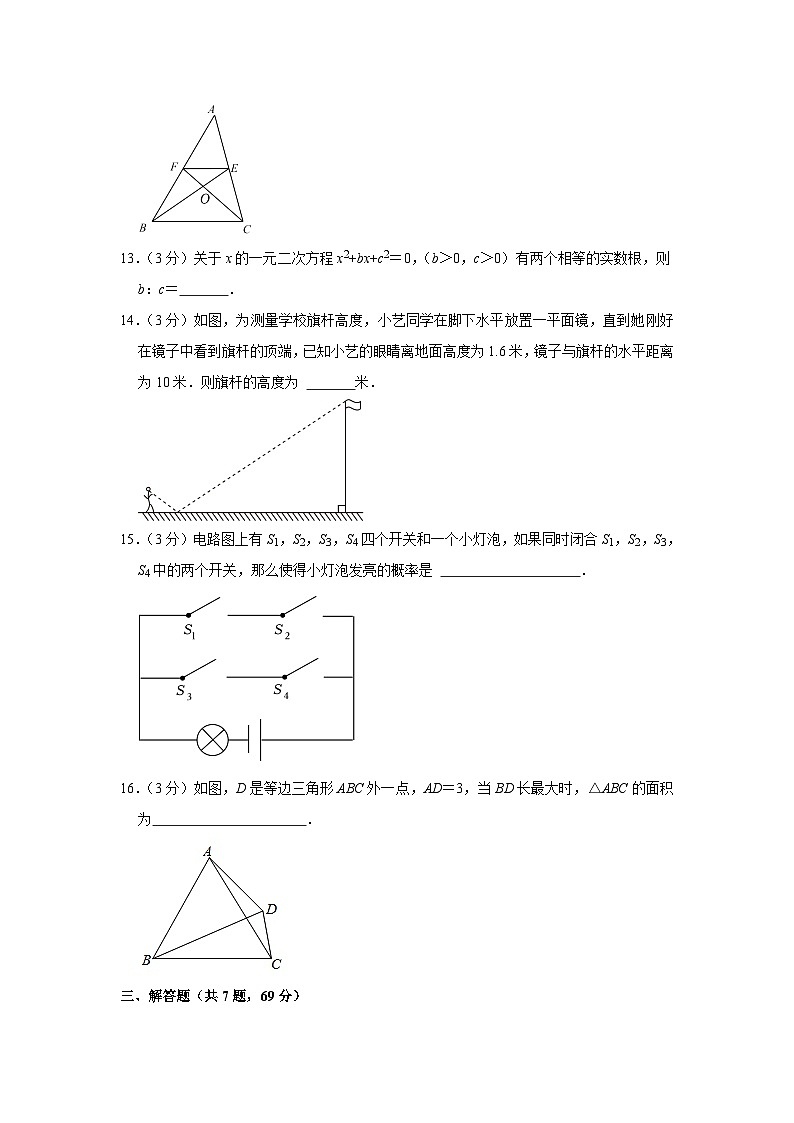
12．（3分）如图，△ABC的中线BE、CF交于点O，连接EF，则 ．
13．（3分）关于x的一元二次方程x2+bx+c2＝0，（b＞0，c＞0）有两个相等的实数根，则b：c＝ ．
14．（3分）如图，为测量学校旗杆高度，小艺同学在脚下水平放置一平面镜，直到她刚好在镜子中看到旗杆的顶端，已知小艺的眼睛离地面高度为1.6米，镜子与旗杆的水平距离为10米．则旗杆的高度为 米．
15．（3分）电路图上有S1，S2，S3，S4四个开关和一个小灯泡，如果同时闭合S1，S2，S3，S4中的两个开关，那么使得小灯泡发亮的概率是 ．
16．（3分）如图，D是等边三角形ABC外一点，AD＝3，当BD长最大时，△ABC的面积为 ．
三、解答题（共7题，69分）
17．（16分）解下列一元二次方程：
（1）（x﹣1）（2x+3）＝0；
（2）；
（3）3x2﹣2x+5＝4；
（4）4（x﹣3）2＝x2．
18．（5分）如图，在△ABC中，AB＝AC，使△ABC∽△DAC．（不写作法，保留作图痕迹）
19．（5分）某班计划选2名学生去参加校外劳动实践，甲、乙、丙、丁4名学生积极报名参加，其中甲是学生会成员
（1）随机抽取1人，甲没被抽中的概率是 ；
（2）若需从这4名学生中随机抽取2人，请用画树状图法或列表法求出被抽到的两名学生都是班级干部的概率．
20．（5分）如图，在菱形ABCD中，点E是边AD上一点，使BF＝AE，连接BE、CF．
求证：BE＝CF．
21．（8分）已知关于x的一元二次方程x2﹣4x﹣m（m+4）＝0．
（1）求证：该无论m取何值，方程总有两个实数根；
（2）若方程的一个根是另一个根的3倍，求m的值．
22．（8分）某市唐朝古塔（图1）所示，我校社会实践小组为了测量塔的高度AB，这时地面上的点E，标杆的顶端点C，测得DE＝3米，将标杆CD沿BD方向平移14米到点H处（DH＝14米），标杆的顶端点C，塔尖点A正好又在同一直线上，点F，H，E，D与塔底处的点B在同一直线上，CD⊥BF，GH⊥BF．请你根据以上数据
24．（12分）（1）如图①，在Rt△ABC中，∠B＝90°，BC＝4．若点P是边AC上一点．则BP的最小值为 ．
（2）如图②，在Rt△ABC中，∠B＝90°，点E是BC的中点．若点P是边AC上一点，求PB+PE的最小值．
（3）公园内有一条四边形ABCD型环湖路，如图③．若AD＝2000米，CD＝1000米，∠B＝90°，∠C＝150°．为满足市民健身需求，EF，FC连接而成的步行景观道，AD上．为了节省成本，要使所修的这条步行景观道最短，求此时BE，DF的长．（路面宽度忽略不计）
2023-2024学年陕西省汉中市南郑区龙岗中学九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（每小题3分，共30分）
1．（3分）若，则＝（ ）
A．B．C．D．
【分析】根据比例的性质得a＝b，再代入所求的式子计算即可．
【解答】解：∵，
∴a＝b，
∴＝＝．
故选：D．
【点评】本题考查了比例的性质，熟练掌握比例的性质是关键．
2．（3分）若方程ax+bx2+c＝0是关于x的一元二次方程，则必须满足的条件是（ ）
A．a≠0B．b≠0
C．c≠0D．以上答案都不正确
【分析】形如ax2+bx+c＝0（a≠0）的方程即为关于x的一元二次方程，据此即可求得答案．
【解答】解：∵方程ax+bx2+c＝0是关于x的一元二次方程，
∴b≠4，
故选：B．
【点评】本题考查一元二次方程，熟练掌握其定义是解题的关键．
3．（3分）如图，若菱形ABCD的对角线AC＝6，BD＝8，连接EF、FG、GH、HE，则四边形EFGH的面积为（ ）
A．10B．11C．12D．24
【分析】连接AC、BD交于O，根据三角形中位线性质得到EH∥BD，FG∥BD，EF∥AC，HG∥AC，推出四边形EFGH是平行四边形，求得∠HEF＝90°，得到四边形EFGH是矩形，解直角三角形得到AC＝AB＝6，BD＝6，于是得到结论．
【解答】解：设AC、BD交于O，
∵四边形ABCD是菱形，
∴AC⊥BD，
∵点E、F、G、H分别是边AB、CD和DA的中点，
∴EH∥BD，FG∥BD，HG∥AC，
∴EH∥FG，EF∥HG，
∴四边形EFGH是平行四边形，
∵AC⊥BD，
∴∠AOB＝90°，
∴∠BAO+∠ABO＝90°，
∵∠AEH＝∠ABO，∠BEF＝∠EAO，
∴∠AEO+∠BEF＝90°，
∴∠HEF＝90°，
∴四边形EFGH是矩形，
∵AC＝6，BD＝8，
∴EH＝＝5＝3，
∴四边形EFGH的面积为3×7＝12，
故选：C．
【点评】本题考查的是中点四边形，掌握菱形的性质、三角形中位线定理是解题的关键．
4．（3分）如图，AD、BC相交于点O，由下列条件不能判定△AOB与△DOC相似的是（ ）
A．AB∥CDB．∠A＝∠DC．D．
【分析】本题中已知∠AOB＝∠DOC是对顶角，应用两三角形相似的判定定理，即可作出判断．
【解答】解：A、由AB∥CD能判定△AOB∽△DOC．
B、由∠AOB＝∠DOC，故本选项不符合题意．
C、由、∠AOB＝∠DOC能判定△AOB∽△DOC．
D、已知两组对应边的比相等：，不能判定△AOB与△DOC相似．
故选：D．
【点评】此题考查了相似三角形的判定：①有两个对应角相等的三角形相似；②有两个对应边的比相等，且其夹角相等，则两个三角形相似；③三组对应边的比相等，则两个三角形相似．
5．（3分）一个不透明的袋中装有若干个红球，为了估计袋中红球的个数，在袋中放入3个除了颜色外其余均相同的白球，记录下颜色后，放回袋中并摇匀，摸到白球的频率稳定在0.15附近，则红球的个数为（ ）
A．11B．14C．17D．20
【分析】根据口袋中有3个白球，利用小球在总数中所占比例得出与实验比例应该相等求出即可．
【解答】解：设红球的个数为x个，根据题意得：
∴＝5.15，
解得：x＝17，
经检验x＝17是原方程的解，
则红球的个数为17个．
故选：C．
【点评】此题主要考查了用样本估计总体，根据已知得出小球在总数中所占比例得出与实验比例应该相等是解决问题的关键．
6．（3分）如图，在平行四边形ABCD中，点E在边DC上，连接AE交BD点F，则△DEF的周长与△BAF的周长之比为（ ）
A．9：16B．3：4C．9：1D．3：1
【分析】由平行四边形的性质推出AB＝DC，DE∥AB，由DE：EC＝3：1，得到DE：DC＝3：4，因此DE：AB＝3：4，由DE∥AB，推出△DEF∽△BAF，得到△DEF的周长与△BAF的周长之比＝DE：AB＝3：4．
【解答】解：∵四边形ABCD是平行四边形，
∴AB＝DC，DE∥AB，
∵DE：EC＝3：1，
∴DE：DC＝8：4，
∴DE：AB＝3：6，
∵DE∥AB，
∴△DEF∽△BAF，
∴△DEF的周长与△BAF的周长之比＝DE：AB＝3：4．
故选：B．
【点评】本题考查相似三角形的判定和性质，平行四边形的性质，关键是由△DEF∽△BAF，得到△DEF的周长与△BAF的周长之比＝DE：AB＝3：4．
7．（3分）若一元二次方程x2+3x﹣m＝0的两根之和是两根之积的2倍，则m的值为（ ）
A．3B．C．﹣3D．
【分析】先设一元二次方程x2+3x﹣m＝0的两根为x1，x2，根据一元二次方程根与系数的关系，求出两根之和与两根之积，由两根之和是两根之积的2倍，列出关于m的方程，求出m即可．
【解答】解：设一元二次方程x2+3x﹣m＝8的两根为x1，x2，
∴x8+x2＝﹣3，x3•x2＝﹣m，
∵一元二次方程x2+6x﹣m＝0的两根之和是两根之积的2倍，
∴﹣4m＝﹣3，
∴，
故选：B．
【点评】本题主要考查了一元二次方程根与系数的关系，解题关键是熟练掌握一元二次方程根与系数的关系．
8．（3分）如图，△ABC和△DEF是以点O为位似中心的位似图形，相似比为2：3（ ）
A．4：9B．9：4C．2：3D．3：2
【分析】根据位似图形的概念得到△ABC∽△DEF，再根据相似三角形的面积比等于相似比的平方计算即可．
【解答】解：∵△ABC和△DEF是以点O为位似中心的位似图形，
∴△ABC∽△DEF，
∵△ABC和△DEF的相似比为2：3，
∴△DEF与△ABC和的相似比为7：2，
∴△DEF和△ABC的面积比为9：5，
故选：B．
【点评】本题考查的是位似变换、相似三角形的性质，熟记相似三角形的面积比等于相似比的平方是解题的关键．
9．（3分）如图已知线段AB＝2，点C，D是它的黄金分割点（ ）
A．B．C．D．
【分析】根据黄金分割的定义进行计算，即可解答．
【解答】解：∵点C是AB的黄金分割点，AC＞BC，
∴＝，
∴AC＝AB＝，
∵点D是AB的黄金分割点，BD＞AD
∴＝，
∴BD＝AB＝，
∴CD＝AC+BD﹣AB＝﹣1+﹣4，
故选：A．
【点评】本题考查了黄金分割，熟练掌握黄金分割的定义是解题的关键．
10．（3分）如图所示，将矩形ABCD的四个角向内折起，恰好拼成一个既无缝隙又无重叠的四边形EFGH，EF＝4，那么线段AD与AB的比等于（ ）
A．25：23B．5：4C．25：24D．4：3
【分析】设点A的对应点为点K，点C的对应点为点L，由矩形的性质得∠A＝∠B＝∠D＝90°，由折叠得KE＝AE＝BE，∠KEH＝∠AEH＝∠AEK，∠KEF＝∠BEF＝∠BEK，可证明∠HEF＝∠EHG＝90°，由EH＝3，EF＝4，根据勾股定理得FH＝＝5，再由×5EK＝×3×4＝S△EFH，求得EK＝，则AH＝KH＝＝，BF＝KF＝＝，由AE＝BE＝KE＝，求得AB＝，再证明△DGH≌△BEF，则DH＝BF＝，所以AD＝AH+DH＝5，则＝，于是得到问题的答案．
【解答】解：设点A的对应点为点K，点C的对应点为点L，
∵四边形ABCD是矩形，
∴∠A＝∠B＝∠D＝90°，
由折叠得KE＝AE＝BE，∠KEH＝∠AEH＝，∠KEF＝∠BEF＝，
∴∠HEF＝∠KEH+∠KEF＝（∠AEK+∠BEK）＝90°，
同理∠EHG＝90°，
∵EH＝3，EF＝4，
∴FH＝＝＝8，
∵∠EKH＝∠A＝90°，∠EKF＝∠B＝90°，∠GLH＝∠D＝90°，
∴H、K、L、F四点在同一条直线上，
∴EK⊥FH，
∴×8EK＝△EFH，
∴EK＝，
∴AH＝KH＝＝＝，BF＝KF＝＝＝，
∵AE＝BE＝KE＝，
∴AB＝2×＝，
∵DG＝CG＝LG＝CDAB，
∴DG＝BE，
∵∠DGH+∠DHG＝90°，∠BEF+∠AEH＝90°，
∴∠DGH＝∠BEF，
∵∠D＝∠B，
∴△DGH≌△BEF（ASA），
∴DH＝BF＝，
∴AD＝AH+DH＝+＝5，
∴＝＝，
故选：C．
【点评】此题重点考查矩形的性质、轴对称的性质、根据面积等式求线段的长度、勾股定理、等角的余角相等、全等三角形的判定与性质等知识与方法，证∠HEF＝∠EHG＝90°并且求得EK＝是解题的关键．
二、填空题（每小题3分，共18分）
11．（3分）若四条线段a、b、c、d是成比例线段，其中a＝3cm，b＝2cm，则d＝ 6 cm．
【分析】根据成比例线段的定义ad＝cb，将a，b及c的值代入即可求得d．
【解答】解：已知a，b，c，d是成比例线段，
根据比例线段的定义得a：b＝c：d，即ad＝cb，
代入a＝3cm、b＝2cm，
得5d＝2×9，
解得：d＝7（cm）．
故答案为：6．
【点评】本题考查了比例线段，掌握成比例线段的定义是解决问题的关键．
12．（3分）如图，△ABC的中线BE、CF交于点O，连接EF，则 ．
【分析】先根据三角形中位线性质得到EF∥BC，EF＝BC，再根据平行线分线段成比例定理得到＝＝，然后利用比例的性质得到的值．
【解答】解：∵△ABC的中线BE、CF交于点O，
∴EF为△ABC的中位线，
∴EF∥BC，EF＝，
∴＝＝，
∴＝．
故答案为：．
【点评】本题考查了三角形的重心：灵活运用三角形中位线性质和平行线分线段成比例定理是解决问题的关键．
13．（3分）关于x的一元二次方程x2+bx+c2＝0，（b＞0，c＞0）有两个相等的实数根，则b：c＝ 2 ．
【分析】根据关于x的一元二次方程x2+bx+c2＝0有两个相等的实数根，可得b2﹣4c2＝0，又b＞0，c＞0，故b＝2c，即可得到答案．
【解答】解：∵关于x的一元二次方程x2+bx+c2＝5有两个相等的实数根，
∴Δ＝0，
即b2﹣5c2＝0，
∴（b+3c）（b﹣2c）＝0，
∵b＞2，c＞0，
∴b﹣2c＝5，即b＝2c，
∴b：c＝（2c）：c＝2；
故答案为：2．
【点评】本题考查一元二次方程根的判别式，解题的关键是掌握ax2+bx+c＝0（a≠0）有两个相等的实数根，需满足Δ＝0．
14．（3分）如图，为测量学校旗杆高度，小艺同学在脚下水平放置一平面镜，直到她刚好在镜子中看到旗杆的顶端，已知小艺的眼睛离地面高度为1.6米，镜子与旗杆的水平距离为10米．则旗杆的高度为 8 米．
【分析】证明△AOB∽△COD，根据相似三角形的性质得到＝，把已知数据代入计算即可．
【解答】解：由题意得：∠ABO＝∠CDO＝90°，∠AOB＝∠COD，
∴△AOB∽△COD，
∴＝，
∵AB＝1.6米，OB＝7米，
∴＝，
解得：CD＝8，
∴旗杆的高度为8米，
故答案为：6．
【点评】本题考查的是相似三角形的应用，掌握相似三角形的判定定理是解题的关键．
15．（3分）电路图上有S1，S2，S3，S4四个开关和一个小灯泡，如果同时闭合S1，S2，S3，S4中的两个开关，那么使得小灯泡发亮的概率是 ．
【分析】根据列表法求概率即可求解．
【解答】解：列表如下，
共有12种等可能结果，符合题意的有8种，
∴使得小灯泡发亮的概率是，
故答案为：．
【点评】本题考查了列表法求概率，掌握求概率的方法是解题的关键．
16．（3分）如图，D是等边三角形ABC外一点，AD＝3，当BD长最大时，△ABC的面积为 ．
【分析】以CD为边作等边△DCE，连接AE．利用全等三角形的性质证明BD＝AE，利用三角形的三边关系，可得BD的最大值为5，利用直角三角形的性质和勾股定理可求AB2，即可求解．
【解答】解：如图1，以CD为边作等边△DCE．
∵BC＝AC，CD＝CE，
∴∠BCD＝∠ACE，
在△BCD和△ACE中，
，
∴△BCD≌△ACE（SAS），
∴BD＝AE，
在△ADE中，
∵AD＝3，DE＝CD＝8，
∴AE≤AD+DE，
∴AE≤5，
∴AE的最大值为5，
∴BD的最大值为6，
此时点D在AE上，
如图2，过点A作AF⊥BD于F，
∵△BCD≌△ACE，
∴∠BDC＝∠E＝60°，
∴∠ADF＝60°，
∵AF⊥BD，
∴∠DAF＝30°，
∴DF＝AD＝DF＝，
∴BF＝，
∴AB3＝AF2+BF2＝19，
∴△ABC的面积＝AB2＝，
故答案为：．
【点评】本题考查等边三角形的性质，全等三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会添加辅助线，构造全等三角形解决问题，属于中考常考题型．
三、解答题（共7题，69分）
17．（16分）解下列一元二次方程：
（1）（x﹣1）（2x+3）＝0；
（2）；
（3）3x2﹣2x+5＝4；
（4）4（x﹣3）2＝x2．
【分析】（1）根据方程得出两个关于x的一元一次方程，再进一步求解即可；
（2）利用分配方法求解即可；
（3）利用公式法求解即可；
（4）先移项，再利用平方差公式将方程的左边因式分解，继而得出两个关于x的一元一次方程，再进一步求解即可．
【解答】解：（1）（x﹣1）（2x+5）＝0，
∴x﹣1＝8或2x+3＝7，
解得x1＝1，x6＝﹣；
（2）x4﹣2x+8＝0，
x2﹣4x+2＝﹣4+2，
（x﹣）5＝1，
x﹣＝4或x﹣，
解得x1＝+1，x2＝﹣1；
（3）3x2﹣2x+5＝3，
3x2﹣6x+1＝0，
a＝6，b＝﹣2，
∴Δ＝（﹣2）7﹣4×3×5＝﹣8＜0，
∴原方程无解；
（4）∵6（x﹣3）2＝x2，
∴4（x﹣3）8﹣x2＝0，
则（6x﹣6+x）（2x﹣7﹣x）＝0，
∴3x﹣5＝0或x﹣6＝4，
解得x1＝2，x3＝6．
【点评】本题主要考查解一元二次方程，解一元二次方程常用的方法有：直接开平方法、因式分解法、公式法及配方法，解题的关键是根据方程的特点选择简便的方法．
18．（5分）如图，在△ABC中，AB＝AC，使△ABC∽△DAC．（不写作法，保留作图痕迹）
【分析】作线段AC的垂直平分线交BC于点D，连接AD，点D即为所求．
【解答】解：如图，点D即为所求．
理由：由作图可知DA＝DC，
∴∠C＝∠DAC，
∵AB＝AC，
∴∠B＝∠C＝∠DAC，
∴△ABC∽△DAC．
【点评】本题考查作图﹣相似变换，等腰三角形的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
19．（5分）某班计划选2名学生去参加校外劳动实践，甲、乙、丙、丁4名学生积极报名参加，其中甲是学生会成员
（1）随机抽取1人，甲没被抽中的概率是 ；
（2）若需从这4名学生中随机抽取2人，请用画树状图法或列表法求出被抽到的两名学生都是班级干部的概率．
【分析】（1）直接利用概率公式可得答案．
（2）画树状图得出所有等可能的结果数以及被抽到的两名学生都是班级干部的结果数，再利用概率公式可得出答案．
【解答】解：（1）由题意得，随机抽取1人．
故答案为：．
（2）画树状图如下：
共有12种等可能的结果，其中被抽到的两名学生都是班级干部的结果有：（乙，（乙，（丙，（丙，（丁，（丁，共8种结果，
∴被抽到的两名学生都是班级干部的概率为＝．
【点评】本题考查列表法与树状图法、概率公式，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．
20．（5分）如图，在菱形ABCD中，点E是边AD上一点，使BF＝AE，连接BE、CF．
求证：BE＝CF．
【分析】由菱形的性质得出AD∥BC，AB＝BC，得出∠A＝∠CBF，证明△ABE≌△BCF（SAS），即可得出BE＝CF．
【解答】证明：∵四边形ABCD是菱形，
∴AD∥BC，AB＝BC，
∴∠A＝∠CBF，
在△ABE和△BCF中，，
∴△ABE≌△BCF（SAS），
∴BE＝CF．
【点评】本题考查了菱形的性质、平行线的性质、全等三角形的判定与性质；熟练掌握菱形的性质，证明三角形全等是解决问题的关键．
21．（8分）已知关于x的一元二次方程x2﹣4x﹣m（m+4）＝0．
（1）求证：该无论m取何值，方程总有两个实数根；
（2）若方程的一个根是另一个根的3倍，求m的值．
【分析】（1）利用一元二次方程的根的判别式即可求解；
（2）利用根与系数的关系建立关于m的方程即可求解．
【解答】（1）证明：∵关于x的一元二次方程x2﹣4x﹣m（m+3）＝0，
∴Δ＝（﹣4）3﹣4×1×[﹣m（m+5）]
＝4（m2+7m+4）
＝4（m+3）2≥0，
∴该无论m取何值，方程总有两个实数根；
（2）解：∵方程的一个根是另一个根的5倍，
∴设方程的一个根为x，则另一个根为3x，
∴根据韦达定理得：x+3x＝3，
∴x＝1，
∴x•3x＝﹣m（m+5）＝3，
∴m＝﹣1或﹣5．
【点评】此题主要考查了一元二次方程的判别式及根与系数的关系，解题的关键是利用根与系数的关系建立关于m的方程解决问题．
22．（8分）某市唐朝古塔（图1）所示，我校社会实践小组为了测量塔的高度AB，这时地面上的点E，标杆的顶端点C，测得DE＝3米，将标杆CD沿BD方向平移14米到点H处（DH＝14米），标杆的顶端点C，塔尖点A正好又在同一直线上，点F，H，E，D与塔底处的点B在同一直线上，CD⊥BF，GH⊥BF．请你根据以上数据
【分析】根据垂直的定义和相似三角形的判定和性质定理即可得到结论．
【解答】解：∵BA⊥AF，DC⊥AF，
∴∠ABC＝∠CDE＝∠GHF＝90°，
∵∠DEC＝∠BEA，
∴△EDC∽△EBA，
∴＝，
∴＝，
∵∠HFG＝∠BFA，
∴△HFG∽△BFA，
∴＝，
∴＝，
∴＝，
∴BD＝42，
∴＝，
∴AB＝30（米），
答：此塔的高度有30米．
【点评】本题考查了相似三角形的应用，熟练掌握A字模型相似三角形是解题的关键．
24．（12分）（1）如图①，在Rt△ABC中，∠B＝90°，BC＝4．若点P是边AC上一点．则BP的最小值为 ．
（2）如图②，在Rt△ABC中，∠B＝90°，点E是BC的中点．若点P是边AC上一点，求PB+PE的最小值．
（3）公园内有一条四边形ABCD型环湖路，如图③．若AD＝2000米，CD＝1000米，∠B＝90°，∠C＝150°．为满足市民健身需求，EF，FC连接而成的步行景观道，AD上．为了节省成本，要使所修的这条步行景观道最短，求此时BE，DF的长．（路面宽度忽略不计）
【分析】（1）过B作BP⊥AC于P，由垂线段最短可知，BP⊥AC时，BP的值最小，由面积法即可求解；
（2）作E关于直线AC的对称点E'，连接CE'，EE'，BE'，BE'交AC于P，由E，E'关于直线AC对称，可知PB+PE＝PB+PE'，而B，P，E'共线，故此时PB+PE最小，最小值为BE'的长度，根据∠B＝90°，AB＝BC＝2，点E是BC的中点，可得CE＝CE'＝1，∠BCE'＝90°，再用勾股定理可得答案；
（3）作C关于AD的对称点M，连接DM，CM，CM交AD于H，作C关于AB的对称点N，连接BN，延长DC，AB交于G，连接NG，连接MN交AB于E，交AD于F，由C，N关于AB对称，C，M关于AD对称，CE＝NE，CF＝MF，又N，E，F，M共线，知此时CE+EF+CF最小，根据∠A＝60°，∠ABC＝90°，∠BCD＝150°，可得∠ADC＝60°，∠MCD＝∠CMD＝30°，即得DH＝CD＝500米，CH＝MH＝DH＝500米，CM＝1000米，由∠ADC＝60°，∠A＝60°，知△ADG是等边三角形，从而CG＝DG﹣CD＝1000米，同理可得CG＝NG＝1000米，∠BNG＝∠BCG＝30°，即得BG＝CG＝500米，BC＝BN＝BG＝500米，故CN＝1000米＝CM，知∠CNM＝∠CMN＝30°，在Rt△BNE中，BE＝＝＝500米，在Rt△MHF中，FH＝＝＝500米，即得DF＝FH+DH＝1000米．
【解答】解：（1）过B作BP⊥AC于P，如图：
由垂线段最短可知，BP⊥AC时，
∵∠ABC＝90°，AB＝3，
∴AC＝＝5，
∵S△ABC＝AB•BC＝，
∴BP＝＝
故答案为：；
（2）作E关于直线AC的对称点E'，连接CE'，BE'，如图：
∵E，E'关于直线AC对称，
∴PE＝PE'，
∴PB+PE＝PB+PE'，
∵B，P，E'共线，
∴此时PB+PE最小，最小值为BE'的长度，
∵∠B＝90°，AB＝BC＝2，
∴∠ACB＝45°，
∵点E是BC的中点，
∴CE＝2，
∵E，E'关于直线AC对称，
∴∠ACE'＝∠ACB＝45°，CE＝CE'＝1，
∴∠BCE'＝90°，
在Rt△BCE'中，
BE'＝＝＝，
∴PB+PE的最小值为；
（3）作C关于AD的对称点M，连接DM，CM交AD于H，连接BN，AB交于G，连接MN交AB于E，如图：
∵C，N关于AB对称，C，
∴CE＝NE，CF＝MF，
∴CE+EF+CF＝NE+EF+MF，
∵N，E，F，M共线，
∴此时CE+EF+CF最小，
∵∠A＝60°，∠ABC＝90°，
∴∠ADC＝60°，
∵C，M关于AD对称，
∴∠MDH＝∠CDH＝60°，∠CHD＝∠MHD＝90°，
∴∠MCD＝∠CMD＝30°，
∴DH＝CD＝500米DH＝500米，
∴CM＝1000米，
∵∠ADC＝60°，∠A＝60°，
∴△ADG是等边三角形，
∴DG＝AD＝2000米，
∴CG＝DG﹣CD＝1000米，
∵∠BCD＝150°，
∴∠BCG＝30°，
∵C，N关于AB对称，
∴C，B，N共线，∠BNG＝∠BCG＝30°，
∴BG＝CG＝500米BG＝500米，
∴CN＝1000米＝CM，
∴∠CNM＝∠CMN，
∵∠BCD＝150°，∠MCD＝30°，
∴∠NCM＝120°，
∴∠CNM＝∠CMN＝30°，
在Rt△BNE中，
BE＝＝＝500米，
在Rt△MHF中，
FH＝＝＝500米，
∴DF＝FH+DH＝500+500＝1000（米），
答：BE的长为500米，DF的长为1000米．
【点评】本题是四边形综合题，考查了直角三角形性质，勾股定理，解直角三角形，等边三角形的判定和性质，轴对称的性质等，解题的关键是作对称，根据两点之间线段最短解决问题．S1
S2
S6
S4
S1
S7S2
S1S5
S1S4
S3
S2S1
S8S3
S2S3
S3
S3S7
S3S2
S2S4
S4
S8S1
S4S6
S4S3