河南省洛阳市洛龙区地矿双语学校2023—2024学年上学期八年级期中数学试卷

这是一份河南省洛阳市洛龙区地矿双语学校2023—2024学年上学期八年级期中数学试卷，共27页。

A．B．
C．D．
2．（2分）设等腰三角形的一边长为5，另一边长为10，则其周长为（ ）
A．15B．20C．25D．20或25
3．（2分）如图所示，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，则∠C′FB等于（ ）
A．70°B．65°C．50°D．25°
4．（2分）如图，直线a∥b，在Rt△ABC中，若∠1＝58°，∠2＝24°（ ）
A．56°B．34°C．36°D．24°
5．（2分）已知∠AOB＝30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1、O、P2三点所构成的三角形是（ ）
A．直角三角形B．钝角三角形
C．等腰直角三角形D．等边三角形
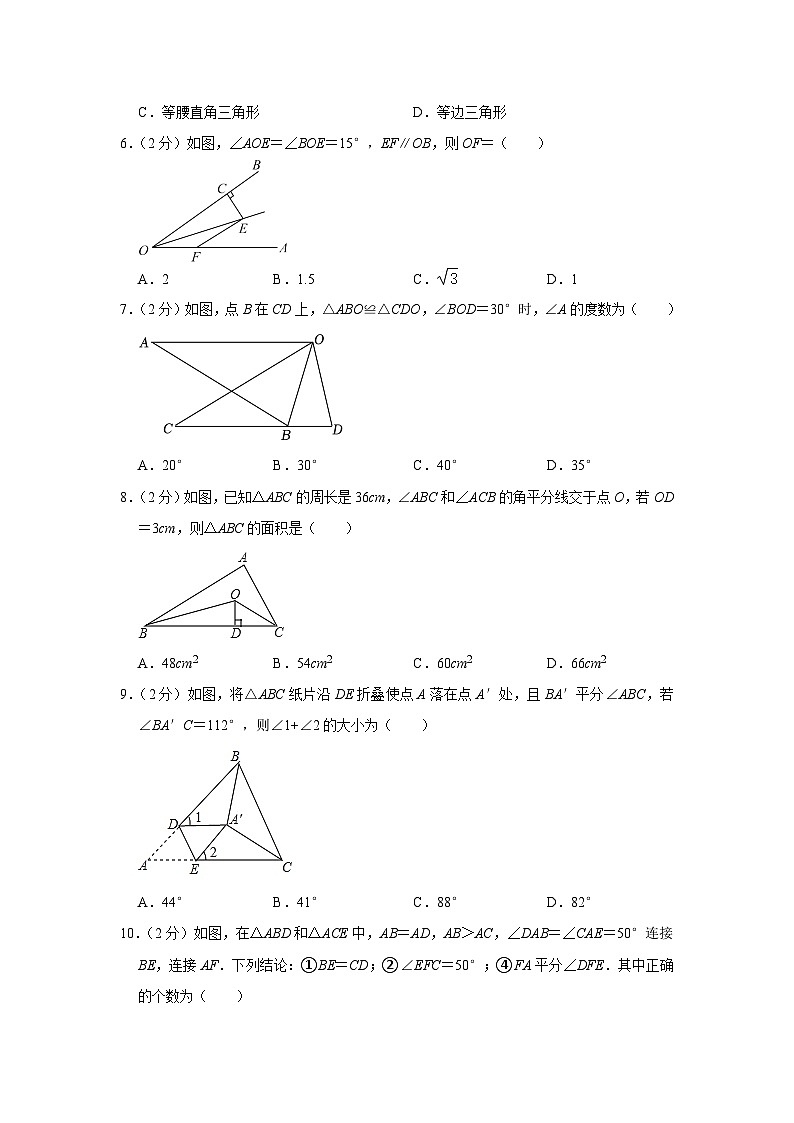
6．（2分）如图，∠AOE＝∠BOE＝15°，EF∥OB，则OF＝（ ）
A．2B．1.5C．D．1
7．（2分）如图，点B在CD上，△ABO≌△CDO，∠BOD＝30°时，∠A的度数为（ ）
A．20°B．30°C．40°D．35°
8．（2分）如图，已知△ABC的周长是36cm，∠ABC和∠ACB的角平分线交于点O，若OD＝3cm，则△ABC的面积是（ ）
A．48cm2B．54cm2C．60cm2D．66cm2
9．（2分）如图，将△ABC纸片沿DE折叠使点A落在点A′处，且BA′平分∠ABC，若∠BA′C＝112°，则∠1+∠2的大小为（ ）
A．44°B．41°C．88°D．82°
10．（2分）如图，在△ABD和△ACE中，AB＝AD，AB＞AC，∠DAB＝∠CAE＝50°连接BE，连接AF．下列结论：①BE＝CD；②∠EFC＝50°；④FA平分∠DFE．其中正确的个数为（ ）
A．1个B．2个C．3个D．4个
二．填空题（共5小题）
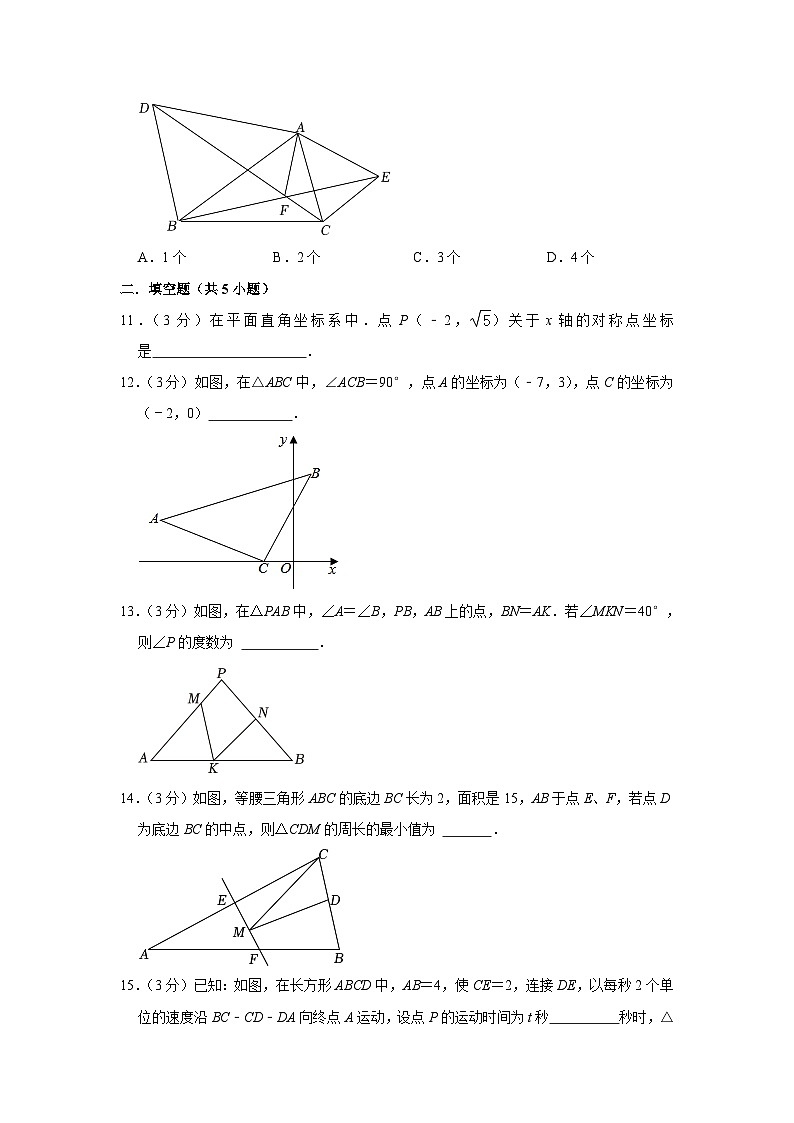
11．（3分）在平面直角坐标系中．点P（﹣2，）关于x轴的对称点坐标是 ．
12．（3分）如图，在△ABC中，∠ACB＝90°，点A的坐标为（﹣7，3），点C的坐标为（﹣2，0） ．
13．（3分）如图，在△PAB中，∠A＝∠B，PB，AB上的点，BN＝AK．若∠MKN＝40°，则∠P的度数为 ．
14．（3分）如图，等腰三角形ABC的底边BC长为2，面积是15，AB于点E、F，若点D为底边BC的中点，则△CDM的周长的最小值为 ．
15．（3分）已知：如图，在长方形ABCD中，AB＝4，使CE＝2，连接DE，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒 秒时，△ABP和△DCE全等．
三．解答题（共8小题）
16．（1）根据图中的相关数据，求出x的值．（3分）
（2）一个多边形的内角和是1260°，求这个多边形的边数．（3分）
17．现要在三角地ABC内建一中心医院，使医院到A、B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置（5分）
18．如图，在四边形ABCD中，AB∥CD，AD＝EC．
（1）求证：△ABD≌△EDC.（3分）
（2）若AB＝1，BE＝3，求CD的长．（3分）
19．如图，在△ABC中，∠CAB＝69°，E分别在边AB，BC上，求∠B的度数．（5分）
20．如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为：A（1，1）（4，2）、C（3，4）．
（1）若△A1B1C1与△ABC关于y轴成轴对称，请在图中作出△A1B1C1，并写出△A1B1C1三个顶点A1，B1，C1的坐标；（6分）
（2）在y轴上一点画出点P，使PA+PB的值最小；（3分）
（3）计算△A1B1C1的面积．（3分）
21．如图，AB＞AC，∠BAC的平分线与BC边的中垂线GD相交于点D，DF⊥AC于点F，求证：BE＝CF．（6分）
22．如图，△ABC是等边三角形，D、E分别是BC、AC边上的点，且AD、BE相交于点P，∠AEB＝∠CDA．
（1）求∠BPD的度数．（5分）
（2）过点B作BQ⊥AD于Q，若PQ＝3，PE＝1，求BE的长. （5分）
23．在通过构造全等三角形解决的问题中，有一种类型的方法是倍延中线．
（1）如图1，AD是△ABC的中线，AB＝7，求AD的取值范围，我们可以延长AD到点M，连接BM，易证△ADC≌△MDB，在△ABM中利用三角形的三边关系可求得AM的取值范围，从而得到中线AD的取值范围是 ；（5分）
（2）如图2，AD是△ABC的中线，点E在边AC上，且AE＝EF，求证：AC＝BF；（5分）
（3）如图3，在四边形ABCD中，AD∥BC，连接CE，ED，试猜想线段BC，CD，并予以证明．（5分）
2023-2024学年河南省洛阳市洛龙区地矿双语学校八年级（上）期中数学试卷
参考答案与试题解析
一．选择题（共10小题）
1．（2分）下列标志中，可以看作是轴对称图形的是（ ）
A．B．
C．D．
【分析】根据轴对称图形的概念，可得答案．
【解答】解：A、是中心对称图形；
B、是中心对称图形；
C、是轴对称图形；
D、是中心对称图形；
故选：C．
【点评】本题考查了轴对称图形，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2．（2分）设等腰三角形的一边长为5，另一边长为10，则其周长为（ ）
A．15B．20C．25D．20或25
【分析】题目给出等腰三角形有两条边长为5和10，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．
【解答】解：分两种情况：
当腰为5时，5+3＝10；
当腰为10时，5+10＞10，周长是：10+10+5＝25．
故选：C．
【点评】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
3．（2分）如图所示，把一个长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，则∠C′FB等于（ ）
A．70°B．65°C．50°D．25°
【分析】根据平角的定义和折叠的性质即可得到结论．
【解答】解：∵∠EFB＝65°，
∴∠EFC＝115°，
∵把一个长方形纸片沿EF折叠后，点D、C′的位置，
∴∠EFC′＝∠EFC＝115°，
∴∠C′FB＝115°﹣65°＝50°，
故选：C．
【点评】本题考查了折叠的性质，平角的定义，熟练掌握折叠的性质是解题的关键．
4．（2分）如图，直线a∥b，在Rt△ABC中，若∠1＝58°，∠2＝24°（ ）
A．56°B．34°C．36°D．24°
【分析】先根据对顶角的定义得出∠3的度数，再由三角形内角与外角的关系求出∠A的度数．
【解答】解：如图，
∵∠1＝58°，a∥b，
∴∠3＝∠8＝58°．
∵∠2＝24°，∠A＝∠3﹣∠5，
∴∠A＝58°﹣24°＝34°．
故选：B．
【点评】本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等是解答此题的关键．
5．（2分）已知∠AOB＝30°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1、O、P2三点所构成的三角形是（ ）
A．直角三角形B．钝角三角形
C．等腰直角三角形D．等边三角形
【分析】由对称性可知OP＝OP1，∠P1OB＝∠BOP，OP＝OP2，∠P2OA＝∠AOP，则有OP1＝OP2，∠P1OP2＝60°，即可求解．
【解答】解：∵P1与P关于OB对称，
∴OP＝OP1，∠P7OB＝∠BOP，
∵P2与P关于OA对称，
∴OP＝OP2，∠P6OA＝∠AOP，
∴OP1＝OP2，∠P7OP2＝2∠BOA，
∵∠AOB＝30°，
∴∠P8OP2＝60°，
∴△P1OP8为等边三角形，
故选：D．
【点评】本题考查轴对称的性质，熟练掌握轴对称的性质，等边三角形的性质是解题的关键．
6．（2分）如图，∠AOE＝∠BOE＝15°，EF∥OB，则OF＝（ ）
A．2B．1.5C．D．1
【分析】过E点作EH⊥OA于H点，如图，根据角平分线的性质得到EH＝EC＝1，再根据平行线的性质得到∠FEO＝∠BOE＝15°，则FE＝FO，接着计算出∠EFH＝30°，则利用含30度角的直角三角形三边的关系得到EF＝2，从而得到OF的长．
【解答】解：过E点作EH⊥OA于H点，如图，
∵∠AOE＝∠BOE＝15°，
∴OE平分∠AOB，
而EC⊥OB，EH⊥OA，
∴EH＝EC＝1，
∵EF∥OB，
∴∠FEO＝∠BOE＝15°，
∴∠FEO＝∠FOE，
∴FE＝FO，
∵∠EFH＝∠FEO+∠FOE＝30°，
∴EF＝2EH＝7，
∴OF＝2．
故选：A．
【点评】本题考查了角平分线的性质：角的平分线上的点到角的两边的距离相等．也考查了平行线的性质、含30度角的直角三角形三边的关系．
7．（2分）如图，点B在CD上，△ABO≌△CDO，∠BOD＝30°时，∠A的度数为（ ）
A．20°B．30°C．40°D．35°
【分析】根据全等三角形对应边相等可得OB＝OD，全等三角形对应角相等可得∠ABO＝∠D，再根据等边对等角求出∠OBD＝∠D，然后求出∠ABC，再根据两直线平行，内错角相等解答即可．
【解答】解：∵△ABO≌△CDO，
∴OB＝OD，∠ABO＝∠D，
∴∠OBD＝∠D＝（180°﹣∠BOD）＝，
∴∠ABC＝180°﹣75°×2＝30°，
∵AO∥BC，
∴∠A＝∠ABC＝30°．
故选：B．
【点评】本题考查了全等三角形的性质，等边对等角的性质，平行线的性质，熟记性质并准确识图是解题的关键．
8．（2分）如图，已知△ABC的周长是36cm，∠ABC和∠ACB的角平分线交于点O，若OD＝3cm，则△ABC的面积是（ ）
A．48cm2B．54cm2C．60cm2D．66cm2
【分析】过点O作OE⊥AC于点E，OF⊥AB于点F，连接OA，根据角平分线的性质可得OD＝OE＝OF＝3cm，再根据S△ABC＝S△AOB+S△BOC+S△AOC＝×OD×C△ABC即可计算结果．
【解答】解：如图，过点O作OE⊥AC于点E，连接OA，
∵OB、OC分别平分∠ABC，OD⊥BC，
∴OD＝OE＝OF＝3（cm），
∴S△ABC＝S△AOB+S△BOC+S△AOC
＝×AB×OF+×AC×OE
＝×OD×C△ABC
＝×2×36
＝54（cm2）．
故选：B．
【点评】本题主要考查角平分线的性质，熟知角平分线的性质是解题关键．
9．（2分）如图，将△ABC纸片沿DE折叠使点A落在点A′处，且BA′平分∠ABC，若∠BA′C＝112°，则∠1+∠2的大小为（ ）
A．44°B．41°C．88°D．82°
【分析】由题意得△ADE≌△A′DE，那么∠DAE＝∠DA′E．如图，连接AA′．根据三角形外角的性质，得∠1＝∠DAA′+∠AA′D，∠2＝∠EAA′+∠AA′E，那么∠1+∠2＝∠DAE+∠DA′E＝2∠DAE．欲求∠1+∠2，需求∠DAE．由三角形内角和定理得∠DAE＝180°﹣∠ABC﹣∠ACB．由BA′平分∠ABC，CA′平分∠ACB，得∠ABC＝2∠A′BC，∠ACB＝2∠A′CB，那么∠ABC+∠ACB＝2∠A′BC+2∠A′CB＝2（∠A′BC+∠A′CB）．由∠BA′C＝112°，得∠A′BC+∠A′CB＝180°﹣∠BA′C＝68°，从而解决此题．
【解答】解：如图，连接AA′．
∵∠BA′C＝112°，
∴∠A′BC+∠A′CB＝180°﹣∠BA′C＝68°．
∵BA′平分∠ABC，CA′平分∠ACB，
∴∠ABC＝2∠A′BC，∠ACB＝2∠A′CB．
∴∠ABC+∠ACB＝7∠A′BC+2∠A′CB＝2（∠A′BC+∠A′CB）＝136°．
∴∠BAC＝180°﹣（∠ABC+∠ACB）＝44°．
由题意得：△ADE≌△A′DE．
∴∠DAE＝∠DA′E＝44°．
∵∠5＝∠DAA′+∠AA′D，∠2＝∠EAA′+∠AA′E，
∴∠1+∠8＝∠DAA′+∠EAA′+∠DA′A+∠EA′A＝∠DAE+∠DA′E＝2∠DAE＝88°．
故选：C．
【点评】本题主要考查三角形内角和定理、角平分线的定义、图形折叠的性质，三角形外角的性质，熟练掌握三角形内角和定理、角平分线的定义、图形折叠的性质，三角形外角的性质是解决本题的关键．
10．（2分）如图，在△ABD和△ACE中，AB＝AD，AB＞AC，∠DAB＝∠CAE＝50°连接BE，连接AF．下列结论：①BE＝CD；②∠EFC＝50°；④FA平分∠DFE．其中正确的个数为（ ）
A．1个B．2个C．3个D．4个
【分析】先由∠DAB＝∠CAE＝50°证明∠BAE＝∠DAC＝50°+∠BAC，即可根据全等三角形的判定定理“SAS”证明△BAE≌△DAC，得BE＝CD，可判断①正确；
设BE交AC于点G，因为∠AEB＝∠ACD，所以∠EFC＝∠CGE﹣∠ACD＝∠CGE﹣∠ABE＝∠CAE＝50°，可判断②正确；
作AI⊥BE于点I，AJ⊥CD于点J，由S△BAE＝S△DAC得AI•BE＝AJ•CD，则AI＝AJ，即可证明FA平分∠DFE，可判断④正确；
假设∠DAF＝∠EAF，则∠DAF﹣∠DAB＝∠EAF﹣∠CAE，所以∠BAF＝∠CAF，由∠AFD＝∠AFE，∠BFD＝∠CFE，得∠AFB＝∠AFC，即可推导出△AFB≌△AFC，得AB＝AC，与已知条件相矛盾，可判断③错误，于是得到问题的答案．
【解答】解：∵∠DAB＝∠CAE＝50°，
∴∠BAE＝∠DAC＝50°+∠BAC，
在△BAE和△DAC中，
，
∴△BAE≌△DAC（SAS），
∴BE＝CD，∠AEB＝∠ACD，
故①正确；
设BE交AC于点G，
∴∠EFC＝∠CGE﹣∠ACD＝∠CGE﹣∠ABE＝∠CAE＝50°，
故②正确；
作AI⊥BE于点I，AJ⊥CD于点J，
∵S△BAE＝S△DAC，
∴AI•BE＝，
∴AI＝AJ，
∴点A在∠DFE的平分线上，
∴FA平分∠DFE，
故④正确；
假设∠DAF＝∠EAF，则∠DAF﹣∠DAB＝∠EAF﹣∠CAE，
∴∠BAF＝∠CAF，
∵∠AFD＝∠AFE，∠BFD＝∠CFE，
∴∠AFD+∠BFD＝∠AFE+∠CFE，
∴∠AFB＝∠AFC，
在△AFB和△AFC中，
，
∴△AFB≌△AFC（ASA），
∴AB＝AC，与已知条件相矛盾，
∴∠DAF≠∠EAF，
故③错误，
∴①②④这3个结论正确，
故选：C．
【点评】此题重点考查全等三角形的判定与性质、根据面积等式证明线段相等、角平分线的判定、三角形的外角等于与它不相邻的两个内角的和等知识与方法，正确地作出所需要的辅助线是解题的关键．
二．填空题（共5小题）
11．（3分）在平面直角坐标系中．点P（﹣2，）关于x轴的对称点坐标是 （﹣2，﹣） ．
【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”解答．
【解答】解：点P（﹣2，）关于x轴的对称点坐标是（﹣6，﹣）．
故答案为：（﹣2，﹣）．
【点评】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：
（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数．
12．（3分）如图，在△ABC中，∠ACB＝90°，点A的坐标为（﹣7，3），点C的坐标为（﹣2，0） （1，5） ．
【分析】先证明△ACD≌△CBE，然后即可得到AD＝CE，DC＝EB，然后再根据点A的坐标为（﹣7，3），点C的坐标为（﹣2，0），即可得到点B的坐标．
【解答】解：作AD⊥x轴于点D，作BE⊥x轴于点E，
则∠ADC＝∠CEB＝90°，
∴∠ACD+∠CAD＝90°，
∴∠ACB＝90°，
∴∠ACD+∠BCE＝90°，
∴∠CAD＝∠BCE，
在△ACD和△CBE中，
，
∴△ACD≌△CBE（AAS），
∴AD＝CE，DC＝EB，
∵点A的坐标为（﹣7，3），3），
∴OD＝7，AD＝3，
∴CE＝3，BE＝OD﹣OC＝7﹣2＝8，
∴OE＝CE﹣OC＝3﹣2＝8，
∴点B的坐标为（1，5），
故答案为：（7，5）．
【点评】本题考查全等三角形的判定与性质、坐标与图形的性质、等腰直角三角形，解答本题的关键是明确题意，利用数形结合的思想解答．
13．（3分）如图，在△PAB中，∠A＝∠B，PB，AB上的点，BN＝AK．若∠MKN＝40°，则∠P的度数为 100° ．
【分析】证明△MAK≌△KBN，根据全等三角形的性质得到∠BKN＝∠AMK，根据三角形的外角性质求出∠A，根据三角形内角和定理计算，得到答案．
【解答】解：在△MAK和△KBN中，
，
∴△MAK≌△KBN（SAS），
∴∠BKN＝∠AMK，
∵∠MKB是△AMK的外角，
∴∠BKN+∠MKN＝∠A+∠AMK，
∴∠A＝∠MKN＝40°，
∴∠B＝∠A＝40°，
∴∠P＝180°﹣40°﹣40°＝100°，
故答案为：100°．
【点评】本题考查的是全等三角形的判定和性质、三角形的外角性质、三角形内角和定理，掌握全等三角形的判定定理是解题的关键．
14．（3分）如图，等腰三角形ABC的底边BC长为2，面积是15，AB于点E、F，若点D为底边BC的中点，则△CDM的周长的最小值为 7 ．
【分析】先根据线段垂直平分线的性质找到最小值，再根据三角形的面积公式求解．
【解答】解：如图，连接AD．
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC＝•BC•AD＝，
∴AD＝6，
∵EF是线段AB的垂直平分线，
∴点C关于直线EF的对称点为点A，
∴AD的长为CM+MD的最小值，
∴△CDM的周长最短为：AD+CD＝8+1＝7，
故答案为：2．
【点评】本题考查了轴对称﹣最短路径问题，理解转化思想是解题的关键．
15．（3分）已知：如图，在长方形ABCD中，AB＝4，使CE＝2，连接DE，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒 1或7 秒时，△ABP和△DCE全等．
【分析】由条件可知BP＝2t，当点P在线段BC上时可知BP＝CE，当点P在线段DA上时，则有AD＝CE，分别可得到关于t的方程，可求得t的值．
【解答】解：
设点P的运动时间为t秒，则BP＝2t，
当点P在线段BC上时，
∵四边形ABCD为长方形，
∴AB＝CD，∠B＝∠DCE＝90°，
此时有△ABP≌△DCE，
∴BP＝CE，即2t＝2；
当点P在线段AD上时，
∵AB＝4，AD＝6，
∴BC＝4，CD＝4，
∴AP＝16﹣2t，
此时有△ABP≌△CDE，
∴AP＝CE，即16﹣6t＝2；
综上可知当t为1秒或4秒时，△ABP和△CDE全等．
故答案为：1或7．
【点评】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法是解题的关键，即SSS、SAS、ASA、AAS和HL．
三．解答题（共8小题）
16．（1）根据图中的相关数据，求出x的值．（3分）
（2）一个多边形的内角和是1260°，求这个多边形的边数．（3分）
【分析】（1）利用多边形的内角和列得方程，解得x的值即可；
（2）设这个多边形的边数为n，利用多边形的内角和列得方程，解得n的值即可．
【解答】解：（1）（x+9）°+115°+90°+x°＝（4﹣2）×180°，
解得：x＝73；
（2）设这个多边形的边数为n，
则（n﹣2）•180°＝1260°，
解得：n＝9，
即这个多边形的边数为3．
【点评】本题考查多边形的内角和，熟练掌握其内角和公式是解题的关键．
17．现要在三角地ABC内建一中心医院，使医院到A、B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置（5分）
【分析】根据线段垂直平分线性质作出AB的垂直平分线，根据角平分线性质作出∠BAC的角平分线，即可得出答案．
【解答】解：
作AB的垂直平分线EF，作∠BAC的角平分线AM，
则P为这个中心医院的位置．
【点评】本题考查了线段垂直平分线性质，角平分线性质的应用，主要考查学生的理解能力和动手操作能力．
18．如图，在四边形ABCD中，AB∥CD，AD＝EC．
（1）求证：△ABD≌△EDC；（3分）
（2）若AB＝1，BE＝3，求CD的长．（3分）
【分析】（1）由“AAS”即可证△ABD≌△EDC；
（2）结合（1）可得AB＝DE，BD＝CD，可得结论．
【解答】（1）证明：∵AB∥CD，
∴∠ABD＝∠EDC．
在△ABD和△EDC中，
，
∴△ABD≌△EDC（AAS），
（2）∵△ABD≌△EDC，
∴AB＝DE＝7，BD＝CD，
∴CD＝BD＝DE+BE＝1+3＝3．
【点评】本题考查了全等三角形的判定和性质，掌握全等三角形的判定方法是本题的关键．
19．如图，在△ABC中，∠CAB＝69°，E分别在边AB，BC上，求∠B的度数．（5分）
【分析】设∠B＝α．根据等腰三角形的性质以及三角形外角的性质得出∠EDB＝∠B＝α，∠CED＝∠EDB+∠B＝2α，∠CDA＝∠DCE+∠B＝3α，然后根据∠CAB＝∠CDA＝69°，即可求解．
【解答】解：设∠B＝α．
∵AC＝DC＝DE＝BE，
∴∠EDB＝∠B＝α，∠CED＝∠ECD，
∴∠CED＝∠EDB+∠B＝2α，∠CDA＝∠DCE+∠B＝3α，
∵∠CAB＝69°，
∴4α＝69°，
∴α＝23°，
即∠B的度数为23°．
【点评】本题考查了等腰三角形的性质以及三角形外角的性质，设∠B＝α，列出关于α的方程是解题的关键．
20．如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为：A（1，1）（4，2）、C（3，4）．
（1）若△A1B1C1与△ABC关于y轴成轴对称，请在图中作出△A1B1C1，并写出△A1B1C1三个顶点A1，B1，C1的坐标；（6分）
（2）在y轴上一点画出点P，使PA+PB的值最小；（3分）
（3）计算△A1B1C1的面积．（3分）
【分析】（1）利用轴对称变换的性质分别作出A，B，C的对应点A1，B1，C1即可；
（2）连接BA′交y轴于点P，连接AP，点P即为所求；
（3）把三角形的面积看成矩形面积减去周围三个三角形面积即可．
【解答】解：（1）如图1，△A1B3C1即为所求．A1（﹣6，1），B1（﹣2，2），C1（﹣4，4）；
（2）如图，点P即为所求；
（3）△A1B2C1的面积为：3×4﹣×5×3﹣×8×2＝3.5．
【点评】本题考查作图﹣轴对称变换，轴对称最短问题等知识，解题的关键是掌握轴对称变换的性质，属于中考常考题型．
21．如图，AB＞AC，∠BAC的平分线与BC边的中垂线GD相交于点D，DF⊥AC于点F，求证：BE＝CF．（6分）
【分析】连接BD，CD，由角平分线的性质和中垂线的性质就可以得出△BED≌△CFD就可以得出结论；
【解答】证明：连接BD，CD．
∵AD平分∠BAC，DE⊥AB，
∴∠AED＝∠BED＝∠AFD＝90°，DE＝DF．
∵DG垂直平分BC，
∴DB＝DC．
在Rt△DEB和Rt△DFC中，
，
∴Rt△DEB≌Rt△DFC（HL），
∴BE＝CF；
【点评】本题考查了角平分线的性质的运用，线段的垂直平分线的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键．
22．如图，△ABC是等边三角形，D、E分别是BC、AC边上的点，且AD、BE相交于点P，∠AEB＝∠CDA．
（1）求∠BPD的度数．（5分）
（2）过点B作BQ⊥AD于Q，若PQ＝3，PE＝1，求BE的长.（5分）
【分析】（1）根据等边三角形的性质可得，∠ABC＝∠C＝60°，又根据∠AEB＝∠CDA，进而求得∠EBC＝∠BAD，即可得出答案；
（2）根据题意求得∠PBQ＝30°，再根据直角三角形中30°的角的性质求出BP的长度，即可得出答案．
【解答】解：（1）由△ABC是等边三角形可得，
∠ABC＝∠C＝60°，
∵∠ADC＝∠ABC+∠BAD，∠AEB＝∠C+∠EBC，
∴∠BAD＝∠EBC，
∵∠BPD＝∠ABE+∠BAD，
∴∠BPD＝∠ABE+∠EBC＝∠ABC＝60°；
（2）∵BQ⊥AD于Q，
∴∠BQP＝90°，
∵∠BPD＝60°，
∴∠PBQ＝90°﹣∠BPD＝30°，
在Rt△BPQ中，
∵PQ＝3，∠PBQ＝30°，
∴BP＝2PQ＝2，
又∵PE＝1，
∴BE＝BP+PE＝6+2＝7．
【点评】此题考查了等边三角形的性质，熟练掌握等边三角形的性质是解题的关键．
23．在通过构造全等三角形解决的问题中，有一种类型的方法是倍延中线．
（1）如图1，AD是△ABC的中线，AB＝7，求AD的取值范围，我们可以延长AD到点M，连接BM，易证△ADC≌△MDB，在△ABM中利用三角形的三边关系可求得AM的取值范围，从而得到中线AD的取值范围是 1＜AD＜6 ；（5分）
（2）如图2，AD是△ABC的中线，点E在边AC上，且AE＝EF，求证：AC＝BF；（5分）
（3）如图3，在四边形ABCD中，AD∥BC，连接CE，ED，试猜想线段BC，CD，并予以证明．（5分）
【分析】（1）如图1中，延长AD到点M，使DM＝AD，连接BM．证明△ADC≌△MDB（SAS），推出AC＝BM＝5，再根据AB﹣BM≤AM≤AB+BM，可得结论；
（2）如图2中，延长AD到T，使得DT＝AD，连接BT．由△ADC≌△TDB，推出AC＝BT，∠C＝∠TBD，推出BT∥AC，再证明BF＝BT，可得结论；
（3）结论：CD＝AD+BC．如图3中，延长CE交DA的延长线于点G．利用全等三角形的性质证明BC＝AG，DC＝DG，可得结论．
【解答】（1）解：如图1中，延长AD到点M，连接BM．
∵AD是△ABC的中线，
∴BD＝CD，
在△ADC和△MDB中，
，
∴△ADC≌△MDB（SAS），
∴AC＝BM＝5，
∵AB＝5，
∴AB﹣BM＜AM＜AB+BM．
∴2＜AM＜12，
∴2＜3AD＜12，
∴1＜AD＜6．
故答案为：7＜AD＜6；
（2）证明：如图2中，延长AD到T，连接BT．
同法可证△ADC≌△TDB，
∴AC＝BT，∠C＝∠TBD，
∴BT∥AC，
∴∠T＝∠DAC，
∵EA＝EF，
∴∠EAF＝∠EFA，
∵∠EFA＝∠BFT，
∴∠T＝∠BFT，
∴BF＝BT，
∴AC＝BF；
（3）解：结论：CD＝AD+BC．
理由：如图8中，延长CE交DA的延长线于点G．
∵AD∥BC，
∴∠G＝∠ECB，
∵E 是AB的中点，
∴AE＝EB，
在△AEG和△BEC中，
，
∴△AEG≌△BEC（AAS），
∴AG＝BC．EC＝EG，
∵DE⊥CG，
∴CD＝GD，
∵DG＝AD+AG＝AD+BC，
∴CD＝AD+BG．
【点评】本题属于四边形综合题，考查了全等三角形的判定和性质，三角形的中线的性质，线段的垂直平分线的性质，等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，倍长中线构造全等三角形解决问题，属于中考压轴题．