2021-2022学年甘肃省天水市第一中学高二下学期学业水平模拟考试（三）数学试题（解析版）

这是一份2021-2022学年甘肃省天水市第一中学高二下学期学业水平模拟考试（三）数学试题（解析版），共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．已知集合，，则（ ）
A．B．
C．D．或
【答案】B
【分析】由交集的定义可求得集合.
【详解】因为，，故.
故选：B.
2．已知直线，，若，则( )
A．B．C．3D．－3
【答案】A
【分析】两直线斜率均存在时，两直线垂直，斜率相乘等于－1，据此即可列式求出a的值．
【详解】∵，∴．
故选：A．
3．已知向量，则（ ）
A．2B．3C．4D．5
【答案】D
【分析】先求得，然后求得.
【详解】因为，所以.
故选：D
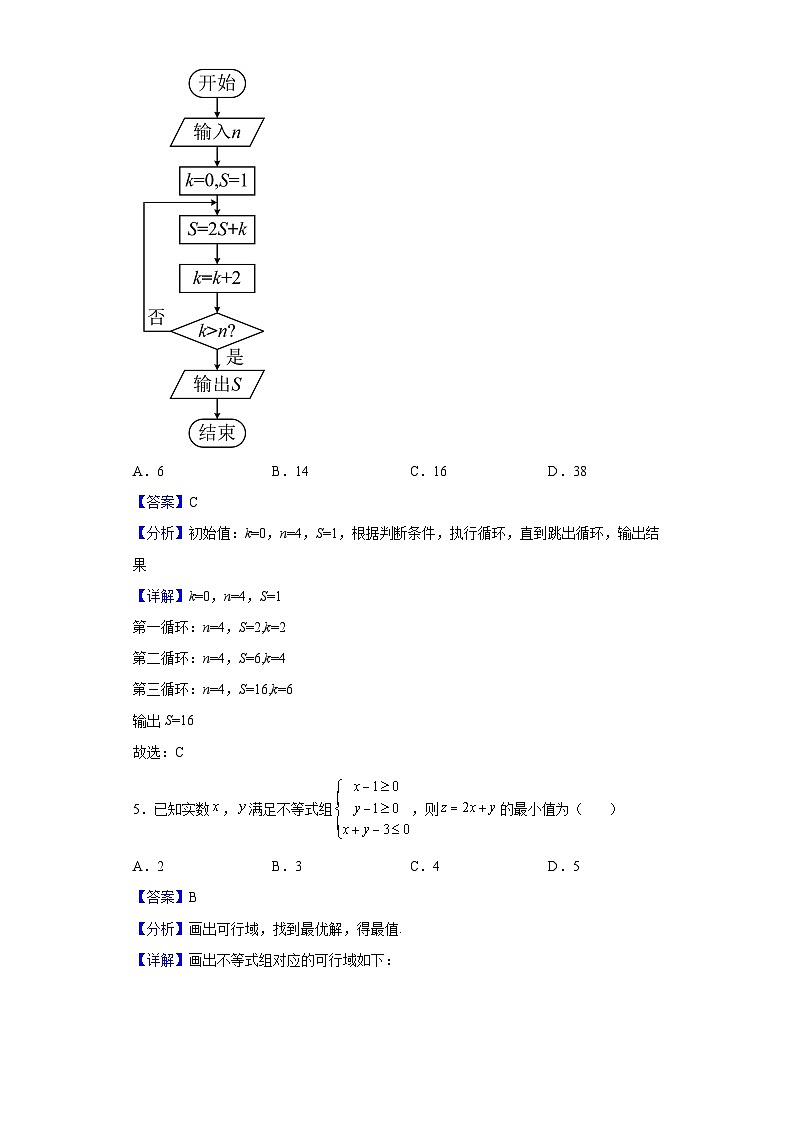
4．如图所示的程序框图，若输入，则输出S的值是（ ）
A．6B．14C．16D．38
【答案】C
【分析】初始值：k=0，n=4，S=1，根据判断条件，执行循环，直到跳出循环，输出结果
【详解】k=0，n=4，S=1
第一循环：n=4，S=2,k=2
第二循环：n=4，S=6,k=4
第三循环：n=4，S=16,k=6
输出S=16
故选：C
5．已知实数，满足不等式组，则的最小值为（ ）
A．2B．3C．4D．5
【答案】B
【分析】画出可行域，找到最优解，得最值.
【详解】画出不等式组对应的可行域如下：
平行移动直线，当直线过点时，
.
故选：B.
6．已知，为了得到的图像，只需将的图像（ ）
A．向左平移个单位B．向左平移个单位
C．向右平移个单位D．向右平移个单位
【答案】A
【分析】根据三角函数平移法则即可得到答案.
【详解】解：因为=，
所以只需给图像向左平移个单位，
即可得到的图像.
故选：A
7．已知圆锥的轴截面是等腰直角三角形，且面积为4，则圆锥的体积为（ ）
A．B．C．D．
【答案】D
【分析】由圆锥轴截面形状和面积易得体高、底面半径均为，利用圆锥体积公式求体积.
【详解】由题设，圆锥的体高、底面半径均为，
所以圆锥的体积为.
故选：D
8．某产品的广告费用x与销售额y的统计数据如下表：
根据收集到的数据（如表），由最小二乘法求得回归方程为.现发现表中有一个数据模糊看不清，则该数据为（ ）A．68B．68.3C．68.5D．70
【答案】A
【分析】先求得的值，再利用回归方程求得的值，进而得到所求数据.
【详解】
又，则
则表中模糊看不清的数据为
故选：A
9．已知，则( )
A．B．C．D．
【答案】A
【分析】根据三角函数诱导公式和余弦二倍角公式即可计算求值．
【详解】．
故选：A．
10．已知点在直线上，则的最小值为（ ）
A．B．C．D．
【答案】A
【分析】由点在直线上，可知，利用基本不等式和“1”的妙用即可求出.
【详解】由点在直线上，可知，
，当且仅当,即，时等号成立.
故选：.
二、填空题
11．已知函数，则___________.
【答案】
【分析】首先求得，可知.
【详解】，.
故答案为：.
12．在中，已知，，，则的面积等于___________.
【答案】
【分析】利用正弦定理可求得，由三角形内角和可得，代入三角形面积公式即可求得结果.
【详解】由正弦定理得：，
又，.
故答案为：.
13．函数的定义域为_______
【答案】
【分析】根据对数型函数的定义域，结合二次根式的性质进行求解即可.
【详解】由题意可知：，
故答案为：.
14．在等比数列中，若，是方程的两根，则_________.
【答案】
【分析】利用韦达定理可得，根据等比数列性质若，则，可得．
【详解】若，是方程的两根，则
∵数列为等比数列，则
故答案为：．
15．直线被圆O；截得的弦长最短，则实数m=___________.
【答案】1
【分析】求出直线MN过定点A（1,1），进而判断点A在圆内，当时，|MN|取最小值，利用两直线斜率之积为-1计算即可.
【详解】直线MN的方程可化为，
由，得，
所以直线MN过定点A（1，1），
因为，即点A在圆内.
当时，|MN|取最小值，
由，得，∴，
故答案为：1.
三、解答题
16．已知函数，求
（1）求函数的最小正周期；
（2）当，求函数的值域．
【答案】（1）；（2）.
【分析】（1）应用二倍角正余弦公式及辅助角公式有，即可求最小正周期；
（2）由题设得，再由正弦函数的性质求值域即可.
【详解】，
（1）最小正周期为；
（2）由知：，故.
17．直三棱柱中，，.
(1)求证：平面.
(2)若与平面所成角为，求三棱锥的体积.
【答案】(1)证明见解析
(2)
【分析】（1）由直棱柱特征和线面垂直性质可得，由和线面垂直判定可得结论；
（2）根据平面可知，由此可求得，利用三棱锥体积公式可求得结果.
【详解】(1)三棱柱为直三棱柱，平面，
又∵平面，，
又∵，即，
又∵，平面，
平面.
(2)三棱柱为直三棱柱，平面，
即为与平面所成角，；
，，，
，
.
18．已知数列是公差为2的等差数列，它的前n项和为Sn，且成等比数列.
（1）求的通项公式；
（2）求数列的前n项和.
【答案】（1），（2）
【分析】（1）由题意可得，从而可求出，进而可求得的通项公式；
（2）由（1）可得，然后利用裂项相消求和法可求得结果
【详解】（1）因为数列是公差为2的等差数列，且成等比数列，
所以即，解得，
所以；
（2）由（1）得，
所以.
19．某省会城市为了积极倡导市民优先乘坐公共交通工具绿色出行，切实改善城市空气质量，缓解城市交通压力，公共交通系统推出“2元换乘畅享公交”“定制公交”“限行日免费乘公交”“绿色出行日免费乘公交”等便民服务措施．为了更好地了解乘坐公共交通的乘客的年龄分布，交管部门对某线路公交车统计整理了某一天1200名乘客的年龄数据，得到的频率分布直方图如下图所示：
(1)求m的值和这1200名乘客年龄的中位数；
(2)现在从年龄分布在人中用分层抽样的方法抽取5人，再从这5人中抽取2人进行问卷调查，求这2人中至少有一人年龄在的概率．
【答案】(1)，中位数为；
(2)
【分析】（1）根据频率分布直方图中所有小矩形的面积之和为得到方程，即可求出，再根据中位数计算公式计算可得；
（2）根据分层抽样求出、的人数，分别记作、、、、，用列举法列出所有可能结果，再根据古典概型的概率公式计算可得；
【详解】(1)解：依题意可得，解得，
因为，所以中位数为于，
设中位数为，则，解得，故这1200名乘客年龄的中位数为；
(2)解：从年龄分布在人中用分层抽样的方法抽取5人，则中抽取人，记作、，
中抽取人，记作、、，
则从这5人中抽取2人进行问卷调查有，，，，，，，，，共个基本事件；
满足这2人中至少有一人年龄在的有，，，，，，共个基本事件，
所以满足这2人中至少有一人年龄在的概率；
20．已知函数.
(1)若函数在是增函数，求的取值范围；
(2)若对于任意的，恒成立，求的取值范围.
【答案】(1)
(2)
【分析】（1）由函数可知对称轴为，由单调性可知，即可求解；
（2）整理问题为在时恒成立，设，则可转化问题为在时恒成立，讨论对称轴与的位置关系，进而求解.
【详解】(1)因为函数，所以对称轴为，
因为在是增函数，所以，解得
(2)因为对于任意的，恒成立，
即在时恒成立，所以在时恒成立，
设，则对称轴为，即在时恒成立，
当，即时，，解得；
当，即时，，解得（舍去），
故.
广告费用x/万元
10
20
30
40
50
销售额y/万元
62
75
81
89