第二章 二次函数（单元小结）（课件+教学设计）-北师大版数学九年级下册

这是一份第二章 二次函数（单元小结）（课件+教学设计）-北师大版数学九年级下册，文件包含北师大版初中数学九年级下册第二章二次函数单元小结同步课件pptx、北师大版初中数学九年级下册第二章二次函数单元小结教学设计含教学反思docx等2份课件配套教学资源，其中PPT共32页， 欢迎下载使用。

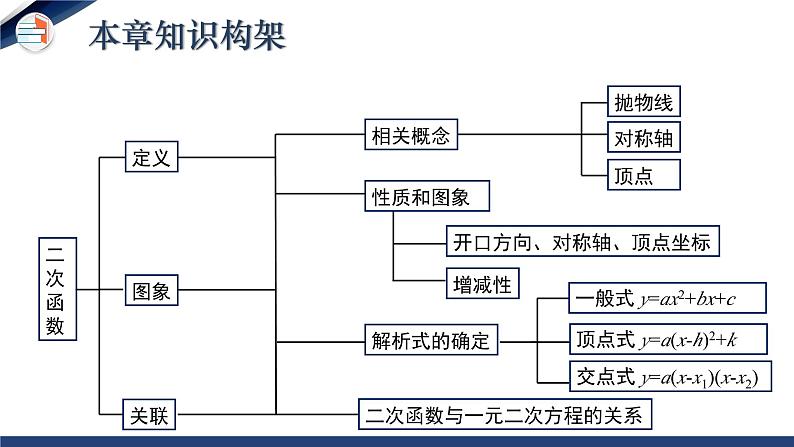
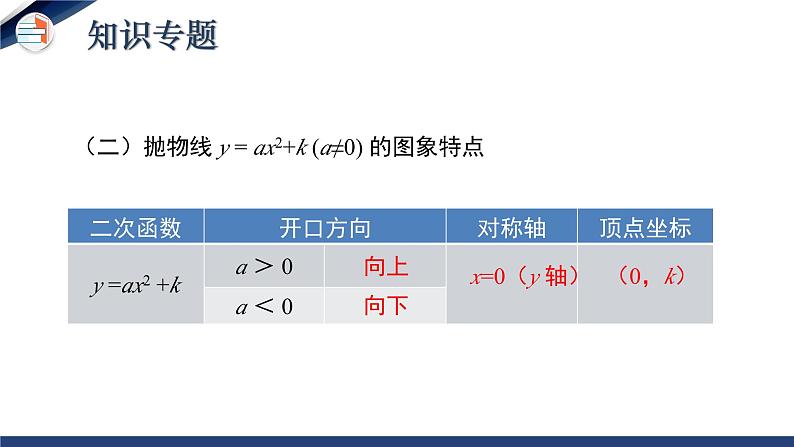
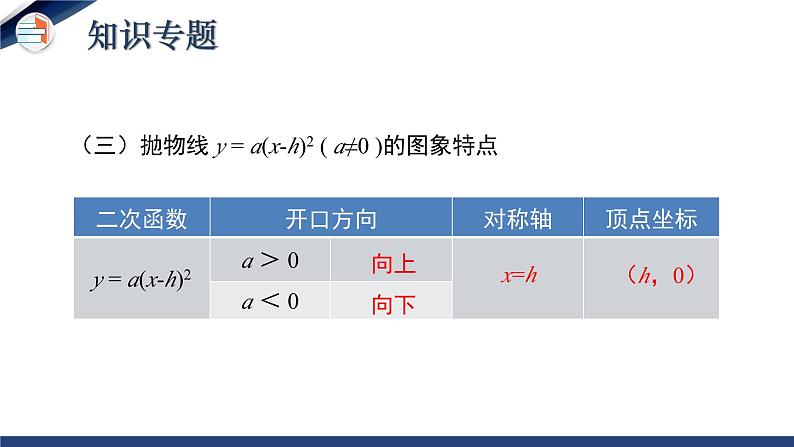
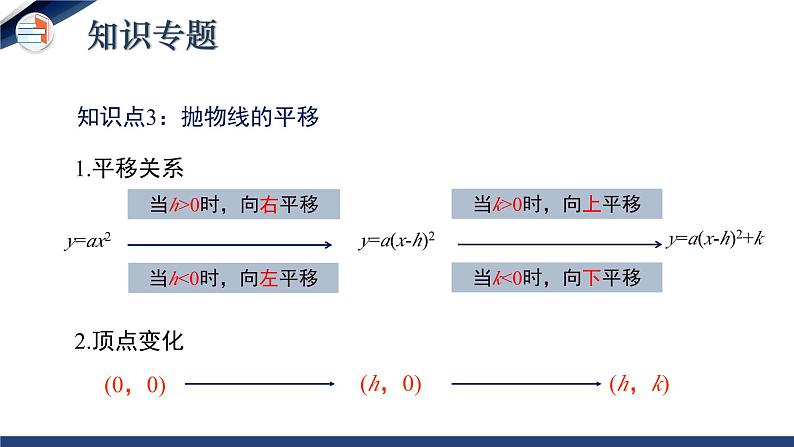
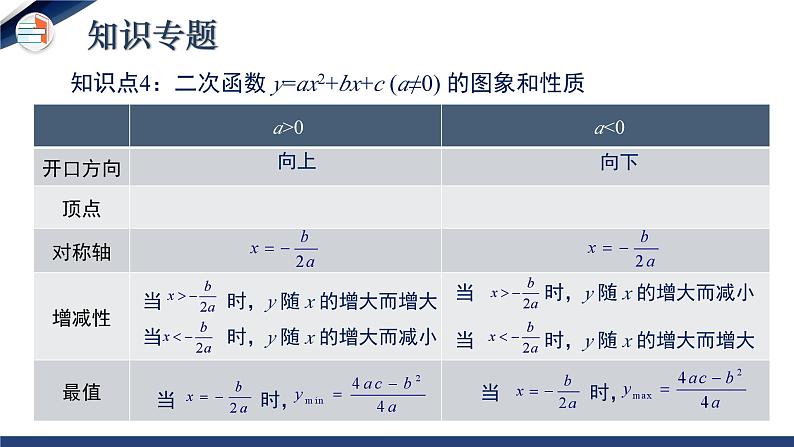
第二章 二次函数 单元小结二次函数定义图象相关概念抛物线对称轴顶点性质和图象开口方向、对称轴、顶点坐标增减性解析式的确定一般式 y=ax2+bx+c顶点式 y=a(x-h)2+k交点式 y=a(x-x1)(x-x2)关联二次函数与一元二次方程的关系本章知识构架知识点1：二次函数的定义定义：一般地，形如 y=ax²+bx+c（a，b，c是常数，a≠ 0）的函数叫做 x 的二次函数.提示：（1）关于 x 的代数式一定是整式，a，b，c 为常数，且a≠0. （2）等式的右边最高次数为 2，可以没有一次项和常数项，但不能没有二次项.知识专题（一）抛物线 y = ax2 (a≠0) 的图象特点 向上向下x=0（y轴）（0，0）知识点2：二次函数的图象与性质知识专题（二）抛物线 y = ax2+k (a≠0) 的图象特点向上向下x=0（y 轴）（0，k）知识专题（三）抛物线 y = a(x-h)2 ( a≠0 )的图象特点 向上向下x=h（h，0）知识专题1.平移关系2.顶点变化当h>0时，向右平移当h<0时，向左平移y=ax2y=a(x-h)2(h，0)(0，0)当k>0时，向上平移 y=a(x-h)2+k(h，k)知识点3：抛物线的平移当k<0时，向下平移知识专题向上向下知识点4：二次函数 y=ax2+bx+c (a≠0) 的图象和性质a>0a<0知识专题二次函数y＝ax2＋bx＋c的图象特征与系数a，b，c的关系知识专题2.已知抛物线顶点坐标（h， k），通常设抛物线解析式为_________________.3.已知抛物线与 x 轴的两个交点(x1，0)， (x2，0)，通常设解析式 为______________________.1.已知抛物线上的三点，通常设解析式为________________.y=ax2+bx+c(a≠0)y=a(x-h)2+k (a≠0)y=a(x-x1)(x-x2) (a≠0)知识点5：二次函数解析式的三种表示方式 知识专题知识点6.二次函数的实际应用最大面积应用题的解题步骤 1.根据要求设出自变量x，因变量y是面积； 2.列出二次函数的解析式，写出自变量取值范围； 3.运用顶点公式或利用配方把解析式化为顶点式求出面积的最大值。知识专题最大利润应用题的解题步骤 1.总利润=单利润×销售数量； 2.设价格为自变量x，总利润为因变量y，列出关系式；3.运用公式法或配方化为顶点式求出利润的最大值.知识专题知识点7.二次函数y=ax2+bx+c与一元二次方程的关系： Δ＞0有两个交点有两个不相等的实根Δ=0有一个交点有两个相等的实根Δ＜0没有交点没有实根与x轴的交点根的情况二次函数y=ax2+bx+c(a≠0)一元二次方程ax2+bx+c=0(a≠0)二次函数y=ax²+bx+c的图象与x轴交点的横坐标就是一元二次方程ax²+bx+c=0的根知识专题专题一 二次函数的图像与性质B考点专练考点专练【要点指导】解决这类问题主要是理解二次函数的定义与性质. 对于二次函数的性质有时要把表达式和图像联系起来理解.考点专练专题二 二次函数y=ax2+bx+c(a≠0)的图像与系数的关系B考点专练考点专练【要点指导】 a的值与图像的开口方向有关, 开口向上时,a＞0；开口向下时, a<0. 当对称轴在y轴左侧时, a, b同号；当对称轴在y轴右侧时, a, b异号．图像与y轴的交点在y轴正半轴上时, c＞0；图像与y轴的交点是原点时, c=0；图像与y轴的交点在y轴负半轴上时, c<0. 当图像与x轴有两个交点时, b2-4ac＞0；当图像与x轴只有一个交点时, b2-4ac=0；当图像与x轴没有交 点时, b2-4ac<0. 考点专练专题三 求二次函数的表达式 例3：已知抛物线y=ax2+bx+c(a≠0)与抛物线y=2x2的开口方向相反、形状相同, 顶点坐标为(3, 5). (1)求抛物线y=ax2+bx+c的函数表达式； (2)求抛物线y=ax2+bx+c与x轴、y轴的交点坐标. 考点专练考点专练【要点指导】 解决这类问题常用待定系数法. 设二次函数表达式时常见的有三种形式：一般式y=ax2+bx+c(a≠0)；顶点式y=a(x-h)2+k(a≠0), 其中(h, k)是二次函数图像的顶点坐标；交点式y=a(x-x1)(x-x2)(a≠0), 其中x1, x2是抛物 线与x轴交点的横坐标.考点专练专题四 二次函数与一元二次方程的关系例4 ：若二次函数y=2(k-1)x2-4kx+2(k-1)的图像与x轴有两个不同的 交点, 求k的取值范围. 考点专练考点专练【要点指导】 二次函数y=ax2+bx+c(a≠0)的图像与x轴的交点有三种情况：没有交点、有一个交点、有两个交点, 这分别对应着一元二次方程 ax2+bx+c=0(a≠0)的根的三种情况：没有实数根、有两个相等的实数根、 有两个不相等的实数根. 考点专练专题五 二次函数的实际应用 例5 ：某公司设计了一款产品, 每件成本是50元, 在试销期间, 据市场调查发现, 当销售单价是60元/件时, 每天的销售量是250件, 而销售单价每增加1元, 每天会少售出5件, 公司决定销售单价x(元/件)不低于60, 而市场要求x不得超过100． (1)求出每天的销售量y(件)与销售单价x(元/件)之间的函数关系式, 并写出x的取值范围； 考点专练(2)求出每天的销售利润W(元)与销售单价x(元/件)之间的函数关系式, 并求出当销售单价为多少时, 每天的销售利润最大, 并求出最大销售利润； (3)若该公司要求每天的销售利润不低于4000元, 但每天的总成本不超过6250元, 则销售单价最低可定为多少？考点专练解: (1)y=250-5(x-60), 即y=-5x+550(60≤x≤100). (2)W=(x-50)(-5x+550), 即W=-5x2+800x-27 500(60≤x≤100). 配方, 得W=-5(x-80)2+4500. ∵a=-5, ∴抛物线开口向下, ∴当x=80时, W有最大值, 为4500, 即当销售单价为80元/件时, 每天的销售利润最大, 最大销售利润为 4500元. 考点专练(3)令W=4000, 则-5(x-80)2+4500=4000, 解得x1=70, x2=90. ∴当W≥4000时, x的取值范围为70≤x≤90. ∵50(-5x+550)≤6250, 解得x≥85, ∴x的取值范围为85≤x≤90, 即销售单价最低可定为85元/件. 考点专练【要点指导】 解决这类问题首先要读懂题意, 找出题目中的变量和不变 量, 构造二次函数解决问题. 这类问题不仅与实际生活有密切联系, 而且还考查我们代数方面和几何方面的综合能力, 常作为压轴题出现. 考点专练1.布置作业：教材“复习题”中第2、3、4、8、13 题2.完成练习册中本课时的练习.　　　作业布置