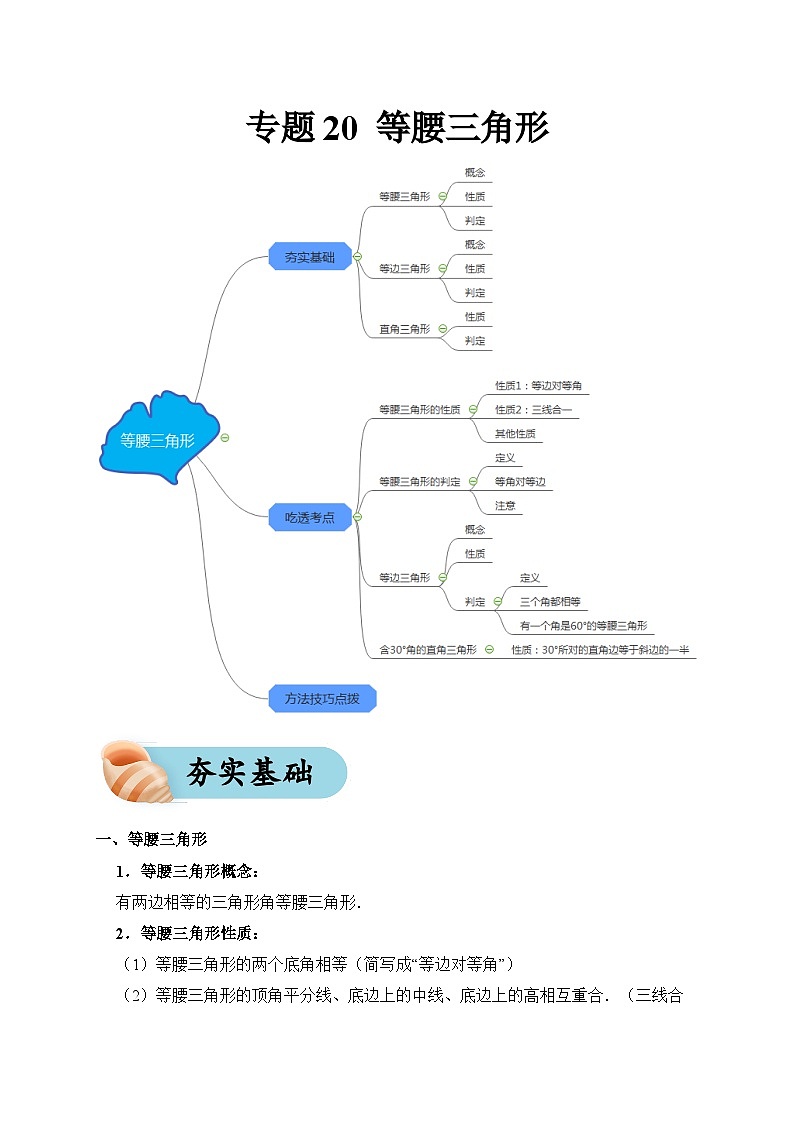
专题20 等腰三角形（夯实基础、考点分析）--2024年中考数学一轮复习（全国通用）

这是一份专题20 等腰三角形（夯实基础、考点分析）--2024年中考数学一轮复习（全国通用），共39页。试卷主要包含了等腰三角形，等边三角形，直角三角形，等边三角形的判定，含30°角的直角三角形的性质等内容，欢迎下载使用。
夯实基础
一、等腰三角形
1．等腰三角形概念：
有两边相等的三角形角等腰三角形．
2．等腰三角形性质：
（1）等腰三角形的两个底角相等（简写成“等边对等角”）
（2）等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．（三线合一）
3．等腰三角形的判定：
如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．
二、等边三角形
1．等边三角形概念
三条边都相等的三角形，叫等边三角形．它是特殊的等腰三角形．
2．等边三角形性质和判定
（1）等边三角形的三个内角都相等，并且每一个角都等于60º．
（2）三个角都相等的三角形是等边三角形．
（3）有一个角是60º的等腰三角形是等边三角形．
三、直角三角形
1．直角三角形性质
（1）直角三角形的两锐角互余；
（2）直角三角形30°角所对的直角边等于斜边的一半；
（3）直角三角形中，斜边上的中线长等于斜边长的一半．
2．直角三角形判定
有一个角是直角的三角形是直角三角形．
3．勾股定理及其逆定理
（1）勾股定理：直角三角形中，两直角边的平方和等于斜边的平方；
（2）勾股定理的逆定理：若一个三角形中有两边的平方和等于第三边的平方，则这个三角形是直角三角形．
吃透考点
一、等腰三角形的性质
性质1：等腰三角形的两个底角相等（简写成“等边对等角”）．
性质2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合（简写成“三线合一”）．
等腰三角形的其他性质：
1．等腰三角形两腰上的中线、高分别相等．
2．等腰三角形两底角的平分线相等．
3．等腰三角形底边上任意一点到两腰的距离之和等于一腰上的高．
4．当等腰三角形的顶角为90°时，此等腰三角形为等腰直角三角形，它的两条直角边相等，两个锐角都是45°．
二、等腰三角形的判定
判定等腰三角形的方法：
1．定义法：有两边相等的三角形是等腰三角形；
2．如果一个三角形有两个角相等，那么这两个角所对的边也相等（简写成“等角对等边”）．
数学语言：在△ABC中，∵∠B=∠C，∴AB=AC（等角对等边）．
【注意】1．“等角对等边”不能叙述为：如果一个三角形有两个底角相等，那么它的两腰也相等．因为在没有判定出它是等腰三角形之前，不能用“底角”“腰”这些名词，只有等腰三角形才有“底角”“腰”．
2．“等角对等边”与“等边对等角”的区别：由两边相等得出它们所对的角相等，是等腰三角形的性质；由三角形有两角相等得出它是等腰三角形，是等腰三角形的判定．
三、等边三角形及其性质
等边三角形的概念：三边都相等的三角形是等边三角形．
等边三角形的性质：等边三角形的三个内角都相等，并且每一个角都等于60°．
四、等边三角形的判定
判定等边三角形的方法：
1．定义法：三边都相等的三角形是等边三角形．
2．三个角都相等的三角形是等边三角形．
3．有一个角是60°的等腰三角形是等边三角形．
五、含30°角的直角三角形的性质
一在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．
【注意】1．该性质是含30°角的特殊直角三角形的性质，一般的直角三角形或非直角三角形没有这个性质，更不能应用．
2．这个性质主要应用于计算或证明线段的倍分关系．
3．该性质的证明出自于等边三角形，所以它与等边三角形联系密切．
4．在有些题目中，若给出的角是15°时，往往运用一个外角等于和它不相邻的两个内角的和将15°的角转化后，再利用这个性质解决问题．
考点1 等腰三角形的性质
【例1】（2023•东方模拟）等腰三角形一腰上的高与另一腰的夹角为，则等腰三角形的底角度数为
A．B．C．或D．或
【答案】
【分析】在等腰中，，为腰上的高，，讨论：当在内部时，如图1，先计算出，再根据等腰三角形的性质和三角形内角和可计算出；当在外部时，如图2，先计算出，再根据等腰三角形的性质和三角形外角性质可计算出．
【解答】解：在等腰中，，为腰上的高，，
当在内部时，如图1，
为高，
，
，
，
；
当在外部时，如图2，
为高，
，
，
，
，
而，
，
综上所述，这个等腰三角形底角的度数为或．
故选：．
【变式练1】（2023•红塔区模拟）已知等腰三角形的周长为20，一边长为4，则这个等腰三角形的底边长为
A．4B．8C．12D．4或12
【答案】
【分析】分两种情况：当腰长为5时，当底边长为5时，分别进行计算即可解答．
【解答】解：分两种情况：
当腰长为4时，等腰三角形的底边长，
，
不能组成三角形，
当底边长为4时，等腰三角形的腰长，
综上所述：此等腰三角形的底边长为4，
故选：．
【变式练2】（2023•雁塔区校级模拟）如图，在中，，于点且，于点，连接，则的长为
A．B．C．5D．6
【答案】
【分析】根据等腰三角形的性质和勾股定理即可得到结论．
【解答】解：，于点且，
，
，
，
故选：．
【变式练3】（2023•泉山区校级三模）已知等腰三角形的两边长分别为4和9，则这个三角形的周长是
A．22B．19C．17D．17或22
【答案】
【分析】分两种情况：①当4为底边长，9为腰长时，即可得出三角形的周长；②当9为底边长，4为腰长时，由，根据三角形的三边关系得出不能构成三角形；即可得出结果．
【解答】解：分两种情况：
①当4为底边长，9为腰长时，，
三角形的周长；
②当9为底边长，4为腰长时，
，
不能构成三角形；
这个三角形的周长是22．
故选：．
【变式练4】（2023•武威一模）一个等腰三角形的顶角是，则它的底角的大小是
A．B．C．D．
【答案】
【分析】等腰三角形中，给出了顶角为，可以结合等腰三角形的性质及三角形的内角和定理直接求出底角，答案可得．
【解答】解：
．
故选：．
【变式练5】（2023•孟村县校级模拟）已知一个等腰三角形的两边长分别是4和8，则该等腰三角形的周长为
A．16或20B．16C．20D．12或24
【答案】
【分析】分腰为4和腰为8两种情况考虑，先根据三角形的三边关系确定三角形是否存在，再根据三角形的周长公式求值即可．
【解答】解：当腰为4时，，
、4、8不能组成三角形；
当腰为8时，，
、8、8能组成三角形，
该三角形的周长为．
故选：．
考点2 等腰三角形的判定
【例2】（2022•仁怀市模拟）将一个三角板和一块直尺如图摆放，要使是等腰三角形，则的度数是
A．B．C．D．
【答案】
【分析】根据等腰三角形的性质求出，再求出，利用平行线的性质可求的度数．
【解答】解：，
，
，
，
，
，
故选：．
【变式练1】（2022•建湖县一模）如图，每个小方格的边长为1，，两点都在小方格的顶点上，点也是图中小方格的顶点，并且是等腰三角形，那么点的个数为
A．1B．2C．3D．4
【答案】
【分析】根据“两圆一线”画图找点即可．
【解答】解：如图，点与、、重合时，均满足是等腰三角形，
故选：．
【变式练2】（2021•雁塔区校级模拟）在中，，，的中垂线交于点，交于点，连接，的角平分线交于点则图中等腰三角形的个数为
A．6B．5C．4D．3
【答案】
【分析】由等腰三角形的判定可得答案．
【解答】解：，，
，是等腰三角形，
是的中垂线，
，是等腰三角形，
，，
，
，
，是等腰三角形，
平分，，
，
和是等腰三角形．
故选：．
【变式练3】（2021•海港区模拟）如图，，，，则图中等腰三角形有 3 个．
【分析】由已知条件，根据三角形内角和等于求得各个角的度数，然后利用等腰三角形的判定进行找寻，注意做到由易到难，不重不漏．
【解答】解：，，，
，
，是等腰三角形，
根据三角形内角和定理知，
，是等腰三角形，
，
，是等腰三角形．
故图中共3个等腰三角形．
故答案为：3．
【变式练4】（2021•广东模拟）如图，在中，、分别是、边上的高，它们相交于点，且．
求证：是等腰三角形．
【答案】证明见解答过程．
【分析】证明即可得出，即可得是等腰三角形．
【解答】证明：、分别是、边上的高，
，，
，，
，
，
在和中，
，
，
，
是等腰三角形．
【变式练5】（2021•永嘉县校级模拟）如图，已知中，是的平分线，又是边上的中线，求证：是等腰三角形．
【分析】作于，于，根据角平分线上的点到角的两边的距离相等可得，再利用“”证明和全等，然后根据全等三角形对应边相等即可证明．
【解答】证明：作于，于，
是的平分线，于，于，
，
是边的中线，
，
在和中，
，
，
．
，
是等腰三角形．
考点3 等腰三角形的判定与性质
【例3】（2023•黑龙江模拟）如图，在中，，，，平分，于点，则的值为
A．24B．12C．6D．3
【答案】
【分析】延长、相交于点，证明，可得，，从而可得，再由，求得，即可求得面积．
【解答】解：延长、相交于点，
平分，，
，，
在和中，
，
，
，，
，
，
，
．
故选：．
【变式练1】（2023•郸城县三模）如图，已知，截线与直线，分别交于点，，以点为圆心，长为半径作弧交直线于点，连接，若，则的度数是
A．B．C．D．
【答案】
【分析】根据题意确定，从而得到，再利用三角形的内角和求解即可．
【解答】解：由题意，，
，
，
，
故选：．
【变式练2】（2023•鼓楼区二模）如图，在中，是上一点，，过点作弦交于，若，则与满足的数量关系是
A．B．C．D．
【答案】
【分析】连接，根据垂直定义可得，从而可得，再根据等腰三角形的性质可得，然后根据已知和等量代换可得，从而可得，再利用三角形是外角性质可得，最后利用等量代换进行计算，即可解答．
【解答】解：连接，
，
，
，
，
，
，，
，
，
是的一个外角，
，
，
，
，
故选：．
【变式练3】（2023•西湖区校级二模）如图，等腰三角形中，，，是的平分线，，则的度数为
A．B．C．D．
【答案】
【分析】根据等腰三角形的性质推出，根据角平分线的定义得出，根据平行线的性质即可得解．
【解答】解：，
，
，
，
是的平分线，
，
，
，
故选：．
【变式练4】（2023•新城区校级模拟）如图，在中，平分，．若，，则的长为
A．13B．12C．10D．9
【答案】
【分析】先根据平行线的性质和角平分线的定义证明，得到，则．
【解答】解：平分，
，
，
，
，
，
，
故选：．
【变式练5】（2023•莱芜区三模）如图，点是的角平分线上一点，点是上一点，且，若，则线段的长是
A．1.8B．2.5C．3D．2
【答案】
【分析】根据角平分线的定义和平行线的性质证得，由等腰三角形的判定即可求出．
【解答】解：点是的角平分线上一点，
，
，
，
，
．
故选：．
考点4 等边三角形的性质
【例4】（2023•渭滨区一模）如图，直线，等边三角形的顶点在直线上，，则的度数为
A．B．C．D．
【答案】
【分析】根据直线，可得，根据等边三角形的性质可得，根据求解即可．
【解答】解：直线，
，
在等边中，，
，
故选：．
【变式练1】（2023•黔东南州二模）如图，在等边三角形中，于点，点是延长线上一点，若，则的度数为
A．B．C．D．
【答案】
【分析】由等边三角形的性质可得，由等腰三角形的性质可求解．
【解答】解：是等边三角形，，
，
，
，
故选：．
【变式练2】（2023•余杭区校级模拟）如图，已知等边，直线，，则
A．B．C．D．
【答案】
【分析】根据等边三角形的性质得出，进而利用平行线的性质和对顶角解答即可．
【解答】解：是等边三角形，
，
直线，，
，
，
，
故选：．
【变式练3】（2023•天长市校级二模）如图，直线，是等边三角形，顶点在直线上，直线交于点，交于点，若，则 的度数是
A．B．C．D．
【答案】
【分析】先根据等边三角形的性质可得，由三角形外角的性质可得的度数，由平行线的性质可得同旁内角互补，可得结论．
【解答】解：是等边三角形，
．
，
，
，
，
，
，
故选：．
【变式练4】（2023•梁溪区一模）如图，在正三角形中，，，，则的面积是
A．B．C．D．
【答案】
【分析】作于，于，交延长线于，设，由勾股定理得到，求出的值，得到的长，由等边三角形的性质求出的长，得到的长，由三角形的面积公式即可求解．
【解答】解：作于，于，交延长线于，
是等边三角形，
，，
，
，
设，
，，
，
，
，
，
，
是等边三角形，，
，
，，，
，
的面积．
故选：．
【变式练5】（2023•淮阳区校级三模）如图，，等边三角形的顶点在直线上，，则的度数为
A．B．C．D．
【答案】
【分析】延长交直线于，根据三角形的一个外角等于与它不相邻的两个内角的和列式求出，再根据两直线平行，内错角相等解答即可．
【解答】解：如图，延长交直线于，
是等边三角形，
，
，
．
故选：．
考点5 等边三角形的判定
【例5】（2022•路北区校级一模）在中，已知，则是
A．等腰三角形B．等边三角形
C．直角三角形D．等腰直角三角形
【答案】
【分析】根据三角形内角和定理求出三个内角的度数即可判断．
【解答】解：设，
，
，
，
，
，
，
该三角形是等腰三角形．
故选：．
【变式练1】（2023•通榆县三模）如图，在中，为延长线上的一点，，．求证：是等边三角形．
【答案】证明过程见解答．
【分析】先利用平角定义求出，再利用三角形内角和定理求出，然后根据等边三角形的判定方法即可解答．
【解答】证明：，
，
，
，
，
是等边三角形．
【变式练2】（2021•南海区一模）如图，已知为的中点，，，点，为垂足，且，，求证：是等边三角形．
【分析】利用“”证明和全等，再根据全等三角形对应角相等可得，然后根据等角对等边得到，再求得，即可解答．
【解答】证明：是的中点，
，
，，
和都是直角三角形，
在和中，
，
，
，
（等角对等边）．
，，
，
是等边三角形．
【变式练3】（2019•玉州区二模）如图，，平分，且，若点，分别在，上，且为等边三角形，则满足上述条件的有
A．2个以上B．2个C．1个D．0个
【答案】
【分析】在和上分别取点、，使得，证明是等边三角形即可得出答案，证明思路可在上取点，使得为等边三角形，再利用证明即可．
【解答】解：如图，在射线上取点，使得，
在射线上取点，使得，
在射线上取点，使得，
平分，
，
，
为等边三角形，
，
，
，
，
为等边三角形．
满足题目条件的有无数个．
故选：．
【变式练4】（2016•门头沟区二模）如图，在中，，，为边上的中线．求证：是等边三角形．
【分析】根据直角三角形的性质得出，即可得出答案．
【解答】证明：，，
，
为边上的中线，
，
，
是等边三角形．
【变式练5】（2012•犍为县模拟）若一个三角形的两个角的平分线分别垂直对边，则这个三角形是
A．等腰三角形B．直角三角形
C．等边三角形D．等腰直角三角形
【分析】已知一个三角形的两个角的平分线分别垂直对边，则可证得角平分线分成的两个三角形全等，即可得三边相等，所以这是一个等边三角形．
【解答】解：已知一个三角形的两个角的平分线分别垂直对边，
则角平分线分成的两个三角形全等，
则这两个角所在的边均相等，
即三边相等，
所以这是一个等边三角形．
故选：．
考点6 等边三角形的判定与性质考点7
【例6】（2023•南山区模拟）如图，等边三角形边长为2，点在边上，且，点在边上且，连接，交于点，在线段上截取，连接，则线段的最小值是 ． ．
【答案】．
【分析】如图所示，连接，取的中点，连接，由全等三鱼形的性质得到，即点为的中点，则，推出点在以为直径的圆上运动，故当、、三点共线时，有最小值，求出，则．
【解答】解：如图所示，连接，取的中点，连接，延长到，使得，则是等边三角形，
，
，
，，
，
，即点为的中点，
是等边三角形，
，即，
点在以为直径的圆上运动，
当、、三点共线时，有最小值，
是等边三角形，是的中点，
，，
，
．
．
故答案为：．
【变式练1】（2023•岳麓区校级模拟）如图，为等边三角形，交于点，交于点．
（1）求证：是等边三角形．
（2）求证：．
【答案】见解答．
【分析】（1）根据等边三角形的性质和平行线的性质证明即可．
（2）根据等边三角形的性质解答即可．
【解答】证明：（1）为等边三角形，
．
，
，．
是等边三角形．
（2）为等边三角形，
．
平分，
．
是等边三角形，
．
．
【变式练2】（2023•张店区校级二模）如图，在等边中，点在边上，过点作交于点，过点作，交的延长线于点．
（1）求的度数；
（2）求证：．
【分析】（1）由平行线的性质求出，再由三角形的内角和定理解决问题即可．
（2）证是等边三角形，得，再证，得，即可得出结论．
【解答】（1）解：是等边三角形，
，
，
，
，
，
；
（2）证明：是等边三角形，
，
，
，
，
是等边三角形，
，
，，
，
，
．
【变式练3】（2022•南谯区校级模拟）已知：如图，和都是等边三角形，是延长线上一点，与相交于点，、相交于点，、相交于点，则下列五个结论：①；②；③；④；⑤是等边三角形．其中，正确的有
A．2个B．3个C．4个D．5个
【分析】根据先证明，得出，根据已知给出的条件即可得出答案；
【解答】解：和都是等边三角形，
，，，
，即，
，
，故选项①正确；
，由得：，
，故选项②正确；
由得：，
是的外角，
，
又是的外角，
，故选项③正确；
在和中，
，
，
，故选项④正确；
，
为等腰三角形，，
是等边三角形，故选项⑤正确；
故选：．
【变式练4】（2022•惠城区一模）将两个直角三角板如图放置，其中，，．如果点是的中点，与交于点，则的度数为 120 ．
【答案】120．
【分析】先根据直角三角形斜边上的中线等于斜边的一半得出，由，得到是等边三角形，那么，，再根据三角形外角的性质可得出答案．
【解答】解；，点是的中点，
，
，
是等边三角形，
，
，
，
，
故答案为：120．
【变式练5】（2021•台安县模拟）如图，在中，为上一点，，且，，则 10 ．
【分析】根据等腰三角形的性质和等边三角形的判定和性质定理即可得到结论．
【解答】解：，
，
，
，
是等边三角形，
，
，
，
故答案为：10．
考点7 含30度角的直角三角形
【例7】（2023•利辛县模拟）如图，在中，，，，点为的中点，点为上一动点，点从点出发运动到点处停止，设点经过的路程为，，令，则的最小值为
A．B．7C．5D．
【答案】
【分析】作于，由直角三角形的性质得到，，得到，由勾股定理得到，因此，即可求出的最小值．
【解答】解：作于，
，，
，，
，
，，
是中点，
，
，
，
，，
，
，
，
，
，
，
的最小值为．
故选：．
【变式练1】（2023•西安二模）如图，在中，，，，点为的中点，于点，则的长是
A．1B．C．3D．6
【答案】
【分析】由直角三角形的性质，得到，由等腰三角形的性质得到，由三角形外角的性质得到，因此是等边三角形，由等腰三角形的性质即可求出的长．
【解答】解：，，点为的中点，
，
，
，
是等边三角形，
于点，
．
故选：．
【变式练2】（2023•香洲区校级一模）如图，三角形中，，是高，，，则的长为
A．1B．2C．2.5D．3
【答案】
【分析】根据含角的直角三角形的性质可得的长，再据含角的直角三角形的性质可得的长．
【解答】解：，，，
，，
，
，
，
，
故选：．
【变式练3】（2023•宝鸡模拟）如图，在中，，，为上一点，，则的长为
A．8B．7C．6D．10
【答案】
【分析】由等腰直角三角形的性质推出，由直角三角形的性质得到．
【解答】解：，
，
，
，
，
，
，
．
故选：．
【变式练4】（2023•高州市校级二模）如图，在中，，，，则的长是
A．8B．1C．12D．4
【答案】
【分析】根据含30度角的直角三角形的性质即可求解．
【解答】解：在中，
，，，
的长是12．
故选：．
【变式练5】（2023•大同模拟）将三角尺按如图所示的方式放置在一张矩形纸片上，，，，则的度数为
A．B．C．D．
【答案】
【分析】由锐角的正弦定义求出，由对顶角的性质得到，由三角形内角和定理求出的度数，即可得到的度数．
【解答】解：交于，交于，
，，
，
，
，
，
．
故选：．
方
法
技
巧
点
拨
1．等腰三角形
（1）应用“三线合一”性质的前提条件是在等腰三角形中，且必须是底边上的中线、底边上的高和顶角平分线，若是一腰上的高与中线就不一定重合．
（2）等腰三角形是轴对称图形，顶角平分线（或底边上的高、底边上的中线）所在的直线是它的对称轴．
2．等边三角形
（1）判定等边三角形时常用的选择方法：
若已知三边关系，一般选用：三边都相等的三角形是等边三角形；
若已知三角关系，一般选用：三个角都相等的三角形是等边三角形；
若已知该三角形是等腰三角形，一般选用：有一个角是60°的等腰三角形是等边三角形．
（2）等边三角形是特殊的等腰三角形，它具有等腰三角形的一切性质．
3．含30°角的直角三角形
（1）在直角三角形中，30°角所对的直角边等于斜边的一半．
（2）含30°角的直角三角形的性质是求线段长度和证明线段倍分关系的重要依据．