山东省潍坊市寿光市、昌邑市2023—2024学年上学期九年级期中数学试卷

这是一份山东省潍坊市寿光市、昌邑市2023—2024学年上学期九年级期中数学试卷，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．（4分）若锐角A满足csA＝，则∠A的度数是（ ）
A．30°B．45°C．60°D．75°
2．（4分）方程（x+1）2＝4的解为（ ）
A．x1＝1，x2＝﹣3B．x1＝﹣1，x2＝3
C．x1＝2，x2＝﹣2D．x1＝1，x2＝﹣1
3．（4分）用配方法解方程x2+4x+1＝0时，配方结果正确的是（ ）
A．（x﹣2）2＝5B．（x﹣2）2＝3C．（x+2）2＝5D．（x+2）2＝3
4．（4分）如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC＝25°，OC的延长线交PA于点P，则∠P的度数是（ ）
A．25°B．35°C．40°D．50°
5．（4分）已知点A（a，b）在第四象限，则关于x的一元二次方程ax2+2x+b＝0的根的情况是（ ）
A．没有实数根
B．有两个相等的实数根
C．有两个不相等的实数根
D．无法确定
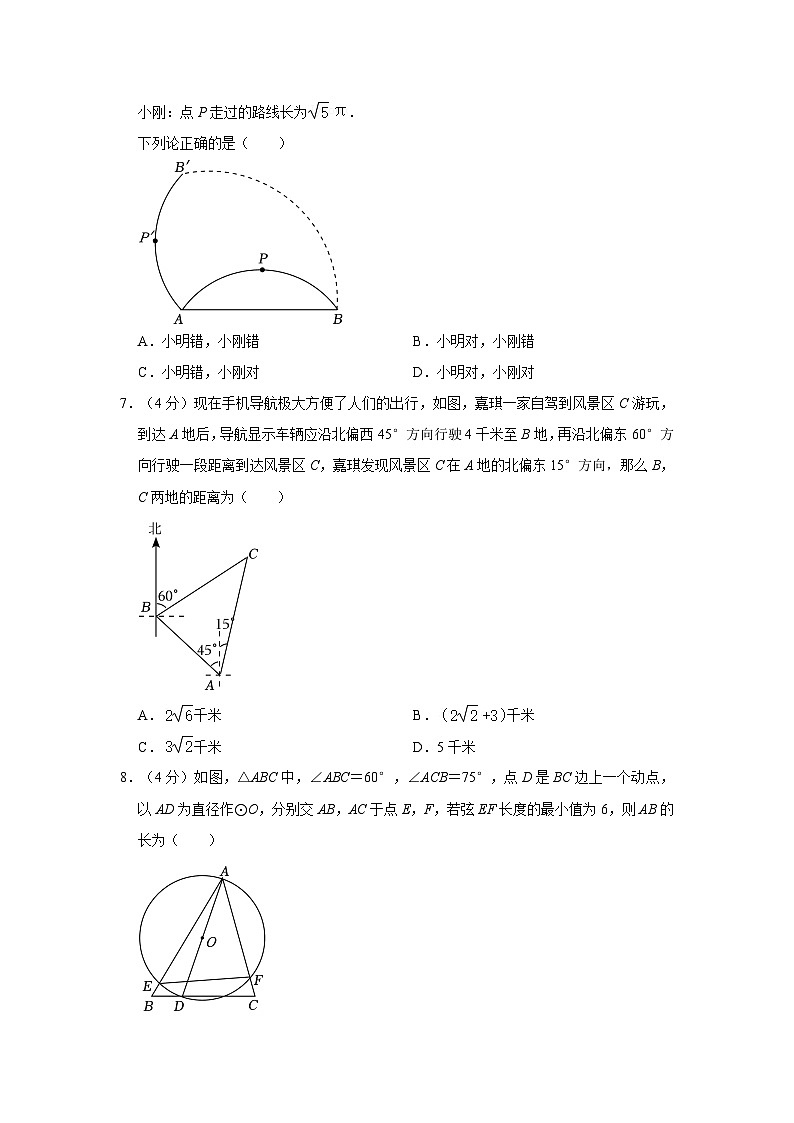
6．（4分）如图，已知所在圆的半径为5，弦AB的长8，点P是的中点，绕点A逆时针旋转90°后得到，两位同学提出了相关结论：
小明：点P到AB的距离为2；
小刚：点P走过的路线长为．
下列论正确的是（ ）
A．小明错，小刚错B．小明对，小刚错
C．小明错，小刚对D．小明对，小刚对
7．（4分）现在手机导航极大方便了人们的出行，如图，嘉琪一家自驾到风景区C游玩，到达A地后，导航显示车辆应沿北偏西45°方向行驶4千米至B地，再沿北偏东60°方向行驶一段距离到达风景区C，嘉琪发现风景区C在A地的北偏东15°方向，那么B，C两地的距离为（ ）
A．千米B．千米
C．千米D．5千米
8．（4分）如图，△ABC中，∠ABC＝60°，∠ACB＝75°，点D是BC边上一个动点，以AD为直径作⊙O，分别交AB，AC于点E，F，若弦EF长度的最小值为6，则AB的长为（ ）
A．B．C．D．
二、选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分.）
9．（5分）如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，下列比值中等于sinA的是（ ）
A．B．C．D．
10．（5分）下列说法正确的是（ ）
A．三点确定一个圆
B．任意三角形有且只有一个内切圆
C．平分弦的直径垂直于这条弦
D．三角形的外心是三边中线的交点
11．（5分）已知方程x2+2x﹣3＝0的解是x1＝1，x2＝﹣3，则给出另一个方程（2x+3）2+2（2x+3）﹣3＝0，它的解是（ ）
A．﹣1或3B．1或3C．﹣1或﹣3D．1或﹣3
（多选）12．（5分）如图，在锐角△ABC中，∠A＝60°，∠ACB＝45°．以BC为弦的⊙O交AG于点D，OD与BC交于点E，若AB与⊙O相切，则下列结论正确的是（ ）
A．DO∥ABB．△BDE∽△BCDC．OD＝ADD．BE＝DE
三、填空题（本大题共4小题，共20分，只要求填写最后结果，每小题填对得5分）
13．（5分）如图，某公园入口处原有三级台阶，每级台阶高为18cm，深为30cm，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现设计斜坡BC的坡度i＝1：5，则AC的长度是 cm．
14．（5分）已知m、n是关于x的方程x2﹣2x﹣1＝0的根，则m2﹣4m﹣2n+2023的值为 ．
15．（5分）已知⊙O的面积为4π，则⊙O的内接正六边形的面积是 ．
16．（5分）如图，在平面直角坐标系中，点A在y轴的正半轴上，OA＝1，将OA绕点O顺时针旋转45°到OA1，扫过的面积记为S1，A1A2⊥OA1交x轴于点A2；将OA2绕点O顺时针旋转45°到OA3，扫过的面积记为S2，A3A4⊥OA3交y轴于点A4；将OA4绕点O顺时针旋转45°到OA5，扫过的面积记为S3，A5A6⊥OA5交x轴于点A6；…；按此规律，则S2023的值为 ．
四、解答题（本大题共7小题，共78分.解答要写出必要的文字说明、证明过程或演算步骤）
17．（10分）（1）计算：2cs45°﹣（sin30°）﹣2+tan30°×tan60°；
（2）用配方法解方程：2m（m﹣2）﹣1＝0．
18．（12分）已知关于x的方程x2﹣5x﹣m2＝0．
（1）求证：方程有两个不相等的实数根；
（2）若方程的两个实数根分别是x1，x2，且x1+2x2＝4，求m的值．
19．（10分）为了办人民满意的教育，某校大门口建造了供家长休息的凉亭（如图1）．图2是抽象出的平面几何图形，已知点D，A，E在同一水平线上，测得∠DAC＝80°，∠BCA＝110°，AC＝2 米．BC＝2.2米．求凉亭最高点B到地面的距离BN的长．
（sin80°⋅≈0.985，cs80°≈0.174，tan80°＝5.671，≈1.732．结果精确到0.01米）
20．（10分）中国是世界上机械发展最早的国家之一，如图1是一辆明代的运输板车，该车沿用宋元制式和包镶式结构，车身选材厚重、纹理精美，低重心的物理结构兼顾了承重性和安金性．如图2是板车侧面的部分示意图，AB为车轮⊙O的直径，过圆心O的车架AC一端点C着地时，地面CD与车轮⊙O相切于点D，连接AD，BD．
（1）求证：∠ADC＝∠DBC．
（2）图2，若测得tan∠BDC＝，CD＝2.4m，求车轮⊙O的半径长．
21．（10分）第19届杭州亚运会于2023年9月23日至10月8日举行，杭州亚运会秉持“绿色、智能、节俭、文明”的办会理念，且亚运会的一套吉祥物是“宸宸”、“琮琮”、“莲莲”．
（1）据市场调研发现，某工厂今年8月份共生产5万套“宸宸”、“琮琮”、“莲莲”，为增大生产量，该工厂平均每月生产量增长率相同，10月份该工厂生产了7.2万套吉祥物，求该工厂平均每月生产量增长率是多少？
（2）已知某商店吉祥物平均每天可销售20套，每套盈利40元，在每套吉祥物降价幅度不超过10元的情况下，每下降2元，则每天可多售10套．如果每天要盈利1440元，则每套吉祥物应降价多少元？
22．（12分）请阅读下面材料，并根据提供的解题思路求解问题：
如图1，在边长为1的正方形网格中，连接格点D，N和E，C，DN和EC相交于点P，求cs∠CPN的值．
【解题思路】
要求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形．观察发现问题中∠CPN不在直角三角形中，我们可以利用网格画平行线等方法解获此类问题，比如连接格点M，N，可发现MN∥EC，则∠DNM＝∠CPN，连接DM，那么∠CPN就变换到Rt△DMN中，进而求出答案．
【解决问题】
（1）根据上述方法归纳，请求图1中cs∠CPN的值；
（2）如图2，在边长为1的正方形网格中，AN与CM相交于点P，求sin∠CPN的值．
23．（14分）如图，AB，CD是⊙O的两条直径，AB⊥CD，点E是劣弧BD上一动点（点E不与B，D重合）．连接AE，CE，分别交OD，OB于点F，G，连接AC．设⊙O的半径为r，∠OAF＝α．
（1）∠OCG＝ （用含a的代数式表示）；
（2）当α＝30°时，求；
（3）判断AG•CF是否为定值．若是，求出该定值；若不是，请说明理由．
2023-2024学年山东省潍坊市寿光市、昌邑市九年级（上）期中数学试卷
参考答案与试题解析
一、选择题（本题共8小题，在每小题给出的四个选项中，只有一个是正确的，每小题选对得4分，共32分，多选、不选、错选均记0分）
1．（4分）若锐角A满足csA＝，则∠A的度数是（ ）
A．30°B．45°C．60°D．75°
【分析】直接利用特殊角的三角函数值进而得出答案．
【解答】解：∵csA＝，
∴∠A＝30°．
故选：A．
【点评】此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键．
2．（4分）方程（x+1）2＝4的解为（ ）
A．x1＝1，x2＝﹣3B．x1＝﹣1，x2＝3
C．x1＝2，x2＝﹣2D．x1＝1，x2＝﹣1
【分析】首先直接开平方可得一元一次方程x+1＝±2，再解即可．
【解答】解：（x+1）2＝4，
x+1＝±2，
则x+1＝2，x+1＝﹣2，
∴x1＝1，x2＝﹣3，
故选：A．
【点评】此题主要考查了直接开平方法解一元二次方程，关键是掌握形如x2＝p或（nx+m）2＝p（p≥0）的一元二次方程可采用直接开平方的方法解一元二次方程．
如果方程化成x2＝p的形式，那么可得x＝±．
3．（4分）用配方法解方程x2+4x+1＝0时，配方结果正确的是（ ）
A．（x﹣2）2＝5B．（x﹣2）2＝3C．（x+2）2＝5D．（x+2）2＝3
【分析】方程整理后，利用完全平方公式配方得到结果，即可作出判断．
【解答】解：方程x2+4x+1＝0，
整理得：x2+4x＝﹣1，
配方得：（x+2）2＝3．
故选：D．
【点评】此题考查了解一元二次方程﹣配方法，熟练掌握完全平方公式是解本题的关键．
4．（4分）如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC＝25°，OC的延长线交PA于点P，则∠P的度数是（ ）
A．25°B．35°C．40°D．50°
【分析】由圆周角定理可求得∠AOP的度数，由切线的性质可知∠PAO＝90°，则可求得∠P．
【解答】解：∵∠ABC＝25°，
∴∠AOP＝2∠ABC＝50°，
∵PA是⊙O的切线，
∴PA⊥AB，
∴∠PAO＝90°，
∴∠P＝90°﹣∠AOP＝90°﹣50°＝40°，
故选：C．
【点评】本题主要考查切线的性质及圆周角定理，根据圆周角定理和切线的性质分别求得∠AOP和∠PAO的度数是解题的关键．
5．（4分）已知点A（a，b）在第四象限，则关于x的一元二次方程ax2+2x+b＝0的根的情况是（ ）
A．没有实数根
B．有两个相等的实数根
C．有两个不相等的实数根
D．无法确定
【分析】先根据点A的位置，判断a，b的正负，从而判断ab的正负，然后求出已知方程根的判别式，进行判断即可．
【解答】解：∵点A（a，b）在第四象限，
∴a＞0，b＜0，
∴ab＜0，
∴﹣4ab＞0，
关于x的一元二次方程ax2+2x+b＝0，
Δ＝b2﹣4ac
＝22﹣4ab
＝4﹣4ab＞0，
∴方程有两个不相等的实数根，
故选：C．
【点评】本题主要考查了一元二次方程根的判别式，解题关键是熟练掌握利用根的判别式判断方程解的情况．
6．（4分）如图，已知所在圆的半径为5，弦AB的长8，点P是的中点，绕点A逆时针旋转90°后得到，两位同学提出了相关结论：
小明：点P到AB的距离为2；
小刚：点P走过的路线长为．
下列论正确的是（ ）
A．小明错，小刚错B．小明对，小刚错
C．小明错，小刚对D．小明对，小刚对
【分析】设所在圆的圆心为O，连接OP、OA，AP'，AP，AB'，根据已知的半径为5，所对的弦AB长为8，点P是的中点，利用垂径定理可得AC＝4，PO⊥AB，再根据勾股定理可得AP的长，利用弧长公式即可求出点P的运动路径长．
【解答】解：设所在圆的圆心为O，连接OP、OA，AP'，AP，AB'，
∵点P是的中点，
∴OP⊥AB，AM＝BM＝AB＝4，
∴OM＝＝3，
∴PM＝5﹣3＝2，
∴点P到AB的距离为2，故小明对，
∵圆O半径为5，所对的弦AB长为8，
根据垂径定理，得
AC＝AB＝4，PO⊥AB，
∴OC＝＝3，
∴PC＝OP﹣OC＝5﹣3＝2，
∴AP＝＝2，
∵将绕点A逆时针旋转90°后得到，
∴∠PAP′＝∠BAB′＝90°，
∴LPP′＝＝π．
则在该旋转过程中，点P的运动路径长是π，故小刚对．
故选：D．
【点评】本题考查了轨迹、垂径定理、勾股定理、圆心角、弧、弦的关系、弧长计算、旋转的性质，解决本题的关键是综合运用以上知识．
7．（4分）现在手机导航极大方便了人们的出行，如图，嘉琪一家自驾到风景区C游玩，到达A地后，导航显示车辆应沿北偏西45°方向行驶4千米至B地，再沿北偏东60°方向行驶一段距离到达风景区C，嘉琪发现风景区C在A地的北偏东15°方向，那么B，C两地的距离为（ ）
A．千米B．千米
C．千米D．5千米
【分析】图所示，过点B作BD⊥AC于D，由题意得，∠BAC＝60°，∠ABC＝75°，利用三角形内角和定理求出∠C＝45°，再求出∠ABD＝30°，∠DBC＝45°＝∠C，得到千米，CD＝BD，利用勾股定理求出千米，即可利用勾股定理求出BC的长．
【解答】解：如图所示，过点B作BD⊥AC于D，
由题意得，∠BAC＝60°，∠ABC＝75°，
∴∠C＝180°﹣∠ABC﹣∠BAC＝45°，
∵BD⊥AC，
∴∠BDC＝∠BDA＝90°，
∴∠ABD＝30°，∠DBC＝45°＝∠C，
∴（千米），CD＝BD，
∴（千米），
∴（千米），
故选：A．
【点评】本题主要考查了勾股定理，等腰直角三角形的性质与判定，含30度角的直角三角形的计算，方位角的表示，正确作出辅助线构造直角三角形是解题的关键．
8．（4分）如图，△ABC中，∠ABC＝60°，∠ACB＝75°，点D是BC边上一个动点，以AD为直径作⊙O，分别交AB，AC于点E，F，若弦EF长度的最小值为6，则AB的长为（ ）
A．B．C．D．
【分析】首先连接OE，OF，过O点作OH⊥EF，垂足为H，可求得半径OE的长，又由当AD为△ABC的边BC上的高时，AD最大时为直径，OE最大，OH最大，EF最小，可求得AD的长，由三角函数的性质，即可求得AB的长．
【解答】解：如图，连接OE，OF，过O点作OH⊥EF，垂足为H，
∴EH＝FH＝EF＝×6＝3，
在△ADB中，∠ABC＝60°，∠ACB＝75°，
∴∠BAC＝45°，
∴∠EOF＝2∠BAC＝90°，
∵OE＝OF，
∴∠EOH＝∠EOF＝45°，
∴OE＝＝3，
∵当AD为△ABC的边BC上的高时，直径AD最短，即OE最小，则EF最小，
∴AD＝2OE＝6，
∴AB＝＝＝4．
故选：B．
【点评】此题考查了圆周角定理、勾股定理以及三角函数的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
二、选择题（本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分.）
9．（5分）如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，下列比值中等于sinA的是（ ）
A．B．C．D．
【分析】利用锐角三角函数定义判断即可．
【解答】解：在Rt△ABC中，sinA＝，
在Rt△ACD中，sinA＝，
∵∠A+∠B＝90°，∠B+∠BCD＝90°，
∴∠A＝∠BCD，
在Rt△BCD中，sin∠BCD＝sinA＝．
故选：B．
【点评】此题考查了锐角三角函数的定义，熟练掌握锐角三角函数定义是解本题的关键．
10．（5分）下列说法正确的是（ ）
A．三点确定一个圆
B．任意三角形有且只有一个内切圆
C．平分弦的直径垂直于这条弦
D．三角形的外心是三边中线的交点
【分析】根据三角形的外接圆及垂径定理可得出答案．
【解答】解：A．不在同一条直线上的三个点确定一个圆，原说法错误，不符合题意；
B．任意三角形有且只有一个内切圆，原说法正确，符合题意；
C．平分弦（不是直径）的直径垂直于弦，原说法错误，不符合题意；
D．三角形的外心是三边垂直平分线的交点，原说法正确，符合题意；
故选：B．
【点评】本题考查了三角形的外接圆与外心，垂径定理，确定圆的条件，熟记概念及性质是解题关键．
11．（5分）已知方程x2+2x﹣3＝0的解是x1＝1，x2＝﹣3，则给出另一个方程（2x+3）2+2（2x+3）﹣3＝0，它的解是（ ）
A．﹣1或3B．1或3C．﹣1或﹣3D．1或﹣3
【分析】先根据已知方程和方程的解，从而得到方程（2x+3）2+2（2x+3）﹣3＝0中的2x+3相当于第1个方程中的x，从而得到2x+3＝1和2x+3＝﹣3，解方程即可．
【解答】解：∵方程x2+2x﹣3＝0的解是x1＝1，x2＝﹣3，
∴方程（2x+3）2+2（2x+3）﹣3＝0，
2x+3＝1，2x+3＝﹣3，
2x＝﹣2，2x＝﹣6，
x1＝﹣1，x2＝﹣3，
故选：C．
【点评】本题主要考查了一元二次方程的解，解题关键是熟练掌握利用换元法解一元二次方程．
（多选）12．（5分）如图，在锐角△ABC中，∠A＝60°，∠ACB＝45°．以BC为弦的⊙O交AG于点D，OD与BC交于点E，若AB与⊙O相切，则下列结论正确的是（ ）
A．DO∥ABB．△BDE∽△BCDC．OD＝ADD．BE＝DE
【分析】由切线的性质得∠ABO＝90°，而∠BOD＝2∠ACB＝90°，所以∠BOD+∠ABO＝180°，则DO∥AB，可判断A正确；由等腰直角三角形的性质得∠ODB＝∠OBD＝45°，所以∠EDB＝∠DCB＝45°，而∠EBD＝∠DBC，则△BDE∽△BCD，可判断B正确；作DF⊥AB于点F，则DF＝OB＝OD，由DF＜AD，得OD＜AD，可判断C错误；连接OC，可证明△COD是等边三角形，则OD＝CD，所以BD＝OD＝CD，由△BDE∽△BCD，得＝，于是得＝＝，所以BE＝DE，可判断D正确，于是得到问题的答案．
【解答】解：∵AB与⊙O相切于点B，
∴AB⊥OB，
∴∠ABO＝90°，
∵∠ACB＝45°，
∴∠BOD＝2∠ACB＝90°，
∴∠BOD+∠ABO＝180°，
∴DO∥AB，
故A正确；
∵OB＝OD，∠BOD＝90°，
∴∠ODB＝∠OBD＝45°，
∴∠EDB＝∠DCB＝45°，
∵∠EBD＝∠DBC，
∴△BDE∽△BCD，
故B正确；
作DF⊥AB于点F，则DF＝OB＝OD，
∵DF＜AD，
∴OD＜AD，
故C错误；
连接OC，则OC＝OD，
∵∠ODC＝∠A＝60°，
∴△COD是等边三角形，
∴OD＝CD，
∴BD＝＝＝OD＝CD，
∵△BDE∽△BCD，
∴＝，
∴＝＝，
∴BE＝DE，
故D正确，
故选：ABD．
【点评】此题重点考查切线的性质、勾股定理、平行线的判定与性质、等边三角形的判定与性质、相似三角形的判定与性质、垂线段最短等知识，正确地作出所需要的辅助线是解题的关键．
三、填空题（本大题共4小题，共20分，只要求填写最后结果，每小题填对得5分）
13．（5分）如图，某公园入口处原有三级台阶，每级台阶高为18cm，深为30cm，为方便残疾人士，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现设计斜坡BC的坡度i＝1：5，则AC的长度是 210 cm．
【分析】首先过点B作BD⊥AC于D，根据题意即可求得AD与BD的长，然后由斜坡BC的坡度i＝1：5，求得CD的长，继而求得答案．
【解答】解：过点B作BD⊥AC于D，
根据题意得：AD＝2×30＝60（cm），BD＝18×3＝54（cm），
∵斜坡BC的坡度i＝1：5，
∴BD：CD＝1：5，
∴CD＝5BD＝5×54＝270（cm），
∴AC＝CD﹣AD＝270﹣60＝210（cm）．
∴AC的长度是210cm．
故答案为：210．
【点评】此题考查了解直角三角形的应用：坡度问题．此题难度适中，注意掌握坡度的定义，注意数形结合思想的应用与辅助线的作法．
14．（5分）已知m、n是关于x的方程x2﹣2x﹣1＝0的根，则m2﹣4m﹣2n+2023的值为 2020 ．
【分析】根据一元二次方程解的定义及根与系数的关系得出m2﹣2m＝1，m+n＝2，将原式化简求值即可．
【解答】解：∵m、n是关于x的方程x2﹣2x﹣1＝0的根，
∴m2﹣2m＝1，m+n＝2，
∴m2﹣4m﹣2n+2023
＝m2﹣2m﹣2（m+n）+2023
＝1﹣2×2+2023
＝2020．
故答案为：2020．
【点评】本题主要考查一元二次方程的根及根与系数的关系以及一元二次方程的解，熟练掌握一元二次方程根与系数的关系是解题关键．
15．（5分）已知⊙O的面积为4π，则⊙O的内接正六边形的面积是 6 ．
【分析】过点O作OH⊥AB于点H，连接OA，OB，先求出⊙O的半径，又由圆的内接正六边形的性质，即可求得答案．
【解答】解：∵⊙O的面积为4π，
∴⊙O的半径为2，
过点O作OH⊥AB于点H，连接OA，OB，
∴AH＝AB，
∵∠AOB＝×360°＝60°，OA＝OB，
∴△OAB是等边三角形，
∴AB＝OA＝2，
∴AH＝OA＝1，
∴OH＝AH＝，
∴S正六边形ABCDEF＝6S△OAB＝6××2×＝6，
故答案为：6．
【点评】本题考查的是正多边形和圆，熟知正六边形的半径与边长相等是解答此题的关键．
16．（5分）如图，在平面直角坐标系中，点A在y轴的正半轴上，OA＝1，将OA绕点O顺时针旋转45°到OA1，扫过的面积记为S1，A1A2⊥OA1交x轴于点A2；将OA2绕点O顺时针旋转45°到OA3，扫过的面积记为S2，A3A4⊥OA3交y轴于点A4；将OA4绕点O顺时针旋转45°到OA5，扫过的面积记为S3，A5A6⊥OA5交x轴于点A6；…；按此规律，则S2023的值为 22019π ．
【分析】根据旋转的性质，得到△A1OA2、△A3OA4、△A5OA6、⋯、都是等腰直角三角形，分别求出 ，OA4＝2，，利用扇形面积求出S1，S2，S3，S4，抽象概括出相应的数字规律，进而得出结论即可．
【解答】解：将OA绕点O顺时针旋转45°到OA1，A1A2⊥OA1交x轴于点A2
∴∠AOA1＝45°，OA＝OA1＝1，∠OA1A2＝90°，
∴∠A1OA2＝90°﹣∠AOA1＝45°，
∴∠OA2A1＝90°﹣∠A1OA2＝45°，
∴△A1OA2是等腰直角三角形，
∴A1A2＝OA1＝1，
∴；
同理可得：△A3OA4、△A5OA6、⋯、都是等腰直角三角形，OA4＝2，…，
∴，，，，⋯；
∴，
∴，
故答案为：22019π．
【点评】本题考查坐标与旋转，等腰三角形的判定和性质，扇形的面积．熟练掌握旋转的性质，扇形的面积公式，抽象概括出相应的数字规律，是解题的关键．
四、解答题（本大题共7小题，共78分.解答要写出必要的文字说明、证明过程或演算步骤）
17．（10分）（1）计算：2cs45°﹣（sin30°）﹣2+tan30°×tan60°；
（2）用配方法解方程：2m（m﹣2）﹣1＝0．
【分析】（1）将特殊角的三角函数值代入计算即可；
（2）利用配方法得到（m﹣1）2＝，然后利用直接开平方法解方程．
【解答】解：（1）原式＝2×﹣（）﹣2+×
＝﹣4+1
＝﹣3；
（2）原方程化为m2﹣2m＝，
配方，得m2﹣2m+1＝+1，
即（m﹣1）2＝，
∴m﹣1＝±，
∴m1＝1+，m2＝1﹣．
【点评】本题考查了特殊角的三角函数值和解一元二次方程﹣配方法，解答本题的关键是掌握几个特殊角的三角函数值和配方法的步骤．
18．（12分）已知关于x的方程x2﹣5x﹣m2＝0．
（1）求证：方程有两个不相等的实数根；
（2）若方程的两个实数根分别是x1，x2，且x1+2x2＝4，求m的值．
【分析】（1）证明判别式的值大于0即可；
（2）首先求出x2＝﹣1，再代入方程求出m即可．
【解答】（1）证明：∵Δ＝（﹣5）2﹣4×1×（﹣m2）＝25+4m2＞0，
∴方程有两个不相等的实数根；
（2）解：∵方程的两个实数根分别是x1，x2，
∴x1+x2＝5，
∵x1+2x2＝4，
∴5+x2＝4，
∴x2＝﹣1，
∴1+5﹣m2＝0，
∴m2＝6，
∴m＝±．
【点评】本题考查根与系数关系，根的判别式等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
19．（10分）为了办人民满意的教育，某校大门口建造了供家长休息的凉亭（如图1）．图2是抽象出的平面几何图形，已知点D，A，E在同一水平线上，测得∠DAC＝80°，∠BCA＝110°，AC＝2 米．BC＝2.2米．求凉亭最高点B到地面的距离BN的长．
（sin80°⋅≈0.985，cs80°≈0.174，tan80°＝5.671，≈1.732．结果精确到0.01米）
【分析】过点C作CG⊥DE于点G，过点B作BF⊥GC交GC的延长线于点F，在Rt△ACG与Rt△BFC中，分别通过解直角三角形求出CG与FC的长即可求解．
【解答】解：如图，过点C作CG⊥DE于点G，过点B作BF⊥GC交GC的延长线于点F，
则GF＝BN，
∵sin∠DAC＝＝sin80°≈0.985，AC＝2米，
∴CG＝2×0.985＝1.97（米），
∵∠DAC＝80°，
∴∠ACG＝10°，
又∵∠BCA＝110°，
∴∠BCF＝60°，
又∵BC＝2.2米，
∴FC＝BC•cs60°＝2.2×＝1.1（米），
∴GF＝GC+CF＝1.97+1.1＝3.07（米）．
∴凉亭最高点B到地面的距离BN的长约为3.07米．
【点评】本题考查了解直角三角形的应用，正确作出辅助线构造直角三角形是解题的关键．
20．（10分）中国是世界上机械发展最早的国家之一，如图1是一辆明代的运输板车，该车沿用宋元制式和包镶式结构，车身选材厚重、纹理精美，低重心的物理结构兼顾了承重性和安金性．如图2是板车侧面的部分示意图，AB为车轮⊙O的直径，过圆心O的车架AC一端点C着地时，地面CD与车轮⊙O相切于点D，连接AD，BD．
（1）求证：∠ADC＝∠DBC．
（2）图2，若测得tan∠BDC＝，CD＝2.4m，求车轮⊙O的半径长．
【分析】（1）由直径所对的角成90°，CD是⊙O的切线等条件，可证；
（2）圆心角所对的弧度等于圆周角的两倍，运用二倍角公式可求．
【解答】（1）证明：
∵AB为车轮⊙O的直径，
∴∠ADB＝90°，∠ADO+∠ODB＝90°，
∵地面CD与车轮⊙O相切于点D，
∴OD⊥CD，∠ODC＝90，∠ODB+∠BDC＝90°，
∴∠ADO＝∠BDC，
∵OA＝OD，
∴∠A＝∠ADO＝∠BDC，
∵∠DBC＝∠A+∠ADB＝∠A+∠ADO+∠ODB，
∴∠DBC＝∠ADO+∠ODB+∠BDC，∠ADC＝∠ADC+∠ODB+∠BDC，
∴∠DBC＝∠ADC；
（2）解：∵∠BDC＝∠A，
∴tan∠A＝tan∠BDC＝，
∵∠DOB＝2∠A，
∴tan∠DOB＝tan2∠A＝＝，
∵CD＝2.4m，
∴在Rt△ODC中，OD＝＝0.54m，
∴车轮⊙O的半径长0.54m．
【点评】本题考查了解直角三角形，关键是对圆的条件熟练运用．
21．（10分）第19届杭州亚运会于2023年9月23日至10月8日举行，杭州亚运会秉持“绿色、智能、节俭、文明”的办会理念，且亚运会的一套吉祥物是“宸宸”、“琮琮”、“莲莲”．
（1）据市场调研发现，某工厂今年8月份共生产5万套“宸宸”、“琮琮”、“莲莲”，为增大生产量，该工厂平均每月生产量增长率相同，10月份该工厂生产了7.2万套吉祥物，求该工厂平均每月生产量增长率是多少？
（2）已知某商店吉祥物平均每天可销售20套，每套盈利40元，在每套吉祥物降价幅度不超过10元的情况下，每下降2元，则每天可多售10套．如果每天要盈利1440元，则每套吉祥物应降价多少元？
【分析】（1）设该工厂平均每月生产量增长率为x，根据某工厂今年8月份共生产5万套“宸宸”、“琮琮”、“莲莲”，10月份该工厂生产了7.2万套吉祥物，列出一元二次方程，解之取其正值即可；
（2）设每套吉祥物应降价a元，则每天销售量为（20+5a）套，每套盈利为（40﹣a）元，根据每天要盈利1440元，列出一元二次方程，解之取符合题意的值即可．
【解答】解：（1）设该工厂平均每月生产量增长率是x，
由题意得：5（1+x）2＝7.2，
解得：x1＝0.2＝20%，x2＝﹣2.2（舍去），
答：该工厂平均每月生产量增长率是20%；
（2）设每套吉祥物应降价a元（0≤a≤10），则每天销售量为（20+5a）套，每套盈利为（40﹣a）元，
由题意得：（20+5a）（40﹣a）＝1440，
整理得：a2﹣36a+128＝0，
解得：a1＝4，a2＝32（不符合题意，舍去），
答：每套吉祥物应降价4元．
【点评】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．
22．（12分）请阅读下面材料，并根据提供的解题思路求解问题：
如图1，在边长为1的正方形网格中，连接格点D，N和E，C，DN和EC相交于点P，求cs∠CPN的值．
【解题思路】
要求一个锐角的三角函数值，我们往往需要找出（或构造出）一个直角三角形．观察发现问题中∠CPN不在直角三角形中，我们可以利用网格画平行线等方法解获此类问题，比如连接格点M，N，可发现MN∥EC，则∠DNM＝∠CPN，连接DM，那么∠CPN就变换到Rt△DMN中，进而求出答案．
【解决问题】
（1）根据上述方法归纳，请求图1中cs∠CPN的值；
（2）如图2，在边长为1的正方形网格中，AN与CM相交于点P，求sin∠CPN的值．
【分析】（1）连接格点M，N，D，先利用勾股定理及逆定理判断△DMN的形状，再判断CE、MN的关系，最后在直角△DMN中利用直角三角形的边角间关系得结论；
（2）连接格点N、G、A，先利用勾股定理及逆定理判断△AGN的形状，再判断CM、AG的关系，最后在直角△AGN中利用直角三角形的边角间关系得结论．
【解答】解：（1）如图1所示：连接格点M，N，D．
∵点M、N、D都在格点上，
∴DN＝＝，MN＝＝，
DM＝＝2．
∵∠ECN＝∠MNK＝45°，
∴MN∥EC．
∴∠DNM＝∠CPN．
∵DM2+MN2＝8+2＝10，DN2＝10，
∴DM2+MN2＝DN2．
∴△DMN是直角三角形．
在Rt△DMN中，
cs∠CPN＝cs∠DNM
＝
＝
＝
＝．
（2）如图2所示：连接格点N、G、A．
∵点N、G、A在格点上，
∴AG＝GN＝＝，
AN＝＝．
∵AG2+GN2＝2+2＝10，AN2＝10，
∴AG2+GN2＝AN2．
∴△AGN是直角三角形．
∵tan∠CMK＝tan∠GAK＝2，
∴∠CMK＝∠GAK．
∴AG∥CM．
∴∠CPN＝∠GAN．
在Rt△AGN中，
∴sin∠CPN＝sin∠GAN
＝
＝
＝．
【点评】本题考查了解直角三角形，掌握勾股定理及其逆定理、平行线的判定和性质、直角三角形的边角间关系等知识点是解决本题的关键．
23．（14分）如图，AB，CD是⊙O的两条直径，AB⊥CD，点E是劣弧BD上一动点（点E不与B，D重合）．连接AE，CE，分别交OD，OB于点F，G，连接AC．设⊙O的半径为r，∠OAF＝α．
（1）∠OCG＝ 45°﹣α （用含a的代数式表示）；
（2）当α＝30°时，求；
（3）判断AG•CF是否为定值．若是，求出该定值；若不是，请说明理由．
【分析】（1）由题意得出∠AEC＝45°，再由三角形的内角和即可解答；
（2）过点A作AH⊥CE于点H，由（1）可得∠OCG＝15°，∠ACE＝60°，由直角三角形的性质可得出答案；
（3）AG•CF是定值，AG•CF＝AC2＝2r2，由△ACF∽△GAC，得出即可求解．
【解答】解：（1）∵AB⊥CD，
∴∠AOC＝90°，∠ACO+∠CAO＝45°，
∴∠AEC＝45°，
∴∠OAF+∠OCG＝180°﹣45°﹣90°，
∴∠OCG＝45°﹣∠OAF＝45°﹣α，
故答案为：45°﹣α；
（2）过点A作AH⊥CE于点H，
∵∠OAF＝α＝30°．
∴∠OCG＝45°﹣30°＝15°，
∵AB⊥CD，OA＝OC，
∴∠ACD＝45°，
∴∠ACE＝∠ACD+∠OCG＝60°，
∵∠AEC＝45°，
∴AH＝EH，
设CH＝x，则AC＝2x，AH＝x，
∴AE＝AH＝x，
∴；
（3）AG•CF是定值，AG•CF＝AC2＝2r2，
由题意知，∠ACG＝∠ACD+∠DCE＝45°+∠DCE，∠AFC＝∠D+∠DAE＝45°+∠DAE，
∵∠DCE＝∠DAE，
∴∠ACG＝∠AFC，
又∵∠ACF＝∠CAG＝45°，
∴△ACF∽△GAC，
∴，
∴AG•CF＝AC2，
∵OA＝OC＝r，
∴AC＝r，
∴AC2＝2r2，
即AG•CF＝AC2＝2r2．
【点评】本题考查圆周角定理和相似三角形的性质，含30°角的直角三角形的性质，等腰直角三角形的性质，熟练掌握以上性质是解题关键．