2023届新疆维吾尔自治区喀什地区疏勒县实验学校高三上学期期中数学（文）试题含解析

这是一份2023届新疆维吾尔自治区喀什地区疏勒县实验学校高三上学期期中数学（文）试题含解析，共16页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．设集合，则（ ）
A．B．C．D．
【答案】B
【分析】求出集合后可求.
【详解】，故，
故选：B.
2．下列说法中，不正确的是（ ）
A．已知，命题：“若，则”为真命题
B．命题：“”的否定是：“”
C．命题“或”为真命题，则命题和命题均为真命题
D．“”是“”的充分不必要条件
【答案】C
【分析】利用常用逻辑用语的相关知识逐一分析判断即可.
【详解】A，由题意，则不等式两边同除以，可得，故A正确；
B，命题“”的否定是：“”，故B正确；
C，命题“或”为真命题，则命题和命题q至少由一个为真命题，故C错误；
D，，反之不成立，因此是的充分不必要条件，故D正确.
故选C．
3．若变量x，y满足约束条件，则目标函数的最小值为（ ）
A．1B．-2C．-5D．-7
【答案】C
【分析】画出可行域，向上平移基准直线到可行域边界位置，由此求得目标函数的最小值.
【详解】画出可行域如下图所示，向上平移基准直线 到可行域边界的位置，由此求得目标函数的最小值为.
故选：C.
【点睛】本小题主要考查利用线性规划求目标函数的最小值，考查数形结合的数学思想方法，属于基础题.
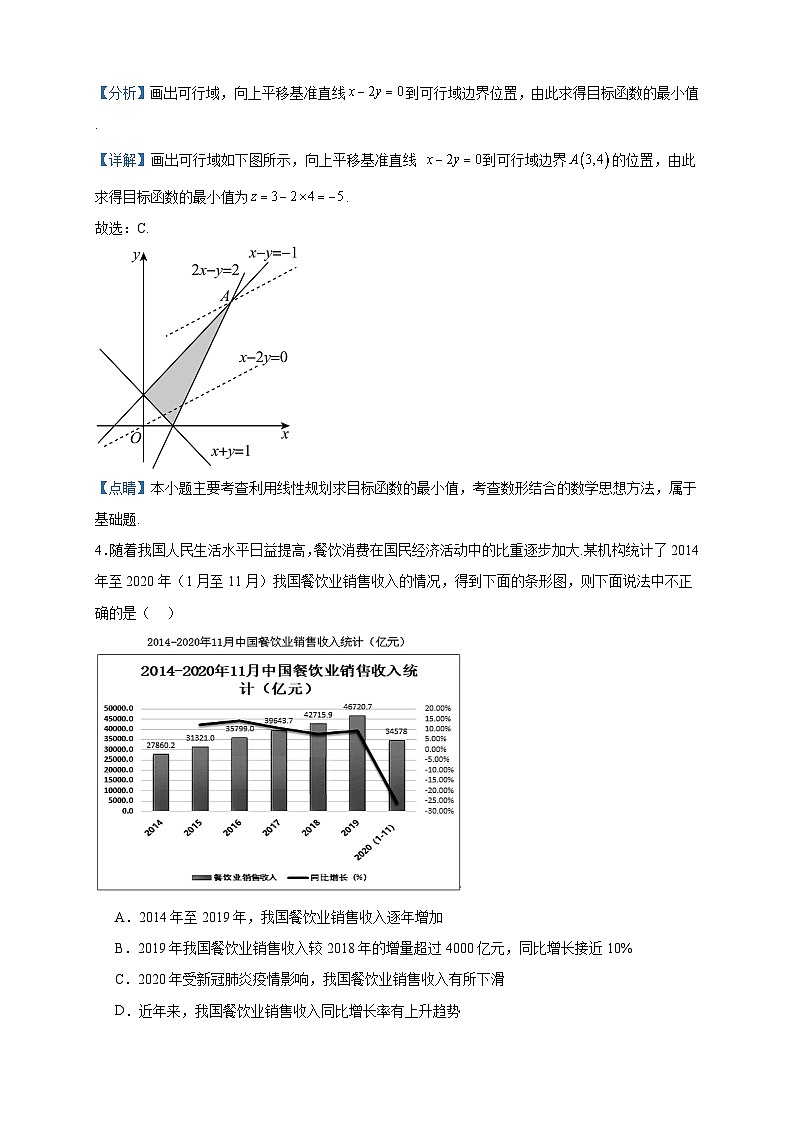
4．随着我国人民生活水平日益提高，餐饮消费在国民经济活动中的比重逐步加大.某机构统计了2014年至2020年（1月至11月）我国餐饮业销售收入的情况，得到下面的条形图，则下面说法中不正确的是（ ）
A．2014年至2019年，我国餐饮业销售收入逐年增加
B．2019年我国餐饮业销售收入较2018年的增量超过4000亿元，同比增长接近10%
C．2020年受新冠肺炎疫情影响，我国餐饮业销售收入有所下滑
D．近年来，我国餐饮业销售收入同比增长率有上升趋势
【答案】D
【分析】结合给出的销售统计收入情况，依次分析选项即可得解.
【详解】对于A，从条形图可以看出，2014年至2019年，我国餐饮业销售收入逐年增加，故A正确；
对于B，2018年和2019年我国餐饮业销售收入分别为亿元和亿元，2019年较2018年多增量为亿元，从折线图可以看出，同比增长接近（实际增长为），故B正确；
对于C，从条形图可以看出，2020年我国餐饮业销售收入有所下滑，故C正确；
对于D，从折线图可以看出，我国餐饮业销售收入同比增长率并没有上升趋势，故D错误.
5．已知，，，则（ ）
A．B．C．D．
【答案】D
【分析】三个数分别和1比较大小，再结合单调性比较，即可得三个数的大小.
【详解】，
所以.
故选：D
6．下面程序框图的算术思路源于《几何原本》中的“辗转相除法”（如图），若输入，则输出的为
A．B．C．D．
【答案】D
【详解】第1次执行循环体， ，不满足退出循环的条件；
第2次执行循环体， 不满足退出循环的条件；
第3次执行循环体， ，不满足退出循环的条件；
第4次执行循环体， ，满足退出循环的条件；
故输出的值为5．
故选D．
7．函数的图象大致是（ ）
A．B．
C．D．
【答案】B
【分析】先根据函数的奇偶性排除部分选项，然后令y=0，结合图象分析求解.
【详解】因为函数定义域为R，且，所以函数是奇函数，故排除C，
由，令y=0得x=-1，x=0，x=1，当时，，当时，，排除AD
故选：B
【点睛】本题主要考查函数图象的识别以及函数的奇偶性和零点的应用，还考查了数形结合的思想和分析求解问题的能力，属于中档题.
8．设，为两个平面，则的充要条件是
A．内有无数条直线与平行
B．内有两条相交直线与平行
C．，平行于同一条直线
D．，垂直于同一平面
【答案】B
【分析】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．
【详解】由面面平行的判定定理知：内两条相交直线都与平行是的充分条件，由面面平行性质定理知，若，则内任意一条直线都与平行，所以内两条相交直线都与平行是的必要条件，故选B．
【点睛】面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若，则”此类的错误．
9．若，且在第四象限，则（ ）
A．B．C．D．
【答案】D
【解析】由已知利用同角三角函数基本关系式即可计算得解．
【详解】解：∵，且在第四象限，
∴，
∴．
故选：D．
10．已知向量，满足，，且，则，的夹角大小为（ ）．
A．B．C．D．
【答案】C
【分析】根据向量的数量积的运算，求得，再结合向量的夹角公式，即可求解.
【详解】由题意，向量，满足，，
因为，可得，解得，
设，的夹角大小为，所以，
因为，所以．
故选：C.
11．函数，则下列结论错误的是（ ）
A．的一个周期为B．在单调递减
C．图像关于直线对称D．的一个零点为
【答案】C
【分析】根据周期公式可判断A；由正弦函数单调性可判断B；根据对称轴所对应的函数为最值可判断C；计算是否为0可判断D．
【详解】A中，因为周期，，所以是周期，A正确；
B中，令得
令得，所以在上单调递减，故在单调递减正确，B正确；
C中，因为，故直线不是对称轴，故C错；
D中，因为，所以的一个零点为正确，
故选：C．
12．直线是曲线的一条切线，则实数k的值为（ ）
A．B．C．1D．
【答案】A
【分析】设切点为，求出函数的导函数，即可求出切线方程，再根据切线过定点，即可求出，从而求出切线的斜率；
【详解】解：设切点为，
由，得，则，
则曲线在切点处的切线方程为，
由已知可得，切线过定点，
代入切线方程可得：，解得，
则.
故选：A.
二、填空题
13．若复数满足： ，则复数的虚部是 ．
【答案】；
【分析】根据复数及模的定义计算即可.
【详解】设 ，由题意 得： ，
，解得 ,其虚部为-1；
故答案为：-1.
14．，，分别为内角，，的对边．已知，则 ．
【答案】
【分析】由余弦定理和已知可得答案.
【详解】因为，且，所以．
故答案为：.
15．如果生男孩和生女孩的概率相等，则有3个小孩的家庭中女孩多于男孩的概率为 ．
【答案】
【解析】根据独立重复试验的概率计算公式即可求解.
【详解】设女孩个数为X，女孩多于男孩的概率为
P(X≥2)＝P(X＝2)＋P(X＝3)＝.
故答案为：
16．若函数的定义域是，则函数的定义域为 ．
【答案】
【分析】由函数y=f（x）的定义域为[，2]，知≤lg2x≤2，由此能求出函数y=f（lg2x）的定义域即可．
【详解】∵函数y=f（x）的定义域为[，2]，
∴≤lg2x≤2，
∴≤x≤4．
故答案为：
【点睛】本题主要考查函数的定义域和对数不等式的解法，意在考查学生对这些知识的掌握水平和分析推理能力.
三、解答题
17．△ABC的内角A，B，C的对边分别为a，b，c，已知.
(1)求B；
(2)若，，求c.
【答案】(1)；
(2)
【分析】（1）由正弦定理化简条件，求得，从而求得角B.
（2）将条件，代入余弦定理求得c.
【详解】（1）因为，所以，
即，
化简得，所以，
又因为，所以.
（2）因为，
所以，
整理得，解得.
18．已知是公差为3的等差数列，数列满足．
（Ⅰ）求的通项公式； （Ⅱ）求的前n项和．
【答案】(Ⅰ);(Ⅱ)见解析.
【详解】试题分析：（Ⅰ）用等差数列通项公式求；（Ⅱ）求出通项，再利用等比数列求和公式来求.
试题解析：（Ⅰ）由已知，得，所以数列是首项为2，公差为3的等差数列，通项公式为.
（Ⅱ）由（Ⅰ）和 得，因此是首项为1，公比为的等比数列.记的前项和为，则
【解析】等差数列与等比数列
【名师点睛】等差、等比数列各有五个基本量,两组基本公式,而这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化为解关于基本量的方程（组）,因此可以说数列中的绝大部分运算题可看作方程应用题,所以用方程思想解决数列问题是一种行之有效的方法.
19．某市从2020年5月1日开始，若电子警察抓拍到机动车不礼让行人的情况后，交警部门将会对不礼让行人的驾驶员进行扣3分，罚款200元的处罚，并在媒体上曝光.但作为交通重要参与者的行人，闯红灯通行却频有发生，带来了较大的交通安全隐患和机动车通畅率降低点情况.交警部门在某十字路口根据以往的监测数据，得到行人闯红灯的概率为0.2，并从穿越该路口的行人中随机抽取了200人进行调查，对是否存在闯红灯的情况进行统计，得到2×2列联表如下：
近期，为了整顿“行人闯红灯”这一不文明的违法行为，交警部门在该十字路口试行了对闯红灯的行人进行5元以上，50元以下的经济处罚.在试行经济处罚一段时间后，交警部门再次对穿越该路口的行人中随机抽取了200人进行调查，对是否存在闯红灯的情况进行统计，得到列联表如下：
将统计数据所得频率视为概率，完成下列问题：
(1)将列联表填写完整（不需要写出填写过程），并根据表中数据分析，在试行对闯红灯的行人进行经济处罚前，是否有的把握认为闯红灯行为与年龄有关；
(2)在试行对闯红灯的行人进行经济处罚后，闯红灯现象是否有明显改善，请说明理由；
参考公式：，其中.
参考数据：
【答案】(1)列联表见解析，有的把握认为闯红灯行为与年龄有关
(2)试行对闯红灯的行人进行经济处罚后，闯红灯现象有明显改善.
【分析】（1）根据题意，得出的列联表，利用公式求得的值，结合附表，即可求解；
（2）求得试行对闯红灯的行人进行经济处罚后，行人闯红灯的概率，结合试行对闯红灯的行人进行经济处罚前的概率，即可得出结论.
【详解】（1）解：根据题意，可得得到列联表如下：
则，
所以有的把握认为闯红灯行为与年龄有关.
（2）解：在试行对闯红灯的行人进行经济处罚后，行人闯红灯的概率为，
而在试行对闯红灯的行人进行处罚前，行人闯红灯的概率为，
所以在试行对闯红灯的行人进行经济处罚后，闯红灯现象有明显改善.
20．如图，在平行四边形ABCD中，，，，四边形ABEF为直角梯形，，，，，平面平面ABEF．
（1）求证：平面ABEF．
（2）求平面ABCD与平面DEF所成锐二面角的余弦值．
【答案】（1）证明见解析；（2）．
【分析】（1）在中，利用余弦定理求出，然后由勾股定理可得，结合面面垂直的性质定理证明即可；
（2）利用面面垂直的性质定理证得平面，建立合适的空间直角坐标系，求出所需点的坐标和向量，利用待定系数法求出平面的法向量，然后利用向量的夹角公式求解即可．
【详解】（1）证明：在中，∵，，，所以，
∴，即．
又∵平面平面，
且平面平面，平面，
∴平面；
（2）解：由平面平面，
平面平面，
可得平面，
又由（1）知平面．
以A为坐标原点，分别以AB，AF，AC所在直线为x，y，z轴建立空间直角坐标系．
则，，，，，，，
设平面的一个法向量为，
由取，得；
是平面的一个法向量．
设平面与平面所成锐二面角为，
则．
即平面ABCD与平面DEF所成锐二面角的余弦值为．
21．已知函数．
（1）若，求的单调区间；
（2）证明：只有一个零点．
【答案】（1）增区间是，，减区间是；
（2）证明见解析.
【分析】（1）将代入，求导得，令求得增区间，令求得减区间；
（2）令，即，则将问题转化为函数只有一个零点问题，研究函数单调性可得.
【详解】（1）当a=3时，，．
令解得x=或x=．
由解得：；
由解得：．
故函数的增区间是，，减区间是．
（2）［方法一］：【最优解】【通性通法】等价转化＋零点存在性定理
由于，所以等价于．
设,则,仅当时,所以在单调递增.故至多有一个零点,从而至多有一个零点.又,故有一个零点.综上,只有一个零点.
［方法二］：函数零点与图象交点个数的关系
因为，所以等价于，令，则．因为，则，当且仅当时，等号成立，所以在区间内单调递增，
当时，；当时，．所以直线与的图像只有一个交点，即只有一个零点．
［方法三］：【通性通法】含参分类讨论＋零点存在性定理
．
①当时，单调递增，只有一个零点．
②当与时，，再令或，则有．当与时，单调递增，当时，单调递减．
因为，
，
所以．
极大值与极小值同正同负，故只有一个零点．
［方法四］： 等价转化＋零点存在性定理
由于，所以，等价于．
设，则，仅当时，，所以在区间内单调递增．故至多有一个零点，从而至多有一个零点．
结合函数与方程的关系，根据零点存在性定理，取，则有，取，则有，所以在内有一个零点，故有一个零点．
综上，只有一个零点．
【整体点评】（2）方法一：通过分离参数将原函数的零点问题转化为易求单调性的函数零点问题，该法既是该类型题的通性通法，也是该题的最优解；
方法二：将函数的零点个数问题转化为两函数图象的交点个数问题，是常见的解题思路，对于证明题，这种方式显得不是特别严谨；
方法三：直接对参数分类讨论，研究函数的单调性和最值，也是该类型问题的通性通法，但对于该题，显得有些复杂；
方法四：该法同方法一，只是在零点存在性定理的运用过程中取点不一样．
22．直角坐标系中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为．
(1)将曲线C的极坐标方程化为直角坐标方程；
(2)设点A的直角坐标为为C上的动点，点P是线段的中点，求点P轨迹的极坐标方程．
【答案】(1)
(2)
【分析】（1）根据极坐标方程与直角坐标方程的转化公式，直接求得答案.
（2）设出M的坐标，利用中点坐标公式表示出点P的坐标，化简可得其参数方程，继而可化为普通方程，再化为极坐标方程.
【详解】（1）曲线C的极坐标方程为，
化为直角坐标方程为，即为．
（2）设，
又，由中点坐标公式可得，
化为参数方程为（为参数），
化为普通方程为，
故化为极坐标方程为.
23．已知函数的最小值为m．
(1)求m的值；
(2)设均为正数，，求的最小值．
【答案】(1)
(2)1
【分析】（1）将写成分段函数的形式，求出分段函数的最小值，即可得到结果；
（2）由（1）可知，再利用由柯西不等式，即可得到结果.
【详解】（1）解：
当时，；
当时，；
当时，；
综上，，故．
（2）解：，由柯西不等式可得：
，
，当组仅当即时，
的最小值为1．
45岁以下
45岁以上
合计
闯红灯人数
25
未闯红灯人数
85
合计
200
45岁以下
45岁以上
合计
闯红灯人数
5
15
20
未闯红灯人数
95
85
180
合计
100
100
200
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
1.132
2.072
2.706
3.841
5.024
6.635
7.897
10.828
45岁以下
45岁以上
合计
闯红灯人数
15
25
40
未闯红灯人数
85
75
160
合计
100
100
200